Introduction

I have been fascinated with space since the first manned space flights when the whole world seemed to come to a standstill as we waited to see if the launch would be successful. So much has been learned and so much remains to be learned. I have to admit to being a Star Trek fan even though so much of what is shown is inaccurate. During my reading for this seminar, I have learned so much but realize how little I really know. I have chosen to limit my unit to a few simple formulas related to the study of the stars. These formulas involve distance, luminosity and velocity.

Most students in high school have a limited background in Astronomy. I want to broaden their exposure beyond our Solar System. In one unit, I cannot cover everything so I am limiting my unit to a few aspects of the stars. I have designed this unit for use in my PreCalculus classes. Just like me, my students are fascinated with space. How could they not be? We live in Florida not that far from the Kennedy Space Center. If the weather conditions are right, we can see the first minutes of a launch from our own backyards. They have also grown up with Star Trek and Star Wars. This seems the perfect hook to relate what we will learn to their interests. Too many times I hear "why are we doing this?" or "when will we ever use this?" I want them to see that Mathematics has a real purpose in the real world. At the same time, I want them to learn accurate information about the stars. While they are increasing their academic knowledge, I want them to realize that there are opportunities for them to be a part of the frontier that is still the study of the Universe. With a strong Mathematics and Science background, they have the opportunity to be pioneers and to make the next breakthrough to expand our knowledge base about the Universe.

Our seminar is covering a broad range of topics of interest to the fellows. This has given me an opportunity to build a broad base of general knowledge. As we ask questions and discuss topics in these areas of interest, I find useful information to help with my own unit. These are not questions that I would have thought to ask or would have thought would be helpful to my unit. I have also been able to ask questions that directly relate to the topics I will cover in my unit. The text recommended by Dr. Sofia has been particularly helpful as a starting point for my reading. While I am limiting my unit to the stars, I hope that my students will ask questions that go beyond the lessons I have prepared. With what I am learning in the seminar, I will be able to guide them to resources that can excite and challenge them.

This unit is designed for PreCalculus students. Most of these are juniors or seniors in high school. This unit could be used for Algebra 1 or Algebra 2 with some modifications. In elementary and middle school, their study has been limited to our Solar System and perhaps the Milky Way Galaxy. Even this will probably have been very limited in scope. In high school, most of these students will not have had courses that have units on Astronomy. They have taken Biology and Chemistry. Because we are on a 4 x 4 block schedule, they will be taking Physics before, during or after completion of my class. These students will have completed Algebra 1, Geometry and Algebra 2. My school is an ESOL Center. ESOL students are students whose second language is English. In my classes, I will have white and black students as well as students from several different countries. These ESOL students may be new to the country or have been here from a few months to a few years. Some of these students will have excellent Mathematics and Science backgrounds. This unit will be covering both Science curriculum and Mathematics curriculum. The writing component would also connect to the English/Language Arts curriculum.

Objectives

This unit is designed to teach Mathematics objectives relating to scientific notation, equation solving, the Pythagorean Theorem, units of measurement, writing formulas as ratios and converting from one unit of measurement to another. The Science objectives would include Astronomical measurement units and knowledge about stars related to distance, luminosity and velocity.

My students do not see Mathematics or Science as anything that will ever be of use to them. This will give them an opportunity to see both in the context of events happening in their world today. The success of the Deep Impact Spacecraft in hitting the Tempel 1 Comet is an event that I can use to show my students that there are still exciting challenges out there. You do not have to be an astronaut to be a part of space discovery. Science and Mathematics can be exciting activities that prepare them to be a part of the "final frontier".

Any study of Astronomy in a Physics class would be limited by the time available and the range of topics to be covered. By teaching this in a Mathematics class, students are exposed to the Mathematics and to the Astronomical knowledge in one situation. While I cannot teach to the same level as the Physics teacher, I can build interest and provide opportunities for them to explore on their own. There are many websites available where they can get accurate information at a level that is in their comfort zone.

They will increase their Mathematical skills by using them in a context that is different from what is normally found in the Mathematics classroom. By working with extremely large and extremely small numbers, they will have an opportunity to develop new techniques and confidence. Perhaps the next time a familiar skill is presented in an unfamiliar way, they will be more confident in attempting the work.

Standards

The student represents numbers in decimal or fraction form and in scientific notation.

The student understands the structure of standard measurement systems, both SI and customary, including unit conversions and dimensional analysis

The student evaluates and analyzes formulas and functions of many kinds, using pencil and paper and more advanced technology.

The student rounds numbers used in applications to an appropriate degree of accuracy.

The student uses the Pythagorean Theorem in many types of situations.

Overview

In this unit, we will review Mathematical skills that they have previously studied. We will study scientific notation. While they have learned this, they have not used it very often and are not particularly comfortable with using it. Because most numbers used in Astronomy are quite large or quite small, this is a skill that must be reviewed. Scientific notation rewrites these numbers as a number between 1 and 10 multiplied by a power of ten. The exponent of ten comes from how many places the decimal must be moved to get the number between 1 and 10. When there is no decimal written in the number, it is understood to be at the end of the number. For very large numbers, the decimal is moved to the left and the exponent is positive. With very small numbers, the decimal is moved to the right and the exponent is negative. For example, 345,000,000,000 would be written 3.45 x 10 ^{1 1} because the decimal at the end of the number was moved 11 places to the left. The small number .00000000000007468 would be written 7.468 x 10 ^{- 1 4} because the decimal at the beginning of the number was moved 14 places to the right.

When multiplying numbers written in scientific notation, the decimal numbers are multiplied together and the powers of ten are multiplied. When the powers of 10 are multiplied, the exponents are added. For example, 2.45 x 10 ^{1 2} x 3.67 x 10 ^{- 1 8} is 8.9915 x 10 ^{- 6}. It would be acceptable to round this answer to 8.99 x 10 ^{- 6}. This particular example was not hard to multiply by hand. I will also show students how to enter numbers of this type on the TI-83+ or TI-84 Graphing Calculators. The numbers between one and ten are entered from the keypad. To enter the powers of ten, the 10 is entered from the keypad. To enter the exponent, the ˆ key located in the right column directly above the ÷ key is pushed and the exponent is entered from the keypad. If the exponent is negative, the negative sign (-) is the key on the bottom row to the left of the "enter" key. Numbers are entered on the graphing calculator in the same order that they are written on the paper. When the answer is written, the multiplication symbol and the 10ˆ will be replaced with the letter E.

When dividing numbers written in scientific notation, the exponents will be subtracted. Remember that division can be written as a fraction. For example, 2.45 x 10 ^{1 2} / 3.67 x 10 ^{- 1 8} can be rewritten 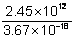. Divide the decimals by hand or by calculator. The result is .67 when rounded to two decimal places. When dividing the powers of 10, 12 – (-18) is 30. This gives .67 x 10 ^{3 0}. Rewrite .67 as 6.7 x 10 ^{- 1}. Multiplying by 10 ^{3 0} gives a final answer of 6.7 x 10 ^{2 9}. Depending on the numbers, it is usually better to do division with a calculator.

Formulas with multiple variables will be reviewed. In the past, they have rewritten formulas for a different variable than the one originally solved for. Again, this is something that they have done before but are not particularly comfortable doing. I will use formulas that the students are familiar with. To solve a formula for a different variable requires the same equation solving skills that are used in solving an equation in one variable. The formula for the area of a rectangle is A = bh. To solve for b, students will divide both sides by h. This yields 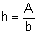. The formula for the area of a trapezoid is 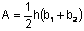. To solve for b ₁ involves more steps but works in the same manner. Multiply both sides by 2. Then divide both sides by h. This intermediate result is . Subtracting b ₂ from both sides gives the final result .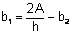

The Pythagorean Theorem will be reviewed. Of all the skills, this is the one that will be the most comfortable for them. When given a right triangle and the lengths for two of the sides, the 3 ^rd side can be found by using a ² + b ² = c ². Remember that c must be the side opposite the right angle. For the given right triangle, a = 5 m and c = 12 m. Using the Pythagorean Theorem, 5 ² + b ² = 12 ². Solving involves the same good equation solving skills that were used earlier and two more skills. First, 5 ² and 12 ² must be simplified to 25 and 144. Subtracting 25 from both sides results in b ² = 119. To find b requires taking the square root of both sides. Normally, I teach students to simplify radicals if possible. However, in this unit, it will be important to use a calculator and round to the appropriate number of decimal places for the particular problem. Because lengths of sides cannot be negative, we will write only the positive answer that b = 10.91 m. It is important to remind students that there are two answers found when taking a square root and that there are problems that will need both of these results. However, we are using the result that makes sense for our problem. It is important to review taking a square root on the graphing calculator. The square root symbol must be entered and then the 119. The square root symbol is not on a key. It is in yellow to the left above the x ² key. This is a second function for the calculator. To utilize the square root, push the yellow 2 ^nd key and then the x ² key. This places the √¯ symbol on the screen. Then enter the 119. One of the advantages of using a graphing calculator is that you see the problem you entered and the result. This is very helpful when you get a result that does not make sense with your problem. You can look to see if you entered it correctly.

We will look at taking two similar formulas and writing them as a ratio to create a simpler expression. This is a skill that will be useful in Calculus. For example, we have expressions for the areas of two circles. A ₁ = Πr ₁ ² and A ₂ = Πr ₂ ². Rewriting these as a ratio yields . Using good Algebra, the Π that is common to the top and bottom is eliminated giving an equation that is much easier to work with because the value of Π is no longer an issue. The new ratio is .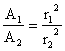

An extremely important part of this unit will be the review of units of measurement that they have previously used, and the introduction of new units of measurement. Metric units, especially meters and grams, will be reviewed. Students need to review the order from largest to smallest. I use the mnemonic King Henry Died __ drinking chocolate milk to help them remember that the order is Kilo_, Hecto_, Deka_, meter or gram, deci_, centi_, milli_. When moving from a smaller unit to a larger one, they are multiplying by a power of 10. When moving from a larger unit to a smaller one, they are dividing by a power of 10. Angle measurements in both degrees and radians will be used. It is important to remember that there are 360 degrees or 2Π radians in a complete circle. Conversions between customary units and metrics will need to be reviewed. These include:

1. n = 2.54 cm
2. t = .3048 m
3. i = 1.609 km
4. m/s = 2237mi/hr
5. i/hr = .447m/s

To work with new units unique to this study, we begin with 1 degree = 60 arcminutes

(60′ ) and 1 arcminute = 60 arcseconds (60″ ). The Astronomical Unit (AU) is a unit of length used primarily in measuring across our Solar System. It represents the average distance between Earth and the Sun.

1 AU = 1.496 x 10 ⁸ km or 8.317 light minutes or 92.96 million miles

When measuring units of length to the stars, two units of measurement are used. A light year is the distance light travels in one year.

1 ly = 9.46 x 10 ^{1 2} km or 63,240 AU or 6 trillion miles

Another unit of measure, the parsec, is the distance at which 1 AU subtends an angle of 1 arcsec. Sometimes, kiloparsecs and megaparsecs are used.

1. c = 3.09 x 10 ^{1 3} km = 3.26 ly
2. pc = 10 ³ pc
3. pc = 10 ⁶ pc

When working with very small distances, three units are important to know. They are the micrometer (mm), the nanometer (nm) and the angstrom (Å).

1. m = 10 ³ nm
2. m = 10 ^{- 9} m

The speed of light in a vacuum is represented by the letter c.

c = 3.00 x 10 ⁵ km/s = 3.00 x 10 ⁸ m/s = 1.86 x 10 ⁵ mi/s

Grams and solar masses are units used to express the mass of objects. For our study, those objects will be stars.

1. g = 1000 g
2. olar Mass = 1.99 x 10 ^{3 0} kg

To measure luminosity, we will use watts.

1 watt = 1 joule per second

A joule is the amount of energy in the motion of a 2 kilogram mass moving at a speed of 1 meter/second.

To convert from one unit of measurement to the other, we multiply by a fraction equivalent of 1. For example, to convert 524 miles into kilometers, 1 would be 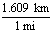. This comes from a conversion formula given previously. When this is multiplied, the miles units cancel and the final answer is 843.12 km. Remember that the unit you are converting to should be on top and the one you are converting from should be on the bottom.

Another very important subject for review is using correct units of measurement in an answer. Units of measurement should be defined at the beginning of a problem. When two identical units of measurement are multiplied, the answer is always squared. When three identical units of measurement are multiplied, the answer is cubed. For example, 2 m x 3 m = 6m ² and 12 cm x 5 cm x 3 cm = 180 cm ³.

The Universe has always fascinated man from the earliest times. As early as 280 B.C., Aristarchus developed a plan for determining the distance from the Earth to the Sun and to the Moon. (Freedman and Kaufmann, 2004. Unless otherwise noted, all Astronomical information comes from this source.) It was first believed that the Earth was the center of the Universe and that everything revolved around it. Then, the Sun was considered the center of the Universe. It is amazing how far Astronomy advanced without the sophisticated equipment available today. As mankind developed better techniques and more sophisticated equipment, we have come to understand that our Solar System is a very small part of a vast Universe. With all the talented Astronomers and all the high tech equipment, there are still so many things we do not know and other understandings that are no longer valid. As the Star Trek television series and movies always say "Space – The Final Frontier", space truly still is a frontier.

Stars have always held a sense of wonder for the smallest child to the oldest adult. There are about 6,000 stars that can be seen without any equipment. On any given night, there may be 3,000 visible stars in the dark part of the sky. Our location will determine how many of those are visible above the horizon. While they seem to be very close, they are really very far away. One ongoing work for some Astronomers is the measurement of the distance to these stars. In 1577, Tycho Brahe developed Astronomical instruments that were very sophisticated for his time, and took very accurate measurements of star and planet positions. In the last 100 years, advancements in technology have greatly enhanced our knowledge of the Universe.

The simplest way of measuring the distance to stars is stellar parallax. This was first successfully done in the 1800s. To understand the idea of parallax, use your hand extended in front of you. The background should have obvious differences. Cover one eye and then cover the other eye. Did your hand appear to stay in the same location? No, it did not. Our eyes work together to determine where our hand really is. To measure stars using stellar parallax requires two different observations of a star. These need to be done at two times when the Earth's orbits are the farthest apart. (See illustration 1). These measurements would be taken six months apart. The line of sight from the first observation forms one side of a skinny triangle. The line of sight from the second observation forms the second side of the triangle. The third side is the diameter of the Earth from one observation to the other. The height of this triangle is the distance to the star. Half of the diameter is the distance from the Earth to the Sun (1 Astronomical Unit). The parallax angle (p) that we need is half of the angle bisected by the height of the triangle. This triangle gives the equation 1 AU = dp where d is the distance to the star in parsecs and p is the measure of the parallax angle in arcseconds. Solving this equation for d gives the equation:

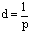
All stars have a parallax angle of less that 1 arcsecond. This is less than 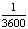of 1 degree.

When calculating the parallax angle, Astronomers must take into account the proper motion (Μ) of the star. Proper motion is how many arcseconds a star appears to move in a year on the celestial sphere. This motion is always in one direction. To determine proper motion requires three observations of the star. The third would be six months after the 2 ^nd when the Earth had returned to its original observation position. The distance between the original and final position of the star would be the proper motion for an entire year. Removing half this measure would give an accurate parallax measurement. (See illustration 2) (Seminar, 2005)

We cannot measure the parallax for stars that are very far from the Earth. To measure some of these, the parallax can be measured by satellites in space. For others, there are other methods to find the distance. However, it is still important for stars that are relatively close to have their distances measured using stellar parallax. This is essential for the other methods used in measuring distances to stars that are the farthest away. The result in parsecs can then be converted to light years or to kilometers using conversions given earlier. For calculating luminosity, we will need to convert it to meters.

When looking at the sky, one might think that the stars that are the brightest are the closest. This is not true. The brightest stars are often farther from us than some dimmer stars. Brightness has to do with thermonuclear reactions taking place within the star. Luminosity is how much energy from these reactions is emitted into space each second. If we know the brightness of the star and its distance, we can determine its luminosity. To do this, we use the Inverse-Square Law: where b is the brightness given in watts per meter squared, L is the luminosity in watts and d is the distance in meters. We may not know the exact value of the brightness but may know its brightest in relation to another star or to the Sun. To find luminosity, it is helpful to solve the equation for L. Multiplying both sides by 4Πd ² gives L = 4Πd ²b. Develop this equation for the star whose luminosity you want to find using the subscript 1. Develop the same equation for another star using the subscript 2. Create a ratio using the two equations.

The 4Πs cancel leaving a simpler equation.

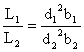
You will need to know the ratio of the brightness of the two stars. It is not necessary to know the actual value of the brightness for either star. You will also need the distance to each star or the ratio of their distances. Again, the result may not be the actual luminosity of either star but a ratio of the luminosity of one star to the other. In my class, we will be finding the luminosity ratio but, if 2 of the ratios are known, the third can always be found. For two stars with the same brightness, the one that is the farthest away must have a greater luminosity for us to be able to see it. A dimmer star that is closer would have less luminosity than a star that is brighter and farther away.

To the average person, stars appear to be stationary in the sky but this is not the case. They have space velocity. Space velocity tells the direction they are moving and the speed with which they are moving. To calculate space velocity, there are two components – tangential velocity and radial velocity. Tangential velocity is the movement across the sky or perpendicular to our line of sight. Radial velocity is movement in our direction or away from us or parallel to our line of sight.

Calculating tangential velocity requires us to know the proper motion and the distance to the star. To find tangential velocity (v _t), use the formula 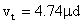where Μ is the proper motion measured in arcseconds and d is the distance measured in parsecs. The resulting velocity will be measured in kilometers per second.

Radial velocity (v _r) involves the measurement of wavelengths of spectral lines coming from the star. If the star is coming toward us, the shift is decreasing wavelength or blue-shifted. If the star is going away from us, the shift is increasing wavelength or red-shifted. The Doppler shift equation used to find radial velocity is:

where Λ is the star's wavelength in nanometers, Λ ₀ is the wavelength of the line at rest in the laboratory in nanometers and c is the speed of light in kilometers per second. Multiplying both sides by c gives the following equation:

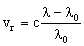
This velocity will also be measured in kilometers per second.

Tangential velocity and radial velocity are perpendicular to each other and form two sides of a right triangle. The space velocity is the hypotenuse of that right triangle. (See illustration 3) To find the space velocity, use the Pythagorean Theorem.

v ² = v _t ² + v _r ²

Taking the square root of both sides gives the formula:

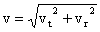
The results will be in kilometers per second.

Why should we be interested in distances to the stars, the luminosity of the stars or their velocity? There is so much still to learn about our Universe. The value of the Hubble Constant, the rate at which the Universe expands, is still not firmly established. It is considered to be approximately 71 km/s/megaparsec. Without an accurate value for this, we cannot get an accurate age for the Universe. We have the Hubble Telescope, the Chandra X-Ray Observatory and the Hipparcos Satellite in orbit allowing us to measure farther and with more accuracy the stars in distant galaxies. We have more powerful Earth-based telescopes and other Astronomical instruments to more accurately measure. Both Cepheids and Type Ia supernovae are used as "standard candles" to calculate distances to galaxies. (Finkbeiner, 1998)

Strategies

We are on a 4x4 block schedule. Students attend 4 classes each day for 90 minutes each. They earn 4 credits in the fall term and 4 in the spring term. I have my students 90 minutes per day for 90 days. These lessons will be taught in a student-centered classroom. The students will be working in groups of 3 or 4 students.

Our lesson plans are set up to include the standard, rationale, materials needed, the lesson layout, and the homework. Mathematics lessons are divided into three parts:

1) The Launch is where the topic for the day is introduced to the students. This can last from 15 to 30 minutes.

2) The Explore is where students work cooperatively on the activities of the day. The teacher circulates among the students to be sure that they are on task and not heading off in the wrong direction. The teacher does not tell the students how to do things but guides them by good questioning techniques back in the right direction. This section should last 45 – 60 minutes. In Mathematics classes, it is usually broken into sections. As students finish one type of activity, student presenters share their work with the class. Students can ask questions of the presenter, and the teacher can provide any needed clarifications and guide a summary of what the students have discovered. The teacher then sets the stage for the next activity, and the same procedure follows as with the first Explore activity. An explore period may have one or several Explore activities depending upon the length of time needed for each activity.

3) The Summary is when the teacher brings the class together as a large group to tie together and summarize all that has been accomplished during that period. This usually lasts 5 – 15 minutes.

I plan to begin with a KWL to find out what my students know about the stars, what misconceptions they have, and what they want (or think they want) to know. A short movie, "The Life Cycle of Stars" will be shown. We will do a review of the Mathematical skills needed prior to delving into our study of the stars.

I will introduce the study with an overview of how our knowledge of the stars has changed through the years, and what has been learned even as recently as the last few months. Each group will then be assigned a star whose distance can be determined using the parallax angle. They will be asked to calculate the distance to their star using a formula. These results will be converted from parsecs to light years to meters. Students will share their results with the rest of the class.

The distance results will be used to begin a discussion of brightness and luminosity. Students will be asked "which star do you think will be the brightest and why?" This discussion will lead into our next formula, the Inverse-Square Law. As a large group, we will solve the formula for L, and write it in terms of the star Sirius A using the subscript 2. They will write the formula for their stars using the subscript 1. Groups will be given the brightness ratio of their star and Sirius A. Using this, the distance to their star and the distance to Sirius A, they will determine the luminosity of their star as it relates to Sirius A. Students will share their results and be asked the question that started the lesson. This will lead to a summarizing discussion of luminosity and brightness.

To begin the next lesson, the question asked will be "do stars move?" This will lead into a discussion of space velocity. Each group will use the distance found for their star and the proper motion provided to find the tangential velocity of their star. Necessary information will be provided for groups to find the radial velocity. Students will use their results to find the space velocity for their star. Groups will share their results with the class. With our results, we will discuss how fast stars are moving, and in what direction.

As a concluding activity, a field trip will be taken to the Museum of Science and History Planetarium.

Each evening's assignment will be 5 to 6 problems relating to the type of problems done in class on that day. Students will also be asked to write about a topic of interest to them relating to the stars. These topics could include:

1. writing about a particular star or a particular type of star
2. writing about an Astronomer and his impact on Astronomy
3. writing about the impact of the Hubble Telescope, the Hipparcos Satellite, or the Chandra X-Ray Observatory, etc.
4. writing about a particular area of Astronomy that is of interest.
5. writing about an aspect of Astronomy that is still not understood
6. writing about an aspect of Astronomy that has not changed over a long period of time
7. writing about a particular galaxy

Lesson Plans

Lesson Plan 1

Standard

The student represents numbers in decimal or fraction form and in scientific notation.

The student understands the structure of standard measurement systems, both SI and customary, including unit conversions and dimensional analysis.

Rationale

For students to be successful in working with Astronomical formulas and data, it is necessary to review Mathematics skills and to introduce new units of measurement that will be required in our work with the stars.

Launch

KWL – Students will be asked to work in groups and brainstorm what they know about the stars. After the work period, students will share their understandings with the rest of the class. No corrections will be made by the teacher. This is just to find where the students are in terms of their background knowledge. Students will be asked to return to their groups and decide what it is they would really like to find out. After the work period, students will share these with the class. There will probably be topics raised that will not be included in our discussion. These might be good topics for the writing that will be the concluding assignment of this unit.

Show the movie "The Life Cycle of Stars". Students are to listen carefully and make note of any information in the movie that differs from the knowledge they shared during the KWL. After the movie, there will be a large group discussion where they will share what they learned.

Explore

The teacher will conduct a brief review of scientific notation including two example problems. In groups, the students will work on 5 sample problems involving very large and very small numbers. Two problems out of the 5, one a large number and one a small number, should be entered into the TI-83+ Graphing Calculator. They are asked to write down what the screen says for each problem, and compare it to their hand calculated results. Students should take no more than 5 - 10 minutes to accomplish this task. Individual students will present their work for each of these problems. As needed, the teacher will discuss the calculator use of the E in place of the 10ˆ.

Using the first two problems, the students (in groups) will be asked to first multiply, and then divide the numbers. Calculators may be used for dividing the decimal numbers. However, the powers of 10 should be done by hand. This should take no more than 5-10 minutes. Students will present their findings. If other students disagree with their results, they will need to show the correct procedure to the class.

Review converting from one metric unit to another. Introduce conversions from customary units to metric units. Explain that conversion from one unit to another is really just multiplying by one. Emphasize the importance of writing units with each number as the conversion is done so that the units that cancel can be seen. Students work in groups to solve 6 problems. Selected students present their work to the class. Discuss the importance of writing the correct unit of measurement for the answer. Emphasize that answers are not just numbers. They represent quantities that must be correctly identified.

Introduce Astronomical units. Discuss which units represent large quantities and which represent small units. Relate them to metric units to give a frame of reference. Note the importance of scientific notation in simplifying the work. Work examples with the students. Give each group a different problem to work on. Be sure all the new units of measurement are included. Each group will be the "experts" in presenting their problem to the class.

Summarize

Using a series of questions, summarize all the Mathematics that has been done.

Homework

Students will be given 10 problems to practice the skills reviewed and taught. Individual problems would incorporate more that one skill.

Lesson Plan 2

Standard

The student understands the structure of standard measurement systems, both SI and customary, including unit conversions and dimensional analysis

The student evaluates and analyzes formulas and functions of many kinds, using pencil and paper and more advanced technology.

The student rounds numbers used in applications to an appropriate degree of accuracy.

Rationale

Students need to understand that Astronomy is not a great mystery. Using simple Mathematical formulas, we can use data to calculate distances to stars.

Launch

Questions regarding the previous lesson and homework will be discussed.

What is the longest trip that you have ever been on? How long did it take you? When you look into the sky, how far away do the stars seem? Do you think you could travel to a star? Discuss briefly some history of attempts to calculate distance to stars. Explain stellar parallax. Do the hand activity to illustrate parallax. (See Overview) Using Illustration 1, derive the formula 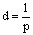. Explain the units of measurement. Discuss proper motion using Illustration 2.

Explore

Provide each group with a star and the measure of the parallax angle. Have them calculate the distance to their star. When each group is finished, ask them to convert their answer from parsecs to light years. Then have them convert their answer to kilometers and then to meters. Then have them convert from parsecs to miles. Work should be shown for the conversions as taught in Lesson 1.

Each group presents their work to the class. The data is collected into a chart on the white board or a transparency or a giant writing pad. This needs to be kept where it can be used for Lesson 3.

Summarize

How far was the closest star? How does that relate to the longest trip that you have ever taken? How long do you think it would take to reach the closest star? Do you think that could be done in your lifetime? Why or Why not?

Homework

Students will be given 5 stars and their parallax angle measurements. They will do the same work that they did in class including the unit conversions.

Lesson Plan 3

Standard

The student understands the structure of standard measurement systems, both SI and customary, including unit conversions and dimensional analysis

The student evaluates and analyzes formulas and functions of many kinds, using pencil and paper and more advanced technology.

The student rounds numbers used in applications to an appropriate degree of accuracy

Rationale

Students need to understand that Astronomy is not a great mystery. Using simple Mathematical formulas, we can use data to calculate the luminosity of one star in relation to another star whose brightness is known.

Launch

Students are given the formulas for the area of a rectangle and the area of a trapezoid. The first formula is to be solved for h. The second is to be solved for b ₂. The results are presented by different students. Discuss the importance of using good Algebra skills to complete this task.

Using the example of area of a circle from the Overview, illustrate how taking two equations and creating a ratio can result in a simpler equation.

Refer students to the chart created in class yesterday. Which of those stars do you think would be the brightest? Why do you think that? Groups share their results with the class and a data table is created.

Explore

Define luminosity and brightness. Present the Inverse-Square Law. Ask the students to solve the equation for L. See discussion in overview. Do not, however, explain that the brightest stars are the farthest away. This is a part of our discovery process. With the class, write the luminosity equation for L ₁ and for L ₂. Then write the ratio. What disappears from the two equations? This is the equation that will be used. Sirius A will be L ₁. Students will be given the distance to Sirius A and the brightness relationship between their star and Sirius A. Working in groups, they will find the luminosity relationship. Groups share their results with the class. Data is added to the chart begun on Day 2.

Summarize

Which star do you now know is the brightest of the stars you were assigned? Is it the closest star? What can you conclude? Why do you think this is true?

Homework

Provide the distance measurement and the brightness ratio of four stars. Students work as taught in class. Provide the brightness ratio and the luminosity ratio for a star and ask students to calculate the distance to the star. The reference star will be Sirius A for all these problems.

Cited Materials

Freedman, Roger A.and Kaufmann, William J. Universe. New York: W. H. Freeman and Company, 2005.

Finkbeiner, Ann K. "Cosmic Yardsticks." Sky and Telescope September, 1998: 38+

Teacher Bibliography

Bryant, Greg. "The Distant Night Sky." Sky and Telescope February, 2005: 63.

This article discusses distance measurement of objects in the sky.

Cowen, Ron. "Sizing up Small Stars." Science News December 14, 2002: 381.

This article discusses advancements allowing for accurate measurement of the size of small stars.

Croswell, Ken. "A Milestone in Fornax." Astronomy October, 1995: 42+.

This article discusses the continuing effort to estimate the Hubble constant.

Croswell, Ken. "How Far to Virgo?" Astronomy March, 1995: 48+.

This article also discusses the continuing effort to estimate the Hubble constant.

Finkbeiner, Ann K. "Cosmic Yardsticks." Sky and Telescope September, 1998: 38+.

This article discusses the use of Type Ia Supernovae as the standard candle for measuring the Hubble Constant.

Flowers, Charles. A Science Odyssey 100 Years of Discovery. William Morrow and Company, Inc. 1998.

This is a book that accompanied a PBS series. The first chapter in the book is a review of Astronomy in an easy to read form for high school students.

Freedman, Roger A.and Kaufmann, William J. Universe. New York: W. H. Freeman and Company, 2005.

This is my primary source for information on the Stars.

Ridpath, Ian. Stars and Planets. New York: Dorling Kindersley, 1998.

This is a book readily accessible to high school students with basic information about stars.

Schaff, Fred. "Savoring a Season of Dimmer Stars." Sky and Telescope November, 2004: 50.

This article is a discussion of dimmer stars.

Science News "X Rays Trace Fierce Stellar Winds." September 15, 2001: 174.

This is an article discussing stellar winds and how they heat up surrounding gas.

Science News "Galactic RAVE." June 14, 2003: 380.

This article discusses a project that will measure the movement of stars toward or away from the Earth.

Sky and Telescope "Cosmological Age Crisis Renewed?" August 1998: 21.

This is an article about measuring distances to stars.

Suits, Frank. "Astronomical Lengths with Simple Instruments." Sky and Telescope September 2004: 93+.

This is an article for students to show that amateurs can measure distances with limited accuracy without having to have expensive equipment.

Van Doren, Heather L. "Measure for Measure." The Sciences. July 2000: 9.

This is an article about the Chandra X-ray Observatory and its impact on distance measurement.

Websites

http://amazing-space.stsci.edu

This website provides educational materials for teachers and students.

http://hubblesite.org

This website provides access to pictures taken from the Hubble Telescope.

http://yahooligan.yahoo.com

This website provides educational materials for teachers and students. This is the source of the movie, "The Life Cycle of Stars" that will be used on Day 1.

Student Bibliography

Bryant, Greg. "The Distant Night Sky." Sky and Telescope February, 2005: 63.

This article discusses distance measurement of objects in the sky.

Cowen, Ron. "Sizing up Small Stars." Science News December 14, 2002: 381.

This article discusses advancements allowing for accurate measurement of the size of small stars.

Finkbeiner, Ann K. "Cosmic Yardsticks." Sky and Telescope September, 1998: 38+.

This article discusses the use of Type Ia Supernovae as the standard candle for measuring the Hubble Constant.

Flowers, Charles. A Science Odyssey 100 Years of Discovery. William Morrow and Company, Inc. 1998.

This is a book that accompanied a PBS series. The first chapter in the book is a review of Astronomy in an easy to read form for high school students.

Ridpath, Ian. Stars and Planets. New York: Dorling Kindersley, 1998.

This is a book readily accessible to high school students with basic information about stars.

Schaff, Fred. "Savoring a Season of Dimmer Stars." Sky and Telescope November, 2004: 50.

This article discusses dimmer stars.

Science News "X Rays Trace Fierce Stellar Winds." September 15, 2001: 174.

This is an article discussing stellar winds and how they heat up surrounding gas.

Science News "Galactic RAVE." June 14, 2003: 380.

This article discusses a project that will measure the movement of stars toward or away from the Earth.

Sky and Telescope "Cosmological Age Crisis Renewed?" August 1998: 21.

This is an article about measuring distances to stars.

Suits, Frank. "Astronomical Lengths with Simple Instruments." Sky and Telescope September 2004: 93+.

This is an article for students to show that amateurs can measure distances with limited accuracy without having to have expensive equipment.

Van Doren, Heather L. "Measure for Measure." The Sciences. July 2000: 9.

This is an article about the Chandra X-ray Observatory and its impact on distance measurement.

Websites

http://amazing-space.stsci.edu

This website provides educational materials for teachers and students.

http://hubblesite.org

This website provides access to pictures taken from the Hubble Telescope.

http://yahooligan.yahoo.com

This website provides educational materials for teachers and students. This is the source of the movie, "The Life Cycle of Stars" that will be used on Day 1.

Illustration 1

Illustration 2

Illustration 3