Introduction

We live in a world of patterns. They are all around us in everyday life, something that my first grade students notice and comment on quite frequently. When they recognize a pattern, or at least a perceived pattern by their definition, they become excited for successfully noticing a repeating motif or design. They will notice a red car go by, then a second red car, and then a blue car, and proudly say "It's a pattern, red, red, blue!" As a teacher, I am eager to harness this natural interest and excitement and use it as a teachable foundation. What comes next? How do you know that? Vocabulary and strategies for working with patterns will give my students greater ability to understand what they are already observing around them.

Edgewood Magnet School in New Haven, Connecticut is an arts magnet school, integrating the arts across the curriculum. Students in this environment are encouraged to use the strategies of observation, interpretation, and analysis to increase their thinking skills for every subject. Given this mission, the teachers and students in our school use unique and exciting approaches to "the basics" and work together to ensure that all students are included and learning. This educational approach supports the multiple intelligence theory and uses arts education as a means to assist students in improving their academic performance and enriching the lives.

I teach in a self-contained first grade classroom of about 25 students. Although these students come from various parts of the city, Edgewood is primarily a neighborhood school with a diverse population in grades kindergarten through the eighth grade. The students have a wide range of ethnicities, economical strata, and varying levels of academic and emotional strengths and weaknesses. The school has an enrollment of about 450 students with approximately 60% African-American, 12% Hispanic, and the remaining 29% Caucasian and Asian. About half of the students qualify for free or reduced lunch. Edgewood takes pride in a very high average daily attendance rate of 96%. This unit will align with the philosophy of our school.

Overview

The goal of this unit is to deepen students' understanding of how patterns work through manipulation of different materials and across the curriculum – art, music, literacy, and science, which, again, supports the mission of our school. It is intended to provide experiences for first grade students to learn about and understand patterns through exploration and discovery. Young students observe and experience the world sensorially. From this experience the child abstracts concepts and qualities of things in the environment. These concepts allow the child to make mental order of their world and function within that environment. This human tendency to make or identify order lends itself to the concept of pattern. The students' days are ordered, or to them, a pattern – they rise from sleep, go to school, eat meals in a certain sequence (breakfast, lunch and then dinner), go to sleep. Most certainly there are differences in each day but young children recognize the pattern of daily life and enjoy the knowledge of what comes next. Activities out of sequence, or order, can be upsetting or concerning to them – the pattern is incomplete or incorrect.

This cultural pattern of fundamentals of daily life can be brought to the classroom to use as a foundation to build the fundamentals of patterns. Patterns by definition are arrangements of things, such as objects, numbers, shapes, or sounds that are arranged following a rule or a set of rules. The members of the pattern are all related with each other by this specific rule. The pattern could be (potentially) infinite. Consider the set of numbers {2, 7, 12, 17, …} - this pattern has the rule of adding 5 to reach the next number, an infinite pattern. The other possibility is that the pattern may be finite, for example single digit odd numbers {1, 3, 5, 7, 9}. These examples of course would not be appropriate for younger students. Students in the early grades begin working with objects with attributes, such as size, shape, and color to generate repeating and growing patterns.

The current Mathematics curriculum in our school is ThinkMath published by Harcourt School Publishers. As the title suggests, the goal of this curriculum is for students to develop mastery by learning to think conceptually. We begin the year in first grade with two-dimensional figures and patterns, a review of their kindergarten skills of identifying figures, recognizing similarities and differences, and making patterns and designs. Aligning with our school requirements, this curriculum unit will extend this basic review to a more complete, conceptual understanding of how patterns are generated, ways they can grow, and how they repeat. ¹

Objectives

The National Council of Teachers of Mathematics supplies educators with standards and grade level expectations for our students. First graders are expected to be able to successfully sort, classify, and order objects by size, number, and other properties; recognize, describe, and extend patterns such as sequences of sounds and shapes or simple numeric patterns and translate from one representation to another; and analyze how both repeating and growing patterns are generated. With these focal points in mind, I would like to use the big idea of symmetry and wallpaper designs to guide my students through a more exciting, meaningful introduction to geometry and patterns. ²

Wallpaper groups categorize patterns by their symmetries. Simple differences may place similar patterns in different groups, while patterns that are very different in style, color, scale or orientation may belong to the same group. The symmetry of a pattern is a way of transforming the pattern so that the pattern looks exactly the same after the transformation, or as we say in First Grade, "Where is the repeat?" or "What comes next?"

The types of transformations that the students will begin to use and discuss include translation (shifting by one unit), rotation (turning clockwise or counterclockwise) and reflection (flipping on an axis). Often in primary mathematics instruction, students receive introductory exposure to these concepts. The purpose of this unit is to extend this exposure through more consistent and integrated activities to make this concept more accessible through daily morning activities, math centers, art projects, and music.

Symmetry on a Plane

Symmetries create patterns all around us and help us organize our world conceptually. Symmetric patterns happen in nature and are created by artists in many areas. Imagine a butterfly, whose wings are a reflection of each other. Or a snowflake that you can rotate 60 degrees at a time and it always looks the same. Look around at patterned rugs, tiled floors and walls, fabric, and wallpaper. Mathematics gives us a precise way to think about the subject of symmetry. The mathematical study of symmetry is carried out by looking at transformations of objects. The transformations to be discussed in this unit are translations, rotations, reflections and glide reflections of an object.

A symmetry of a figure is a transformation that leaves the figure invariant, meaning that taken as a whole, the object looks the same after the transformation as it did before, although individual points of the figure may be moved by the transformation. This section will discuss plane symmetries, those that take place on a flat plane. More specifically, we will discuss plane isometries: transformations that preserve distances. The transformations mentioned above are all isometries. Every plane isometry is one of these types. ³

Before working on a plane, first we should say what we mean by this term: we think of a plane to mean a two-dimensional set of points that goes on indefinitely in all directions and contains all the straight lines that connect any two points. Plane isometries involve moving all points around the plane so that their distances from each other remain the same. Plane isometries preserve all distances, and therefore all shapes, sizes, and angles. A pattern of points in the plane is symmetric if there is at least one non-trivial isometry that leaves the pattern unchanged. ("Non-trivial"means that it is not the identity: some points actually change position.) The term "isometry" comes from the Greek, iso meaning "same" and metry meaning "measurement." Another term to use to discuss these isometries is rigid motions of the plane. ⁴

A translation means to move an object across the plane by a certain distance and in a certain direction. This is the simplest isometry, as everything is moved by the same amount and in the same direction. Every line segment is sent to a segment of the same length, and parallel to the original segment.

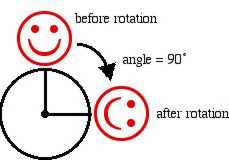
A rotation fixes one point and everything rotates by the same amount through the same angle around that point.

To reflect an object means to produce its mirror image over a fixed line, also called the axis of reflection.

Glide reflection combines a reflection along a mirror, or axis, with a translation along the direction of the mirror line.

Again, a figure, picture, or pattern is symmetric if there is at least one symmetry that leaves the figure unchanged. For example if we use the letters in ATOYOTA, we will form a symmetric pattern. By drawing a vertical line through the center of the "Y" and then reflecting the entire phrase across the line, the left side becomes the right side and vice versa. Additionally, each letter in this pattern is individually symmetric across a vertical midline.

The identity map, or doing nothing, leaving every point exactly where it is, is also an isometry. We can't do without the identity, it is very important, but clearly, the identity will preserve every figure in the plane, so having the identity as a symmetry is not an interesting property. Therefore, when discussing symmetry, we only say that an object is symmetric if there is a non-identity (which we will also call non-trivial) transformation that preserves it.

A further example of symmetry comes from the idea of drawing a figure of a person and copying it to make a line of people going in both directions – this is a symmetric pattern. You can translate the whole group ahead one person, and the line will look the same. This pattern has infinite number of symmetries since you can translate forward by one person, two persons, or three persons or backward by the same numbers, or even by no people. We say that this pattern has translational symmetry.

The term fundamental domain is used to define a part of the pattern that can be repeated to generate the whole pattern, without overlap. If we apply all the symmetry operations of the pattern to this fundamental domain, we will generate what we see as the pattern. The symmetries of a pattern get applied to the whole pattern, but you can break the pattern up into copies of the fundamental domain, each produced by applying exactly one of the symmetries to that domain. Also, keep in mind that fundamental domains are not unique.

Finite Figures

Finite figures, unlike lines, do not go on forever. They are shapes which have no translational symmetry. The shapes discussed in this unit will be regular polygons, defined as a shape with all its sides equal and all its angles equal. Regular polygons have reflections and rotations as symmetries – they have reflectional symmetry, and also rotational symmetry.

Symmetry Classification of quadrilaterals

Square – 8 symmetries – the regular quadrilateral

Rectangle and rhombus – 4 symmetries

Parallelogram, kite and isosceles trapezoid – 2 symmetries

Frieze Patterns

A frieze, or strip pattern, is a repeating pattern with translational symmetry in one direction. Additionally, the repeating patterns may have rotational, reflectional, or glide reflectional symmetry. Often these frieze patterns are seen as decorative borders in art and architecture around the world. And mathematically, it turns out, there are seven classes of frieze patterns that are generated by the isometries mentioned. They consist of the following structures:

• Class I – translations only
• Class II – translations and horizontal reflection
• Class III – translations and vertical reflections
• Class IV – translation and rotations by 180°
• Class V – contains all possible types of symmetries of a strip – translations, horizontal and vertical reflections and rotations by 180 ^o
• Class VI – translation and glide reflections and translations
• Class VII – glide reflections, translations and rotations by 180°

To help visualize these isometries, John Conway, a noted mathematician at Princeton University, developed a whimsical, yet accessible method of understanding these classes of frieze patterns. By using the idea of our footsteps, we can call each class by a corresponding move that we might make ourselves with our feet (or a single foot in two of the Classes). These movements identify the repeat or fundamental domain. ⁵

• Class I – Hop – one foot moving forward
• Class II – Jump – two feet together jumping forward
• Class III – Sidle – toes facing each other to heels facing each other
• Class IV – Spinning Hop – one foot to generate the rotation and the translation
• Class V - Spinning Jump – two feet together, spin around and forward
• Class VI – Step – basic walking forward
• Class VII – Spinning Sidle – heels facing each other, a spinning hop forward

Wallpaper Groups

Wallpaper patterns result when symmetrical repetition takes place in two directions, thus forming a two-dimensional pattern that covers the plane with no gaps or overlaps. Although it seems that there would be a limitless variety of repeating patterns, it turns out that there are only 17 systems which mathematicians classify as symmetry groups. E.S. Fedorov published his proof of only 17 possibilities in 1891, but it appeared only in Russia. In 1924, George Polya published his paper, "Uber die Analogie der Kristallsymmetrie in der Ebene," translated "On the analogy of crystal symmetry in the plane." This is important to note because it reflects that fact that wallpaper patterns are related to the crystals studied by chemists. His paper gave an example of each wallpaper pattern and these examples were an inspiration for the Dutch artist M.C. Escher, famous for his intriguing drawings that are examples of these symmetries.

Each symmetry involves a combination of transformations on the plane. To determine how to categorize or organize these different wallpaper patterns we can ask a series of questions about the isometries. The answers to these questions will generate a way to think about the organization of the patterns.

First we begin with the question "What order of rotations are there?" To answer this, first we must recognize that there can be rotations of orders 1, 2, 3, 4, and 6 in the wallpaper groups, and these are the only possibilities. This is called the "crytallographic restriction". Next, we ask are there any reflections or glide reflections? If so, is the lattice rectangular or rhombic (with respect to the axis of reflection)? If rectangular, are there reflections (as opposed to glide reflections?) If so, is there an axis of reflection through a point of maximal rotation? Finally, if the maximal order of rotation is three, you have to look carefully: there are two choices, reflection through the midpoints or reflection through the axes. The following table shows the number of symmetry types having some of these properties.

Although to teach this curriculum unit, this level of detail is beyond the scope of the students' learning, it is a desirable foundation for the instructor to have for preparing activities and relaying the concept properly and accurately.

Teaching Strategies

The approaches for this curriculum unit will vary to reflect the learning styles of all students. Included will be:

Experiential Learning: The major strategy for this unit is to engage the students in hands-on learning. I want them to be actively participating as mathematics discoverers, not observing a demonstration by the teacher or looking at examples in books. The activities will be designed to be exploratory for the students so they are engaged in the enjoyment of the process as well as the product. A wide range and variety of mathematics and art materials will be included in the exploration and design. This will also include science activities and musical experiences with patterns.

Differentiated Instruction: Lessons and activities will be targeted to maximize learning. The students will use a variety of approaches, working sometimes individually and sometimes in small groups, determined by the complexity of the activity. Because these are young children with variance in levels and background, guidance and pacing will need to be closely monitored. Mathematics concepts need to be based in concrete experiences.

Cooperative Learning: The students will be given opportunities to work as cooperative groups to complete assignments and activities. This strategy will allow students to work collaboratively taking on various roles necessary to complete the work, with a focus on success for all. A culminating activity will include groups designing wallpaper that will be displayed in our classroom, with descriptions of types of transformations included in the design.

Classroom Activities

1. Introductory Activity Ideas for Integrated Learning

The introduction of pattern recognition will begin with read-alouds from the collection of student resources, reading first Patterns – Math Counts by Henry Arthur Pluckrose. The pictures show basic objects in our lives and will promote discussion. The text is simple and straightforward and the students will begin to develop vocabulary for discussing patterns. Include in this set of terms location words – before, after, beside, up, down; attribute words – colors, size, shapes.

Each day will include one or more of these activities to allow for repeated experience. They can take place during the morning meeting on the rug, preparing for a transition, and as a beginning component to the daily math lesson.

Objective: The students will practice generating patterns through a variety of opportunities for experiential learning.

Procedure: Organize the students in groups or a circle. Choose an activity to practice for approximately 5 minutes.

Clap patterns - fast, fast, slow, fast, fast, slow (AAB pattern)

Actions - hop, hop, clap, clap, hop, hop, clap, clap (AABB pattern)

Drama activities - swirl arms like the wind, arms up like the sunshine as you say: windy,

windy, sunshine; windy, windy, sunshine

Line up at the door in patterns - boy, girl, boy, girl (AB pattern) Let the students recognize that these patterns could continue forever, or are examples of frieze patterns.

Introduce and practice translations – line students up and step forward one giant step, sideways left one giant step, sideways one giant step, backwards one giant step – notice we are all still next to the same students

Introduce and practice rotations – stand and face one direction, turn 90 degrees, turn again 90 degrees, turn again 90 degrees, and again, back to the "identity", or original position. Repeat only reverse the direction. Come back to original position.

Introduce and practice reflections – stand facing another student and repeat arm, leg and body motions to show reflections

2. Math Center Activities

Objectives: The students will use hands-on experiences to understand pattern and sequence, recognizing the fundamental domain and demonstrating the ability to generate the repeat.

Materials: pattern blocks, counting bears, attribute blocks, crayons, pencils, objects from nature (acorns, shells, pebbles, leaves), coins,

Procedure: The math center activities will allow the student to explore. Each activity should include appropriate materials contained in baskets or tubs. Students may work in groups or singly to show their knowledge of patterns. The students should have sufficient quantity of the materials to repeat the pattern several times. These activities should take about 10 minutes and there should be opportunities for each student to participate in all the centers at some point.

1. Create color patterns with materials – example: red crayon, blue crayon, red crayon, blue crayon. Change materials each day or rotation of centers to objects such as colored counting bears, pine cones and acorns, shells, etc.
2. Put pattern blocks in the pocket chart or on mats – example: hexagon, hexagon, triangle, hexagon, hexagon, triangle. Provide exploration tubs of pattern blocks to allow students to create frieze patterns and to begin to explore wallpaper patterns. There should be exploration and discovery occurring.
3. Diagrams or drawings – example: draw big apple, big apple, small apple; repeat. This activity should include simple, recognizable items or shapes for the drawing. The center should include only the drawing and writing materials needed to complete the pattern - any additional choices may be confusing. If the pattern includes the colors red and green, offer only those two colors.
4. Letters and words - put letters or words in the pocket chart or on mats. AA BB, AA BB or cat, cat, dog; cat, cat, dog

Assessment: Students will share with the teacher and/or the class their patterns, using descriptive words to show understanding.

3. Exploratory Activities

Objective: The students will use a variety of materials to examine and generate a variety of strip or wallpaper patterns with those materials.

Procedure: Read aloud Lots and Lots of Zebra Stripes: Patterns in Nature by Stephen Swinburne. Engage the students to discuss the patterns they notice on each page. Encourage them to use descriptive words to explain what they see. How do they know it is a pattern? What would come next?

The students should work in teams of two for these activities. The students will work together trading roles as "designer" and "repeater". This should be approached as cooperative learning, allowing for exploration and student interaction with limited involvement of the teacher. The following

a. Create their own patterns at various difficulty levels use a selection of cutout shapes of construction paper (for example, from an Ellison or other die cut machine)

red, blue, red, blue...

• red, blue, yellow,…
• red, red, blue, red, red, blue....
• red, blue, yellow, yellow, yellow…

b. Copy patterns that others have made

c. Extend patterns that others have started

d. Tell what is missing if part of a pattern is hidden

For activities a, b, and c – The students can use pattern blocks, cutouts, small objects, etc. This should be differentiated for the students to create patterns based on their level of understanding so including a small variety of choices would be appropriate. Keep the collections of objects in separate container or tubs to encourage success and not confusion. Each pattern activity should use only one tub at a time. Cooperative learning should occur as students work together to create their own patterns.

Objective: The students will recognize patterns exist naturally in our environment.

Materials – chart paper, markers, read aloud book

Procedure: Read aloud Patterns Everywhere. Students will recognize the objects and places in the book. Use this as a basis for the students to:

a. Compare and talk about patterns that arise from their daily experiences to understand that our lives have patterns. This is a good opportunity to share sequencing. An example may be how we brush our teeth and discuss the order of events, first the toothbrush, then the toothpaste, brushing, rinsing, etc. If the pattern has changes, then the activity would not work the same way. Have the students continue with other patterns or sequences of activity and discuss the need for order for that particular activity

b. Recognize patterns in the environment – example: fence posts: short, tall, short, tall... Use the classroom (windows, desks), hallway (doorways, tile), school grounds (playground equipment) and generated an on-going list to keep posted in the classroom

c. Use patterns to describe the world around them and to solve problems – discuss how "knowing what comes next" helps understand order in the world (patterns in the tile with no gaps or overlaps keeps the floor level, windows would be missing if the patterns are not complete, have students discover other patterns and problems they can solve and keep an on-going list of solutions they discover posted in the classroom.

d. Identify a pattern – describing the pattern, what they see and what makes it a pattern. Encourage the use of vocabulary that is clear. Keep an on-going list of vocabulary that the students use for describing.

4. Culminating Activity

The class will create a wallpaper design for the classroom using handprints. This will require a large paper from a roll, enough to cover an area on an available wall or bulletin board. Working together, the class and teacher will determine design and colors. Although the wallpaper will be the student's work, it will be necessary for the teacher to be quite involved with the painting process. The teacher will paint the hands (one at a time!) and help the students locate the correct spot for their handprint (color and orientation). As the teacher is working one on one with the student, on-going assessment can take place. Questions such as "What color will you need?" and "Where should you add your handprint?" will provide the teacher with a level of each student's understanding.

Appendix - Implementing National Standards

Algebra Standard

In accordance with the National Council of Teachers of Mathematics Standards and Expectations for First Grade, after completing this unit, the students will be able sort, classify, and order objects by size, number, and other properties; recognize, describe, and extend patterns such as sequences of sounds and shapes or simple numeric patterns and translate from one representation to another; and analyze how both repeating and growing patterns are generated.