- Login
- Home
- About the Initiative
-
Curricular Resources
- Topical Index of Curriculum Units
- View Topical Index of Curriculum Units
- Search Curricular Resources
- View Volumes of Curriculum Units from National Seminars
- Find Curriculum Units Written in Seminars Led by Yale Faculty
- Find Curriculum Units Written by Teachers in National Seminars
- Browse Curriculum Units Developed in Teachers Institutes
- On Common Ground
- Publications
- League of Institutes
- Video Programs
- Contact
Have a suggestion to improve this page?
To leave a general comment about our Web site, please click here
Putting the Pieces Together
byElwanda ButlerIntroduction
Why are we doing this? or Why do we have to do this? These are questions that my third graders ask before starting a lesson. Students at this age are very curious. They also want immediate feedback. As a teacher, it is extremely important for me to explain the relevance of all assigned tasks. Students should know the reasons why they learn. Once they understand the importance of learning, they might even study more. I connect every aspect of learning to the real world. The curriculum must be made meaningful and engaging to the students. Putting the Pieces Together is a math unit designed to keep students actively engaged. Students learn about line of symmetry as well as the different types of symmetry, such as transformations, reflections, and glides. They will have fun studying frieze patterns. After this unit, students will look for symmetry everywhere.
I teach third grade in an urban Chicago Public School. My school serves about 248 students in grades Kindergarten to Eighth. 100 percent of the students are African-Americans. About 87 percent of the students receive free or reduced lunch. 100 percent of the students come from low income families. Many of our students are faced with obstacles at home and in their neighborhood. So they come to school not only to learn but for comfort and to be safe. We are faced with many challenges. According to the state tests, about 42 percent of the students are reading at or above grade level. About 52 percent of the students are meeting or exceeding state standards in math. As a professional learning community, we are working smart to maximize instruction for all our students. We strive to educate, support and nurture students. Academic programs include an after-school program partnered with Newton Learning, which provides additional assistance in math and science for students in grades 1-8. To enhance education, partnerships with external organizations, such as universities, businesses, and community centers have been established. These organizations provide additional assistance to students, parents, and teachers. The school staff frequently analyzes data to inform instructional decisions. The data-based decisions allow teachers to take a closer look at curriculum and instruction used to increase student achievement.
In my class of about 30 third graders, the academic abilities in reading and math range from beginning second grade to the fourth grade level. I differentiate instruction on a daily basis to meet the need of all the students. I use guided reading and math groups. I incorporate student interest in the lessons. I make sure connections are made across the curriculum; integrate different subject areas by finding common themes. In order to incorporate students' different learning styles into lessons, I spend a great deal of time planning and attending professional development; to stay knowledgeable of current techniques/strategies. In my classroom, I establish a learning community at the beginning of the school year. We work hard, we learn hard, and think even harder.
Overview
This unit is created to teach third graders about the mathematical concept of symmetry. The unit can be adapted for other grade levels. Students get the opportunity to learn about symmetry over the course of 5 weeks. Instruction is given in whole and small group settings. Students work in cooperative groups, pairs, and on their own. Each lesson takes about 45 minutes to complete. Students receive a hands-on math experience. I integrate math with language arts and art. For the language arts component, we read math related picture books. Students discuss the books and apply learned information to the math lessons. The books provide additional background information for the students. Many of my students come with limited background information. I expose students with this information; to ensure they have a basic understanding of the concepts before starting the unit. During math lessons, language arts are incorporated by discussing word problems in class, asking such questions as, what is this problem asking, how you know, and comparing problems. Art is immersed throughout the unit; students create different symmetrical designs/projects.
Students learn how symmetry is all around us. Students look at symmetry through nature (insects, flowers, and trees), architecture, and art. Students get the opportunity to take a look around the city of Chicago; and identify symmetrical objects. As they walk around areas in Chicago, I ask questions about symmetry and the type of patterns they see on the buildings. During this walk, students sketch objects and patterns. In this unit, third graders are challenged to think beyond understanding lines of symmetry. We study the seven different types of frieze patterns. As we look at the frieze patterns, we learn about translations, reflections, rotations (only by 180 degrees), and glide reflections. Students reflect, write, and explain their thinking.
This unit incorporates real life experiences with math. Students use resources from outside, home, and school for some of the activities. They talk about how math connects to the world. These experiences help students see the value of the math they are studying. By linking a math concept to something relevant in a student's life, you can help increase a student's interest in the topic, and help make math more meaningful. When students are interested, the levels of motivation increase.
Rationale
Geometry is important for students to know because it provides methods of reasoning and solving problems. The world is made up of geometrical objects and figures. (1) Symmetry is a part of geometry that is found all around us. Symmetry is found in a variety of things, such as clothes, flags, and buildings. Many of our jobs contain components of understanding math as well as using geometry. This statement answers the question: Why do we need to do this? You cannot get away from math. It is everywhere! Math is unavoidable. It's a deeply important thing. Without math, there would be no science, no music, and no art. Math is part of all of those things. This unit will convince my students of this universal truth.
In the state of Illinois, third graders are required to learn about the strand of geometry. Students must know how to compare geometric figures and determine their properties including i) when two lines are parallel, ii) when two lines are perpendicular, iii) when two figures or configurations are congruent, and iv) when a figure has a line of symmetry. Students will begin to see the power and utility that math brings to expressing, understanding and solving problems in diverse settings beyond the classroom. (1)
The study of geometry including symmetry is taught in my school's Everyday Math Curriculum, a research based curriculum that connects math to real world applications. It also integrates mathematics into other subject areas so math becomes part of ongoing classroom and external events. Since the curriculum is spiraled, students learn many concepts at once. They are constantly revisiting some of the concepts. Third graders using Everyday Math are supposed to learn about two-dimensional symmetric shapes or designs; locate multiple lines of symmetry in a two-dimensional shape, and create symmetric shapes. Students apply Transformations and Symmetry in Geometric Situations. (2) However, we only have a few symmetry lessons in the curriculum for third graders. The data at my school shows that our students' geometry scores need to improve. So as a teacher, I must bring in additional resources to expand the geometry section of the text. The resources must provide meaningful opportunities for the students to learn and retain the information.
The majority of my students enter third grade with little knowledge of geometry. They can tell you the basic names of polygons, such as rectangles, triangles, and squares. Some students have a difficult time explaining the number of sides and vertices on certain polygons. Identifying patterns also is a difficult task for some students. They need concrete examples/models to grasp the concept. At the beginning of third grade, the term symmetry is new to most of the students. They never heard of symmetry or have forgotten what symmetry means. I know that this topic is covered briefly towards the end of second grade.
According to the National Council for Teachers of Mathematics, "Students enter grade 3 with an interest in learning mathematics. Nearly three-quarters of U.S. fourth graders report liking mathematics, seeing it as practical and important. If mathematics continues to be seen as interesting and understandable, students will remain engaged. If learning becomes simply a process of mimicking and memorizing, students' interest is likely to diminish." (3)
As teachers we must provide learning opportunities in which students can inquire, think, and apply math to real world situations. Students at all grade levels need to be challenged, but not to the point of frustration. Adding a touch of fun in math, will keep most students actively engaged and motivated to learn math.
To help them compete with the world, I want to equip my students with the necessary math skills. As an intermediate teacher, I want to provide students with a solid math foundation. This foundation helps students make sense of the world around; students will be ready for the advancements in technology. "Through math, students learn to reason, to connect ideas, and to think logically. Math is more than the rules and operations we learned in school." Math is about making connections and seeing relationships in everything we do. (4)
I want my students to have conversations and not be afraid to tackle a math problem/concept. Some adults do not like math based on experiences they have had in elementary/high school; math is feared by them. I do not want my students to be categorized as these adults. Students need to have fun and learn at the same time.
Putting the Pieces Together is a curriculum unit that students will enjoy; the curriculum provides an unforgettable learning experience. Students will learn the state required math goals in addition to other ways to think about math.
Objectives
At the end of the unit, students will be able to do the following:
- Identify lines of symmetry found in different objects.
- Find the smallest translational symmetry in a frieze pattern.
- Identify glide reflection symmetries of frieze pattern.
- Tell the difference between the types of symmetry, such as rotations, reflections, slides, and glide reflections.
- Identify the different types of frieze patterns.
- Explain why the frieze patterns are different.
- Create designs that contain symmetry.
- Effectively communicate their knowledge of symmetry to others.
This unit begins with a pre-assessment to find out what the students already know about symmetry. The pre-assessment evaluates basic knowledge of symmetry. The students will have to determine how many lines of symmetry an object or shape has. They will have to tell if a given object made a reflection, rotation, or translation in a given picture. I will compare the pre-assessment data to the post assessment at the end of the unit. The post test will look at similar information. This will let me know if the students have learned the skills/concepts. A rubric will be used to score final projects. The criteria on the rubric will consist of the unit objectives. Throughout the unit students keep a math journal to take notes, reflect, and record vocabulary words.
Background Information
Symmetry is an important part of geometry, nature, and shapes. It creates patterns that help us organize our world conceptually. We see symmetry every day but often don't realize it. (5)
There are several types of symmetry.
Reflection: Reflection in a line moves each point to a point on the other side of the line, and at the same distance from the line as the original point; and the line connecting the point and its reflection is perpendicular to the line of reflection. A reflection of an object produces a mirror image of the object.
Reflection Symmetry: A characteristic of a figure or design that is unchanged under reflection in some line. The line is then called a line of symmetry of the figure.
Line of Symmetry: A line that divides a figure or design into halves that are the mirror images of each other.
Lines of symmetry are easiest to identify when they are vertical or horizontal. However, a line of symmetry can be oriented in any direction.
Some examples are shown below.

Rotation: A rotation around a given point as the center moves every point on a circle around the center, through a fixed angle.
Rotational Symmetry: Is the characteristic of a figure or design that will coincide with (look the same as) itself after being turned less than 360 degrees (which is a full turn). (6)
Translation: Is a motion that slides a figure or design in a fixed direction. (6) A translation is defined by an oriented line segment. A translation moves every point the same distance, which is the length of the line segment defining the translation. A translation will move an arbitrary line segment to a segment of the same length, and parallel to the original segment. (7)
Translational Symmetry: Is the characteristic of a figure being preserved by a translation.
Glide Reflection: Is the result of reflection in a straight line, followed by sliding in a direction parallel to that line. (6)
Glide Reflection Symmetry: Is the characteristic of a figure being preserved by a glide reflection.
Frieze Pattern: Design that exhibits translational symmetry in just one fixed direction. Frieze patterns may also have reflection symmetry, glide translation symmetry, or rotation symmetry (180 o rotations only). (6) These patterns can also be thought of as the idealization of a repetitive motif on the frieze of a building. Frieze patterns can be found in the repeating decorations around the rims of vases, bowls, and cups. (7)
Frieze Group Classifications: There are seven classes of frieze groups. John Conway, a mathematician, has described each of the seven frieze groups in terms of footprint movements: Hop, Jump, Sidle, Spinning Hop, Spinning Jump, Step, and Spinning Sidle. (7)
Pattern 1: (Hop) Translations Only - All the points in the plane move in the same direction/distance.

Pattern 2: (Jump) Translations and reflection across the central axis of the pattern.

Pattern 3: (Sidle) Translation with Reflection in lines perpendicular to the translation direction. (This is often just called a vertical reflection.) In this particular group, all of the points in the plane are reflected across a vertical mirror. Together with the translations, this implies that the pattern is symmetric in a family of vertical mirrors spaced at one half of the minimum translation distance. (7)
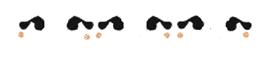
Pattern 4: (Spinning Hop) Translation and rotation around the point on translation axis. Again, when we multiply one rotation by translations, we get a collection of rotational centers spaced half as far apart as the minimum translation distance.

Pattern 5: (Spinning Jump) Translations with both Vertical and Horizontal Reflections (Therefore also rotations). The centers of rotation are the intersections of the vertical axes of reflection with the axis of horizontal reflection.

Patterns 6 and 7 are the most difficult. These patterns contain translations and glide reflections. They are the subtlest from the point of view of symmetry. (7)
Pattern 6: (Step) Glide Reflections- This particular group takes all points in a plane and reflects them over a line at the same time that it translates them along the line. Therefore a step pattern is generated by a single glide reflection. The square (= two-fold repeat) of this motion is a pure translation, in the same direction, of double the displacement.

Pattern 7: (Spinning Sidle) This pattern is generated by a glide reflection, together with vertical reflections and rotations. Unlike pattern 5, the centers of rotation do not lie on the vertical axes of reflection. Instead, they are halfway between these axes.

Strategies
This unit integrates math, language arts, and art. The activities are differentiated to meet the needs of all my students. Throughout the unit, I read aloud all directions and have students repeat the directions. Some students will only be required to learn three frieze patterns out of the seven. The assessments and projects can be easily modified for the students. When it comes to addressing students who need interventions, differentiated strategies may improve learning.
The strategies used during the lesson will allow students to learn about symmetry and how it connects to the real world. Students take ownership of the activities. They learn not only from the teacher, but also from peers. Students lead some of the discussions throughout the unit. As I integrate the unit with literature, I introduce picture books. Students will read Let's Fly a Kite by Stuart Murphy. This story gives many colorful examples of symmetrical kites. After the book is read aloud, I lead a discussion and ask questions about the book. The questions will focus on the topic of symmetry. I talk about the illustrations and find out how many objects have lines of symmetry. We will also take a look at another book called Symmetry (My Path to Math) by Lynn Peppas. This non fiction book presents real life examples of finding symmetry all around us. After reading this book, students start to notice symmetry everywhere. Using picture books help students remember the information when it is time to talk about math.
The following strategies are used: Charts/ Graphic Organizers, Manipulatives, Journaling, and Student Ownership.
Charts/ Graphic Organizers
Before I start the unit, I activate students' prior knowledge to find out what they already know about symmetry. I create a K (Know)-W (Want to Learn)-L (Learned) chart about symmetry. Students will list what they already know about the concept. If students have misconceptions about symmetry, they will be addressed. One misconception that some students have is that all objects have symmetry. On the chart, students list what they want to learn. After the unit is complete, students will list what they have learned. This chart will be displayed throughout the unit. Each student has a copy of the KWL chart. As we go through the unit, the students will add information on the chart. This strategy is intended to actively involve students. The connection between prior knowledge and the information presented in the math unit is made real. I will guide students through this process to think of symmetry questions they need and want to have answered. During this time, I will get an idea of who already knows about geometry and symmetry.
We use vocabulary graphic organizer/charts to define and illustrate our math terms. Every time the students learn a new term, they complete an organizer. These organizers are posted in class; they create a print rich math environment. Students can also create their own organizers. The organizers are used as study guides. It is extremely important to stress math vocabulary because students need this information for future assignments and assessments.
Journaling
Math journal writing is a useful strategy. Each student receives a math journal. Students write after each activity/lesson daily. They explain what they learn and how they learned the math topic. The students are required to use illustrations in their journals. The journal time improves writing and math skills. Throughout the unit, I check journals to make sure students understand the materials. The journals can serve as a way to assess the students. In order to assess the journal writing, I let the students know in advance what I will assess for that day. For example, I might assess how students draw a particular frieze pattern. The journal writing provides students with opportunities to take ownership of their learning. Students use their journals as an additional class resource. If they forget math information or facts, they look back in the journal. Many students like to read aloud and share their journals with peers. Students are allowed to take their journal home. When students find symmetrical objects at home or in their neighborhood, they are allowed to record/sketch this information in the journals. The parents also can look in the journal to see what is going on in math.
Manipulatives
Math manipulatives are useful instructional aids that I use as part of the teaching strategies. Manipulatives help students explore, discover, sort, and assess. (2) I start many of the activities in this unit with manipulatives. For one of the lessons in this unit, I provide students with paper polygons to count the sides and fold to identify the lines of symmetry. Students also use cut out alphabets to find out which letters are symmetrical. They find out how many letters of their name are symmetrical as well. The students challenge each other to see who has the most letters. Using manipulatives help my students understand the concept faster than using just paper and pencil. I have a lot of students who need concrete examples. They need to be able to feel objects to better process the information. It is important to have the manipulatives organized and ready for the students. Students need time to touch and observe the objects before the lesson starts. If they do not get this time, they will focus more on the objects during the instruction time.
During this unit, students get the opportunity to go on a walk around the city. As they walk, they gather symmetrical objects, such as flowers, leaves, and insects. I allow one student to take pictures of the objects they see, especially the insects or things we can not bring inside the class. This experience brings life into the classroom. While we walk, students look at buildings in Chicago. They search for frieze patterns and make sketches. Students become more observant; they began to look for symmetry and patterns everywhere. The class creates a symmetry museum because students bring objects to school. They will have to explain how many lines of symmetry are on the object. Not all objects the students bring are symmetrical, so this starts a good discussion. We will investigate the use of symmetry on clothes. Students discover why clothes have lines of symmetry. Manipulatives will be used in a purposeful manner, not just for play.
Student Ownership
Throughout the unit, I want students to think independently and take responsibilities for their own learning. One strategy to do that is called Let Go and Let Students. This strategy allows students to showcase what they know how to do. Now students are expected to do work independently. After several guided practice activities, students will become the expert. They will create frieze patterns on their own. The patterns must represent any one of the seven examples of frieze pattern. Students will have to explain the type of pattern. The students demonstrate that they can draw lines of symmetry by creating a butterfly painting.
The next strategy that shows student ownership is Think-Pair-Share. This strategy requires students to think about a question and share their answer with a partner. The questions I ask are based on the math topic. For example, How many lines of symmetry does a square have? Or What happens when an object reflects over a line? Before students share out, wait time is given. Wait time encourages students to be actively involved in the question; and provides time to think. Students discuss answers with a partner. This allows students the chance to practice on one student before they share the answer with the whole class. Students hear their peers' ideas about math.
During this curriculum unit, students benefit from working in small groups or pairs. Students who need assistance can receive help from their peers. Sometimes students learn from explanations provided by their classmates. This opportunity gives students time to collaborate and work as a team. I use this time to observe students as they work on the assigned task. This lets me know who needs extra help with the topic. Students work together to act out the seven frieze patterns. A mathematician named John Conway generated frieze patterns in the form of footprint. Each pattern is represented by a motion or movement of the footprint. They are referred to as: hop, stem, jump, sidle, spinning hop, spinning sidle, and spinning jump. Students will show symmetry in motion. Using paint and butcher paper, students in pairs make the frieze pattern footprints. They will again explain what patterns they made. Students also use their feet to perform the various motions of the frieze pattern prints.
Classroom Activities
Before the unit starts, give each student a pre-assessment (See Appendix). After the assessment, I activate students' prior knowledge to find out what they already know about symmetry and geometry. The students complete a KWL chart. Then I read a picture book about symmetry to provide additional knowledge. There are several books you can read that I mention on the student bibliography page.
Lesson 1 (Parts: A, B, & C): Introduction to Symmetry
Objectives: Students will be able to find and identify lines of symmetry on objects.
Materials:
Cut-Out Objects (Shapes, Alphabets, Flags, Leaves)
Pencil
Overhead Projector
Math Journal
Vocabulary: Line of Symmetry
Part A: Distribute a cut-out heart to each student. Ask students to fold the heart in half vertically. Then draw a line on the folded line. Ask students, what do you notice about both sides? Are they the same? (Possible response: Both sides of the heart have exactly the same shape and the same size). Explain that when the halves on both sides of a line match in shape and size, we can say that figure is symmetric and we can call that line a line of symmetry. I define line of symmetry as a line drawn through a figure that creates two halves that are mirror images of each other. I give students cut-outs of other objects such as, a butterfly, square, triangle, circle, snowflake, and a person. I hold up each object and ask students if it has a line of symmetry. Based on student's answers, I fold each object to check for lines of symmetry. If an object does have a line of symmetry, explain to students that an object can possess more than one line of symmetry, such as the square or circle. Use the overhead to show students how to draw lines of symmetry. Now explain to students that not all objects will have line symmetry. Demonstrate this concept by giving each student a cut-out of a leaf/ another object (find one without line symmetry). Ask students to fold the leaf across the center. What do you see? Students notice that the leaf does not have a line of symmetry. The top and bottom parts of the leaf do not match. During this lesson the students can answer the following questions in groups.
What do you notice about the two sides of the object?
What is symmetry?
Does this object possess a line of symmetry?
How many lines of symmetry are there?
Part B
Symmetry in Alphabets
Objectives: Students will be able to identify the letters of the alphabet that have lines of symmetry.
Materials
1 bag of cut-out alphabets (3 students per bag)
Math Journals
Pencils
Give each group of students a bag of cut-out alphabets. Before students explore with the letters, review symmetry with the class. Allow students the opportunity to explain what symmetry means. Students can come to the board and provider an example.
After each group has the letters, students need to find the number of symmetrical letters. Students will put the letters in two piles: symmetrical and non symmetrical letters. Students record results in their math journal.
Challenge Activity
Students will find out the number of symmetrical letters in their first and last name.
Part C
Symmetry in Art
Objective: Students will create a butterfly with at least one line of symmetry.
Materials:
White Construction Paper
Liquid Paint (Different Colors)
Teaspoon
Give each student a piece of white construction paper folded in half. Have students open the paper and place two or three teaspoons of different colored liquid paint on their paper. The students need to close the paper and rub the top. Demonstrate first, showing students how to rub the paper carefully and thoroughly. Once students open their paper, they will see asymmetrical butterfly. Display the art work around the room.
Lesson 2: Symmetry Around Us!
Objective: Students will be able to identify symmetry found in nature and architecture. Students will observe and draw at least 5 different objects that have symmetry.
Materials:
Math Journal/Sketch Pad
Pencil
Camera
Photographs of Chicago Buildings
Book: Symmetry (My Path to Math)
Part A: This activity requires a field trip around the neighborhood/city looking for symmetry. During the walk, students observe and sketch objects, such as flowers, insects, and buildings. Some students are chosen to take pictures on the trip. Students include the line/lines of symmetry in their drawings. Students must label their drawings. I point out different buildings or architecture as we walk around the city. Questions are asked about the symmetry observed. I also give students important facts about the buildings. After the walk, students write a paragraph in their math journal about the trip. Students share their paragraph and drawings with the class. Once the pictures have been developed, students discuss the symmetry in the pictures. As the teacher, you must remind students that math is all around us; allow students to see the connection.
Part B: The teacher reads aloud Symmetry (My Path to Math). This story provides real world symmetry examples. On every page of this book, the author challenges students to complete symmetry related problems. For example, students must find and list all the symmetrical objects in their house or create a building that has a line of symmetry. After I read the book, students must complete one activity challenge and share with the class.
Lesson 1 and 2 provide students with a solid background of identifying line of symmetry. Students are aware that symmetry is found everywhere in nature and architecture. Lesson 3 focuses more on teaching students about the types of symmetries: reflections, rotations, translations, and glides.
Lesson 3: Frieze Patterns
Objectives: Students will be able to identify 5 out of the 7 frieze patterns. Students will be able to create their own frieze pattern designs.
Materials:
Pictures of the 7 Frieze Patterns
Math Journal
Pencil
Art Supplies (Markers, Crayons, or Paints)
Construction Paper
Frieze Pattern Templates
Overhead Projector
Vocabulary:
Frieze Pattern
Reflections & Glide Reflection
Rotations
Translation
Part A: I will show (Use Overhead & Pictures) and tell students about the frieze patterns. I will explain how frieze patterns are found on buildings, clothes, vases, and other objects. Students will get the opportunity to look at several examples of the pattern. Using the overhead, I will show students all 7 patterns, discussing them one at a time. I will model how the patterns have translations, reflections, rotations, and glides as symmetries. I define the symmetry vocabulary and write them on chart paper. Students record the same information in their journals. In groups, students identify the different types of frieze patterns.
Part B: I review symmetry vocabulary: reflection, rotations, translation, and glides by using frieze patterns from previous activity (Part A). Today students will apply Conway's' footprint movements to each frieze pattern. Pattern 1-Hop, Pattern 2-Jump, Pattern 3-Sidle, Pattern 4-Spinning Hop, Pattern 5-Spinnng Jump, Pattern 6-Step, and Pattern 7-Spinning Sidle. First I model how the movements look. As I move, students guess which pattern the movement represents. Then students will perform the movements.
Part C: Student Choice. In order to demonstrate an understanding of frieze patterns, the students can do one of the following: Option 1: Create five different frieze pattern designs using art supplies. Label each pattern. Option 2: Create five frieze footprint patterns using your feet, paint, and butcher paper. Label each pattern.
Notes
- Illinois State Board of Education
- Everyday Math Curriculum Resource Page (University of Chicago)
- National Council of Teachers of Mathematics (NCTM)
- Math Website: www.papajan.com/math/learn.html
- Christy Knuchel, Teaching Symmetry in the Elementary Curriculum, 2004
- Jill Britton, Symmetry and Tessellations, 2000
- Roger Howe, Continuous Symmetry
Bibliographies
Student Bibliography
Murphy, Stuart. Let's Fly a Kite. Harper Collins Publication, 2000.
This picture books presents symmetry in the form of kites. The illustrations definitely provide multiple opportunities to discuss symmetry. The author also gives ways of exploring symmetry.
Shaw, Charles. It Looked Like Spilt Milk. Harper, 1993.
This book encourages students to use their imagination to figure out spilt milk designs. Many of the spilt milk designs are symmetrical. The students have to wait until the end of the story to find out about the mystery designs. Teachers can use the designs as a symmetry lesson.
Peppas, Lynn. Symmetry (My Path to Math). Crabtree, 2009.
This book presents symmetry in a simple way. The pictures show real people and objects. Students view symmetry as it relates to the real world. The author challenges students to complete different symmetry tasks.
Websites: The following sites provide students with additional information about symmetry. Students are exposed to the symmetry vocabulary terms. They also get to view short symmetry clips. The teacher can also print symmetry sheets for extra practice.
Kids Can Have Fun. http://www.kidshavefun.com/math-activities.htm
Links Learning for Kids: Math Illustrated Lessons. http://www.linkslearning.org/kids
Teacher Bibliography
Barker, William; Howe, Roger. Continuous Symmetry. American Mathematical Society, 2000. This book thoroughly explains the fundamentals of symmetry. The illustrations vividly describe the concepts of each chapter. You also have the opportunity to take a close look at wallpaper and frieze patterns
Britton, Jill. Symmetry and Tessellations. Dale Seymour Publications, 2000.
This book provides teachers with background knowledge of symmetry and tessellations. Teachers are given activities to use in the classroom. The activities contain vocabulary and a step by step lesson plan. Additional templates or student practice sheets are also provided for each activity.
Libeskind, Shlomo. Euclidean and Transformational Geometry-A Deductive Inquiry. Jones and Bartlett Publishers, 2008. This book provides information about symmetry. Your math knowledge will be enhanced as you go through deductive inquiry.
Knuchel, Christy. Teaching Symmetry in the Elementary Curriculum. The Montana Mathematics Enthusiast Volume 1, No. 1, April 2004.
This article relates symmetry to the real world. The author explains why symmetry is important. Teachers are also provided with lessons to use in the classroom.
Appendix
State Goal
STATE GOAL 9: Use geometric methods to analyze, categorize and draw conclusions about points, lines, planes and space.
B. Identify, describe, classify and compare relationships using points, lines, planes and solids.
9.B.1a Identify and describe characteristics, similarities and differences of geometric shapes.
9.B.1c Identify lines of symmetry in simple figures and construct symmetrical figures using various concrete materials.
9.B.2 Compare geometric figures and determine their properties including parallel, perpendicular, similar, congruent and line symmetry.
(Illinois State Board of Education)
Sample Assessment (Pre/Post)

Comments (0)
THANK YOU — your feedback is very important to us! Give Feedback
