Introduction

I have only one short hour a day for math instruction and at third and fourth grade much of the time is used to teach algorithms and solving problems. Admittedly, I often prioritize teaching algorithms and steps so that children have the necessary skills to solve problems so that we can move forward onto new material. Teaching problem solving methods is satisfying. For example, when dealing with subtraction problems, training students to perform the standard right to left algorithm which involves (often blindly) crossing through a place value, reducing values by one, adding dashes to make values ten more and finally arriving at the correct answer feels like success! The success, however, is often disappointing when I ask a student to explain what he or she just did and explain why, he or she has only a shoulder shrug to offer, or a "that's just what you do to get it right" type of reply. The inclusion of place value concepts in the teaching of operations in elementary mathematics education may help students obtain not only a right answer, but also a reason for why the answer is correct. The intent of this unit is to tie the concepts of place value to operational algorithms in order to provide students with a conceptual understanding of addition, subtraction, and multiplication, and not just a procedure.

I teach in a third and fourth grade classroom at Westcott Elementary in Chicago, IL. The students are in my classroom for both third and fourth grade. Westcott consists of ninety-nine percent African-American students. Additionally, one hundred percent are classified as low-income families and qualify for free lunch. The school's population is transient due to housing and income based issues. These two factors also affect attendance and student performance. My students have a fragile concept about the composition of multidigit numbers, and place value concepts in relation to operations. Karen Fuson states, "The evidence indicates that U.S. children do not learn place-value concepts or multi-digit addition and subtraction adequately and even many children who calculate correctly show little understanding of the procedures they are using (1990)." ¹ Fuson's research confirms my students' lack of understanding, but the issue is more widespread than just my classroom.

Objectives

This unit is intended for teachers of third and fourth grade, and emphasizes the teaching of place value concepts and grade level skills in operations of addition, subtraction and multiplication. The unit will be presented in four parts. It can be taught in full or by section based on need. My goal for this unit is to strengthen students' understandings of place value concepts through the instruction of multidigit addition, subtraction and multiplication.

Background

Place Value

The place value system is decimal notation. This allows a digit (i.e. one of the numbers 0,1,2,3,4,5,6,7,8, or 9) to positionally indicate powers of ten involved in the "base ten" decomposition of a number determined by its location. To illustrate with a simple example, in this system the notation "123" represents the number "one hundred twenty three". In this system, a particular place value is ten times the value of the place to its right, but only one-tenth the value of that to its left. The system's beauty of compacting numbers allows for reasonable representations of extremely large numbers in a space that is workable, but leads to misconceptions of actual values in the representation. The close proximity of one place directly next to the place to its right suggests relative closeness in value when in actuality it is ten times the value. As an example, consider the digit 7 located in the "ones" place (the rightmost place). Moving this digit 7 one place value to the left into the "tens" place gives a number with value of 70, or 7 x10, or 7 tens, or ten times greater than 7. The next place to the left is the "hundreds" place, and moving the digit 7 there creates a number with a value 700, or 7 x 10 x10, or 70 x 10. 700 is ten 70s or is 100 times the original 7 in the ones place. That is, these numbers look similar, but are far from each other in value.

The values 700, 70, and 7 are examples of related values in the base ten system. The genius of this system creates confusion of the system. My students can name place values and show the value of a digit in a place, yet they lack the understanding of the relationship between the values after the tens place and struggle with how the representation of digits is a combination of values. Students are often confused by the values represented in the compacted form of the number. For example, if a student is asked what numbers are represented in 123 the response is often one, two and three. The correct response is 100 + 20 + 3. The error here is due to lack of a deeper understanding of place value. A student providing the correct answer indicates that they have deep understanding of place value and positional notation.

How can we overcome misunderstandings in place value? In Roger Howe and Susanna S. Epp's essay "Taking Place Value Seriously: Arithmetic, Estimation, and Algebra" ² the authors support explicit instruction of place value to students to create a more unified and conceptual understanding of the place value system with emphasis on the structure and systematic organization. The place value system is a complex one in an efficient condensed form. The idea to take the compressed number structure (i.e. 123) and intentionally unpack the content (i.e. one hundred plus twenty plus three) emphasizes the place value concepts. This expanded notation not only allows for an increase in conceptual understanding, but also allows for more computational flexibility due to deeper understanding. Students have computational flexibility when they can chose an algorithm or strategies that works best for the information presented. This unit will provide examples of different algorithms for addition, subtraction and multiplication.

Expanded form

The compacted number becomes more representative of value when shown unpacked in a variety of expanded form notation. If the number 7,892 is presented in compact form, its true value can be confusing for students. To clearly show students the parts of a compacted number, expanding the form shows each digit is connected to place value. For example 7,892 becomes 7,000 + 800 + 90 + 2. This form allows each number to be shown at its actual value. Now students can see the 8 in 7,892 as the 800 it represents. In another slightly more advanced expanded form, the number 7,892 is (7 x 1,000) + (8 x 100) + (9 x 10) + (2 x10). In this form, the digit is now the single place digit multiplied by the place value. In this form the place value is separated from the digit to show the number of 1,000s, 100s, and so on. The 8 again now shows 8 hundreds or 8 x 100. A third and even slightly more advanced expanded form additionally depicts increasing powers of ten. For example, 7,892 is 7 x (10 x 10 x 10) + 8 x (10 x 10) + 9 x (10) + 2 x (1). This form shows the single place digit, the place value and also how place value is constructed using powers of ten. Students see the 800 both as total value, single digit times the place value, and as a relationship between place values. The extraction of the single digit defines the digit and how it relates to positional place value. Expanded form explicitly shows digits to the left will always represent greater values than any earlier values because its place alone is worth more. The complexity of the number is better represented with expanded form notation.

Strategies

My strategies consider Epp's and Howe's advice to explicitly teach place value concepts, and integrate with this the teaching of the operations addition, subtraction, and multiplication. The unit will cover four strategies. In part one, "naming numbers differently," the objective is to emphasize place value in number names. This will aid students' place value understanding and help when expanding numbers into values. Part two, "addition of multidigit numbers," emphasizes importance of place value by using expanded forms of multidigit numbers when combining numbers. The addition strategies will use the expanded form to combine like place value terms. Part three, "subtraction of multidigit numbers," continues with expanded form and combining like terms but finding the difference in values. Finally, part four, "multiplication of single and multidigit numbers," builds upon the prior strategies and expanded form to continue the focus on place value in operations. The four strategies are introduced systematically to build on students' prior learning. Some of the introductory concepts may not require full coverage depending on students' prior knowledge.

Naming numbers differently and expanded form of compacted numbers ³

American culture falls into a category of cultures whose language characteristics do not lend well to understanding place value. Students write and say numbers that do not clearly show the value presented. As an example, the English word twelve tells us no information about its value of one ten and two ones. The compacted form of 12 does show the value positionally, but if positional notation is not well developed it may cause confusion. The example of fifty-seven gives more information because we hear fifty and seven, but the value of five tens and seven ones is not obvious, more can be done to show the places and values in 57. To enrich the learning of early place value, I will first spend time constructing a better understanding of the number names by teaching the conceptual place value and calling it "place value name" similar to the name given in Chinese based languages. Chinese based languages have a name for numbers that clearly represent the place value in the name. For example, twelve would be stated as "ten two," which corresponds to the positional 12 and the value of one ten and two ones. Also, fifty-seven in Chinese is stated as "five ten seven" representing the 5 tens and 7 ones related to the positional model of 57. This name will give students an understanding of real value not just the name for a number.

At the same time the instruction of "place value names" is being explained, students can begin to see the numbers as addition of place value components. For 12, the underlying ten plus two can be shown with a number model of expanded form of 10 + 2 or 1 x (10) + 2 x (1). The expanded form shows how the digits are positioned to create the numeral of 12. The value of 1 ten and 2 ones positionally is 12. The many names for numbers can be charted to show relationships across one number, 12. The expanded form is showing each digit times a value of ten, and the "place value name" always states the largest value first. The chart below is a tool to show the connection between numbers and place value concepts.

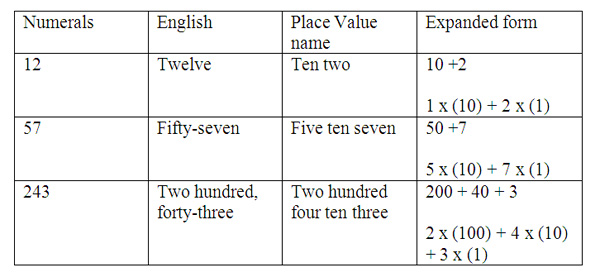
The naming of numbers many ways strengthens the understanding of their values, and also different ways to represent numbers. In later strategies students will use the knowledge of place value in singular numbers to perform operations.

Addition of multidigit numbers ⁴

Part one emphasizes the verbal importance of place value name as a tool to make place value parts noticeable in multidigit numbers. This strengthens overall positional understanding as it relates to place value, and simultaneously prepares students to transfer the knowledge of expanded notation to the operations of multidigit numbers. After students have practiced expanded notation of numbers, performing addition in a way that makes explicit use of the expanded notation is a natural step. Addition of multidigit numbers is traditionally taught by stacking the addends by place values in columns. We first add the values in the ones place, and then move left. If an exchange of ten is needed it is usually shown above the next column as a dash, one more. This process continues in an analogous way to the left across each increasing place. This method is efficient but does not teach the understanding of addition as a combination of values by each place. The following strategies for teaching addition are focused on both the operation and place value to give meaning to a procedural algorithm.

As described above, the expanded form of a number shows it as a sum of values corresponding to each place. The places are then put in sequence from largest to smallest value with an addition symbol between each place value (i.e. 123 = 100 + 20 + 3, or 1x100 + 2x10 + 3x1). Given an addition problem, rather than possibly blindly proceed through the 2-column algorithm just described, students can make use of the expanded form and combine "like" terms by adding the same place values together. As an example, if a problem asks students to solve 7,451 + 3,245 the strategy to place both numbers into expanded notation of (7x 1000) + (4 x100) + (5 x 10) + (1) and (3 x 1000) + (2 x 100) + (4 x 10) + (5) emphasizes place value position. It does not matter what place value the addition starts with because the sum will remain the same once all parts have been combined. The "any which way ⁵" rule from addition shows the sum is the same regardless of which place values are combined first. This strategy gives students more ways to solve the addition problem and deepens understanding about addition as a combination of values. The flexibility of adding any place value removes the restriction taught in column addition of always starting in the ones place. If the single digit is shown multiplied by the place value the addition can be simple by combining the single digits of the two addends (see the table below.) In this example, the thousands place shows 10 x 1,000 and this requires a trade of 10 thousands to 1 ten thousand.

For example, 7,451 + 3,245, traditional methods add from the ones place to the left. Traditional methods start with adding the ones (like the 2-column algorithm described above), but with the "any which way" rule, any place value can be added first. For example, if I chose to start in the thousands, or even the tens place, as long as all place value sums are combined to the total, it remains the same. Therefore, if students are taught a strategy that reflects the fact that "any which way" works to find the sum, they will have a better operational and place value understanding.

One can also perform multidigit addition in a similar way using any of the expanded forms mentioned previously. I plan to have the students work through different examples of expanded forms to add to flexibility.

Tools for teaching place value and multidigit addition

Teaching different strategies to solve multidigit addition problems can be supported with tools. Two tools that are useful are digit cards and number trains. Digit cards are index-card sized cards with the values 0,1,2,3…,9, and 10,20,30,…,90 written on them corresponding to the "ones" place and "tens" place respectively. Higher places (hundreds, thousands, and so on) are represented on cards similarly. A nice aspect to digit cards is that they can be used to show a number in expanded form and compacted form. The digit cards allow the student to see numbers as expanded form when each place is represented on the card and compacted form when placed down next to each other from largest value to smallest with each card slightly overlapping that to its left (obscuring zeros). Another tool that is useful is to make number trains to represent addition in a linear model. The train uses rods of different lengths to represent ones, tens and hundreds numbers to show addition. Both tools show representations of numbers in relationship to place value.

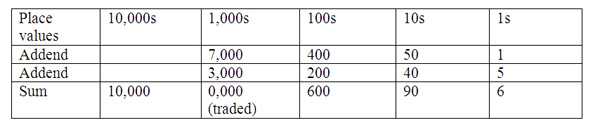
Digit cards can be used to show addition of multidigit numbers and allow for manipulation. To use digit cards as an example, 7451 is represented by the four digit cards 7000, 400, 50, and 1, which when laid next to each other left to right indicate expanded form. Digit cards can also be used to add multi-digit numbers. The problem of adding 7451 + 3245, for example, can be shown by combining place values in groups: the 7000 digit card is grouped with the 3000 digit card, the 400 digit card with the 200 digit card, the 50 digit card with the 40 digit card, and then the 1 digit card with the 5 digit card. The place value digit cards can be combined in any order, highlighting the fact that addition can be performed in any order. Once left with these pairs of cards, students can exchange the pairs for a single new card reflecting their sum. Here, students exchange for cards showing 6, 90, 600 and 10,000 (where in the last case, the sum 7,000 + 3,000 was exchanged for a higher place value card, 10,000). Placing the new cards down starting with the highest value will recreate the correct sum of 10,696 (see table below).

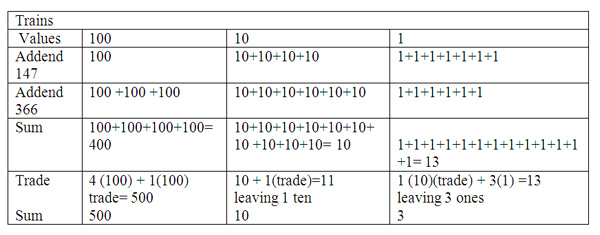
A different strategy to show addition using place value is a linear model that involves making number trains. This can be done using flat rods to represent 100, 10 and 1. I use a meter stick to represent a 100s rod, a "base ten long" as a 10s rod, and a "base ten cube" as a 1s rod. These last two objects are often found in classrooms. They are flat rods measured so that 10 "ten cubes" lined up left to right are the same length as a "base ten long", and 10 "base ten longs" are the same length as a 100s rod. Any objects with these same proportional relationships can be used. Roger Howe describes trains as lining up rods to represent addition of multidigit numbers. Trains allow children to see the sum value in the addition problem as two smaller values combining to make one greater value. The train starts with the first addend rods and adds the second addend rods. For example, given the addition problem of 147 + 366 one creates a number train by taking one hundred rod, four ten rods, and seven ones and creating a linear train. One then adds on three hundreds, six tens, and six ones. Next, combine like terms by reorganizing the train by placing all the hundreds together, all the tens and all the ones. This shows that the arrangement does not change the total sum while emphasizing the need to group like terms. Once the rods are grouped by place value, trade ten of any rods for one of the next greater value. For instance, trade ten ones for one ten, or ten tens for one hundred, as needed, and recreate the train with the regrouped model. The example below is not to scale but shows a representation of how the numbers can be organized in a train.

147 as a train

The next step is to show the train 366 added on, 3 hundred rods, 6 ten rods, and 6 one rods. Then rearrange both 147 and 366 to have all the hundred rods together, all the ten rods together and all the one rods together. So placing 1+ 3 hundreds rods, 4 + 6 tens rods, and 7 + 6 ones rods together. The next step is to regroup the rods with 10 or more. When this step is done I will have 4 hundred rods, 10 ten rods, and 13 one rods. I now must regroup and trade. The train then is reorganized with 7 + 6 ones which trades for 1 ten and leaves 3 ones. The 6 + 4 tens now have 1 more from the ones trade for a total of 11 tens. This 11 tens will trade for 1 hundred rod and leave 1 ten rod. The hundreds now have 1+ 3 plus the 1 traded for 4 total hundreds. The new train after regrouping has 5 hundreds, 1 ten and 3 ones. The train strategy can be shown in the written model below.

These strategies for adding multidigit numbers are ways to show addition by "grouping like terms", that is, decomposing numbers into their place value components and then adding together "like" place value components. These strategies all connect back to the traditional compact form used in the 2-column addition algorithm but unpack the place values in each number to support conceptual understanding of place value and combining values. The exchanging done in these expanded form problems is a foundational concept but one that continues to be reinforced in all the strategies.

Subtraction of multidigit numbers

Subtraction is the inverse relationship to addition. The act of decomposing (as described above in addition) in subtraction is more challenging for students specifically when borrowing or trading is needed. However, similar place value concepts and strategies can be used, and students can work though the same problems modeled in addition (using place value) above. These things show a connection between operations and will therefore hopefully be familiar to students.

Starting with a problem not requiring a trade will show the process of finding the difference of single digit numbers in the place value. Expanding the form of the compacted numbers in a subtraction problem is the first step to combining like values to see the numbers as individual places. . For example, 375 – 124 expands to 300 + 70 + 5 and 100 + 20 + 4 or (3) x 100 + (7) x 10 + (5) x 1 and (1) x 100 + (2) x 10 + (4) x 1. To show the subtraction, each single place can be subtracted and then multiplied by the appropriate place value, (3 – 1) x 100 + (7 – 2) x 10 + (5 – 4) x 1. After the subtraction is completed the remaining number is (2) x 100 + (5) x 10 + (1) x 1, which in compacted form is 251.

Subtraction that does not require borrowing or trading, like the example just given, is traditionally easy for students to perform using the standard 2-column subtraction algorithm. Once trading or borrowing is needed, errors tend to follow. As a model, the problem 513 - 366 requires trading. However, if students have already performed the related addition problem (366 + 147) using decomposition into place value numbers, an inverse relationship between addition and subtraction can be shown, and should lead to a clearer understanding. In the related addition problem (detailed in the previous section) two trades occurred, so it seems important to point out two trades will happen in the subtraction operation. The expanded form of 513 is 500 + 10 + 3 and of 366 is 300 + 60 + 6, or 5 x (100) + 1 x (10) + 3 x (1) and 3 x (100) + 6 x (10) + 6 x (1). Combining like values shows (5 - 3) x 100, (1 - 6) x 100, (3 - 6) x 1. Because we cannot subtract 6 ones from 3, this problem needs an exchange of 1 ten to 10 ones. This is similar to the addition problem at the stage where we had to trade ones for tens. Now the subtraction of 13 – 6 is possible and 7 ones remain. The next step is to move to the tens place, 0 tens subtract 70; realizing a trade is also need to solve. Next, move 1 hundred to the tens as 10 groups of 10 tens plus the zero tens makes 100 – 60 = 40. The hundreds place now has one less hundred and contains 400, solve 400 – 300 without a trade has 100 remaining. The subtracted values of 100, 40 and 7 are now compacted to show the difference in the two values is 147. It is beneficial to show this subtraction side by side with the related addition of 147 + 366 so the trading can be seen in both models.

Tools for teaching place value and multidigit subtraction

The tools for supporting subtraction strategies are number trains and number lines. The strategies can be shown using the same rod train model used in addition and the number line can be used to visually show subtraction. The trains are set up similarly to addition, the first number (the minuend) is laid down first, next the number being subtracted (the subtrahend) is placed below it. This creates a visual model of showing the space difference between the two trains as the difference between two numbers. The next example, number lines follows a similar model. A number line is a horizontal line marked with a "zero" and a "one", placed to the right of zero. With this, every other integer can be placed on the number line. For example, the number 2 is placed to the right of 1 at the same distance 1 is from 0. The number 3 is placed to the right of 2 at this same distance, and so on. The minuend is found first on the number line, then the subtrahend is located. The student uses the number line to find the difference in numbers with the support of the manipulative.

The train model for subtraction uses a linear model to represent the subtraction algorithm. Since subtraction with regrouping is a challenge, two digit numbers will work best in the model strategy. For example the problem 54 – 28, first create the minuend, 54, linearly and then place the subtrahend, 28, below. The missing value, or difference, is the space between the two numbers. For example, if the subtraction problem 54 – 28 is given, create a linear train of 5 tens and 4 cubes with base ten blocks or rods (as described previously), and a second consisting of 2 tens and 8 cubes, placed immediately below the first. This model shows subtraction as the difference in the two values. With this positioning, students will see that there are not enough ones available to subtract 8 from 4, and an exchange of one ten is needed in the train representing 54. After exchanging a ten for 10 ones, the "minuend" now has fourteen ones from which 8 are to be subtracted. This exchange should be recorded on the written model just as with addition when trading occurs. The next step is to find the difference between the remaining four tens and two tens, and to show the solution as 26 (see figures below).

Train representation of 54-28

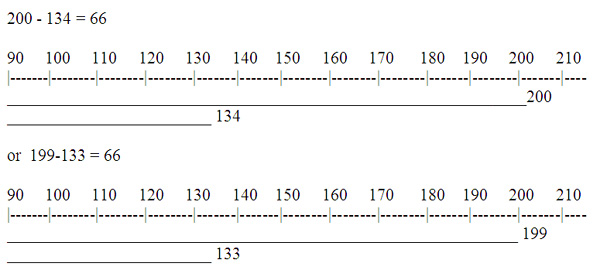
Another error prone subtraction problem involves "borrowing across zeros" to solve a problem. For instance, a problem like 200-134 is often the most challenging for students learning how to subtract with trading. The problem is due to multiple trades needed from the hundreds place to the ones place. Traditionally we would move to the hundreds place and redistribute the 1 hundred as 9 tens and 10 ones. A better strategy may be to use a number line or linear model to show 200-134. The number line is a useful tool for the subtraction algorithm and when "borrowing across zeros." Use a number line and find 200 and mark it, next find 134 and mark it. The number line can be used to see the difference between the two numbers as the space between the point marked 134 and the point marked 200. Subtracting with the number line can also sometimes be used to illustrate how to avoid trading or borrowing. The difference of the two numbers is traditionally found by subtracting the smaller number from the larger number to find the difference in the numbers. The difference between the numbers does not change if we move each number back one space on the number line, which corresponds to subtracting 1 from each. In this example, this translates to 200 – 134 = (200 - 1) – (134 - 1) = 199 – 133. Because we made the same change to both numbers the original difference 200 – 134 is still the same as the resulting difference 199 - 133. Compensating for both numbers by subtracting one from each does not change the difference, but it does make the subtraction easier because it does not require any trading or borrowing. Students can finish the problem by subtracting 3 ones from 9 ones, 3 tens from 9 tens, and 1 hundred from 1 hundred, for a total of 66. Some students may not be able to make the conceptual connection that shifting the numbers back one place on the number line does not change the difference between the values, but it shows how multiple zeros can be made into an easier problem. This strategy of compensation shows subtraction as difference and gives flexibility to solve problems.

Number line model

Multiplication of multidigit numbers

Multiplication of multidigit numbers is introduced in third grade and a standard in fourth grade. Multidigit multiplication is built on single digit multiplication knowledge. First, I will introduce strategies to students for single digit multiplication and build on the strategies and extend the strategies to multidigit multiplication.

Single digit multiplication

Multiplication of single digit numbers is the first introduction to the multiplication algorithm. Multiplication of whole numbers can be interpreted as repeated addition. The link to addition for student can be used in strategies to unpack the total value in a number model. I find it valuable to give multiple examples for each number model. For instance, the number 5 x 7 is the same as 5 sevens. Also, the strategies for multiplication of single digits can be shown with an array model. An array model arranges counters or items in rows and columns. For example, 5 rows of 7 counters, or 7 rows of 5 counters both make an array of 35 counters. The multiplication table itself can also represent an array of boxes or an area model. Students can use a multiplication table to cover with counters or shade over the numbers to show the area of 5 x 7 by shading 7 rows across and 5 columns for a total of 35 squares. This can be seen in the table below. Multiple strategies leads to flexibility and also deeper understanding of the multiplication concept.

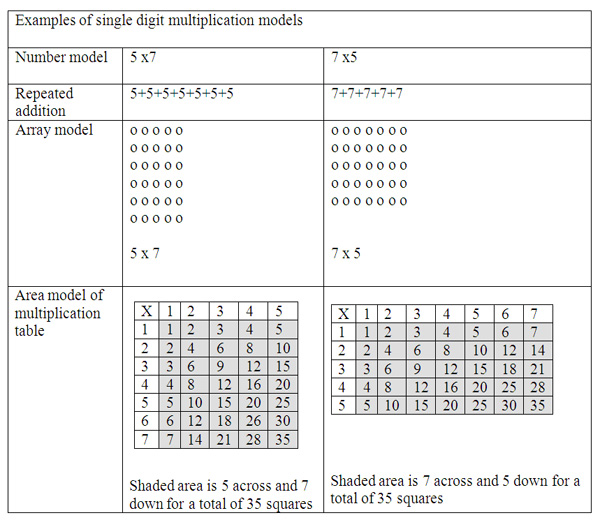
Multidigit multiplication extended single digit

I will introduce extended fact multiplication strategies after single fact multiplication models are understood. At first I will introduce strategies that can be taught as extensions of single digit multiplications. These types of problems will involve multiplication with "single place numbers" such as 10,20,30, and so on. For example, the extended fact problem of 5 x 70 should be connected back to the original single fact of 5 x 7. The connection should be made to the similarity and difference between 7 and 70. The digit is the same, but the place value is different. A model would be comparing 5 x 7 as five groups of 7 ones (for a total of 35) and 5 x 70 as five groups of 7 tens (for a total of 350). The link between the single digit multiplication and the extended fact is ten times the original fact. This can be illustrated multiple ways. For example, written in expanded form 5 x (7 x 1) can be compared to 5 x (7 x 10), where the difference between (7 x 1) and (7 x 10) is visible. One can also use the associative property of multiplication to rewrite 5 x (7 x 10) as (5 x 7) x 10, so that again the difference between this number and the single digit multiplication (5 x 7) is visible. This example allows a mental math advantage of seeing the original fact and multiplying by the place values presented. Students can recall most 1 through 9 facts, and can then apply this knowledge to extended fact problems along with place value concepts. By breaking the numbers into single digit values and place values the multiplication can be seen as two parts, the single digit multiplication and place value multiplication. The final step of multiplying the single digit by the place value makes the numbers easier to work with for the student because single digits are often known and multiples of ten are easy to work with for students. Another example, the extended form can also extend both original facts by 10, for 5 x 7 extended both facts to 50 x 70. The numbers are expanded to (5 x 10) x (7 x 10) and moving numbers through the commutative property to create easier combinations, of (5 x7) x (10 x 10). The original facts combine (5x7) and then the place value factors of 10 x10= 100 creating (5x7) = 35 and (10 x10) = 100, and then make 35 x100 = 3,500. The practice of finding the single digit multiplication and then the place value multiplication are manageable with mental math and support place value concepts.

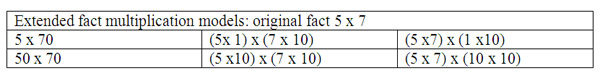
A connection here can be made to the addition "any which way rule." Multiplication has the same rule; order of multiplication does not change the product. For example, I can multiply 5 x 70 as (5 x 7) x 10 or (5 x 10) x 7, and any way I multiply will find the same product. The expanded form of the multiplication problem can be combined any which way works best for the problem solver. For example, I might use an example like 50 x 70, and first illustrate that this is equal to (50 x 10) x 7 = 500 x 7 = 3,500. I might then move the numbers to a new position of (5 x 7) x (10 x 10) to show that this same product equals 35 x 100 = 3,500. The expanded form of a number shows place value importance, while it applying single digit multiplication.

Multidigit multiplication

The next level of multiplication is a multidigit number that is not a single digit extension (like the examples above) such as 325 x 4. I will start with three digits by one digit multiplication. First, expand 325 to 300 + 20 + 5. All place value parts of 325, 300 + 20 + 5, are multiplied by 4. I then have to solve 300 x 4, 20 x 4 and 5 x 4, but the "any which way rule" allows me to chose the order in which I solve. I prefer to move from ones to hundreds and from hundreds to ones as it reinforces the any which way rule. I prefer to write the multiplications to be performed in a vertical table as follows:

The next step is to add the resulting products: 1,200 + 80 + 20 = 1,300

Another algorithm that is place value focused and also practical for computation is to consider each factor in a multiplication problem as a "team". An example problem is 37 x 21. Each factor 37 and 21 can be separated into place value parts, or teams of numbers (30 +7) x (20 +1). The next step is to multiply both expanded numbers with the other factor's members, that is to perform multiplication of each expanded value with the expanded value in the other factor. The strategy indicates 30 needs to multiply by 20 and 30 needs to multiply by 1 and that 7 needs to multiply with 20 and with 1 (see table below). Because this can be confusing I like to color code each number with colored pencils so as not to mix up which digits need to be multiplied. For example, I would color 30 + 7 red and color 20 +1 blue and state that you do not multiply numbers of the same color, and instead explain that each number of one color team has to be multiplied by both terms in the other color. This example shows the expanded form of both numbers and the multiplication of the single digits of each number, and then multiplying by place value.

The strategies explained in all sections of operational strategies are linked specifically with place value concepts and use expanded form repeatedly to build students' place value understanding in operations. This connection of operations and place value provides practice of algorithms while creating understanding of how the operations relate to place value and why place value understanding is crucial to deeper understanding of operations.

Activities

The activities will match each strategy section above for use in the classroom.

Activity 1: Naming numbers and expanded form

Materials:

Playing cards 1-9, four of each card

Place value mat

Score sheet

Students will practice building two digit numbers, naming the place value name, writing the expanded form, and determining the number with the greatest value. This activity is in a form of a game. The object of the game is to form the largest value with two playing cards. First, students draw two cards each. The student will decide which number to place in the tens and ones place. The student is trying to create the largest number from the two cards drawn. The student then places the cards on the mat, either in the tens place or the ones place, and record the information for his or her cards on the score sheet. The partner does the same task and the two students determine who has the larger value. The student with the larger value takes all four cards and wins the round. This game practices the naming of numbers and expanded form but the act of making the largest value practices place value concepts of understanding the tens place has more value, regardless of digit, than the ones place.

Sample Round

Student A draws cards 4 and 7. To make the largest value she places the 7 in the tens place and 4 in the ones place making the number 74. Student B draws cards 1 and 8. Student B places card 8 in the tens place and card 1 in the ones place making the number 81. The score sheet shows:

The game can add variations depending on class need or student need. One variation could include three digit numbers. Another, the game could be played with multiple players, the player with the largest number taking all the cards played in the round. To add to strategy the players could each draw three cards and then chose which two to play and have one to discard. The score sheet could include a base ten picture representation. An assessment for the activity beyond the score sheet is to have the student explain why placing the higher value in the tens place makes a more valuable number. Another ideas is to have a response sheet giving a scenario and having the student respond, "Carla draws a 1 card and a 9 card, which place should each card go to win the round? Explain to her why this creates the highest value?" Another way is to pose a mistake scenario, "Carla draws a 1 card and a 9 card, she places the 1 in the tens place and the 9 in the ones place, she loses the round to her opponent, what advice would you give Carla to have a winning strategy?" Both questions ask the student to use place value concepts and understanding in the reply.

Activity 2: Addition of multidigit numbers

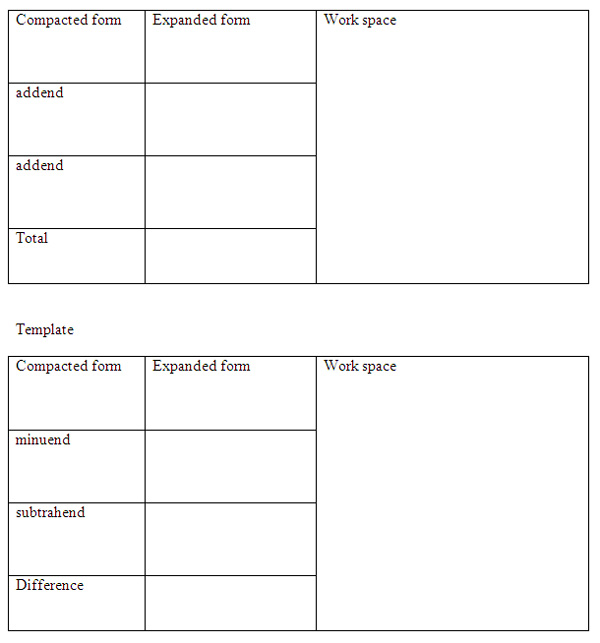
The addition of mulitdigit numbers is interesting when using relatable real world examples with students. Examples of attendance at professional sports games, heights of buildings or mountains, or distances on a map are examples of problems with meaningful context. For instance, my family is planning a trip from Chicago to Detroit and then Detroit to Cleveland. The distance to Detroit is 281 miles and the distance from Detroit to Cleveland is 169 miles. How many total miles will my family drive? The problems can be of any multidigit make-up and should have variety, some with and some without trade. The importance is not the values but the practice of expanding the form of each number and combining like terms. The table below shows the different expanded forms students can chose from the strategies. The student work should replicate the model shown for each step of the solution.

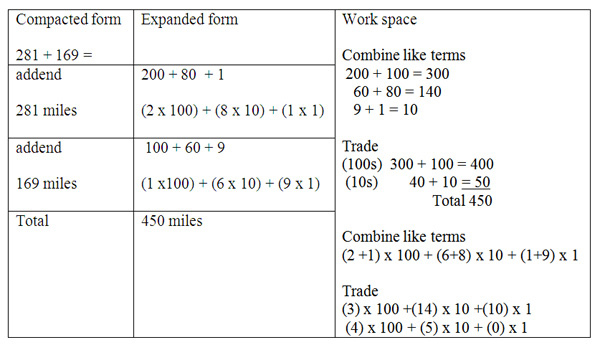
The students could also construct the addition problem with rods to make trains. The first train would have 2 hundreds rods, 8 tens rods and 1 ones rod. The second train added would have 1 hundreds rod, 6 tens rods and 9 ones rods. The reorganization of rods with like place values will have 3 hundreds rods, 14 ten rods and 10 ones rods. An exchange is needed in the ones place, exchange of 10 ones rod for 1 ten rods leaves 0 ones rods. Then exchange 10 of the 15 tens rods for 1 hundreds rod, leaving 5 tens rods, then counting the total 4 hundreds rods. The total train after exchange has 4 hundreds rods, 5 tens rods and 0 ones rods.

Activity 3: Subtraction of multidigit numbers

The use of real world examples and problems is excellent for subtraction problems. The link to real world in both addition and subtraction operations gives students practice at solving word problems and using examples of real math situations. An example question, The Willis Tower is Chicago is 442 m in height, the John Hancock Center in Chicago is 343 m in height. How much taller is the Willis Tower? The template for subtraction is similar to the addition template and allows for the same expanded number and combination of like terms.

Template

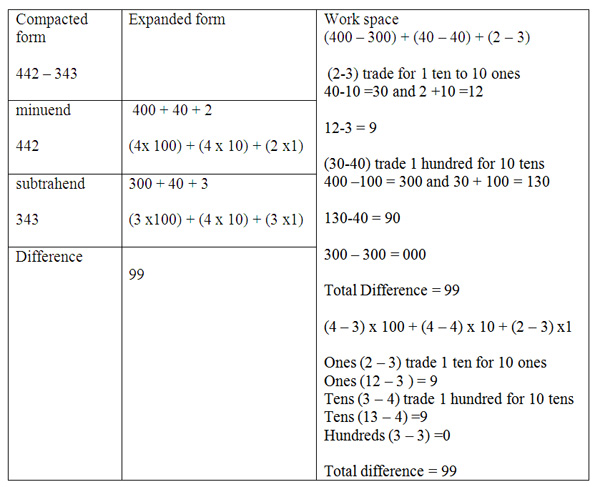
The train model can also be used to model the subtraction process. Make a minuend (total number and starting value) 442 train with 4 hundreds rods, 4 tens rods, and 2 ones rods. Next make a subtrahend (number subtracted) rod below the minuend with 343 train of 3 hundreds rods, 4 tens rods and 3 ones rods. The difference can be shown exchanging 1 tens rod for ten ones and then removing three from both trains, leaving 9 ones. The minuend now has 3 tens rods and 4 tens rods need to be subtracted so an exchange of 1 hundreds rod is needed. The hundreds rod exchanges for 10 tens making 13 tens subtract 4 tens leaving 9 tens. The hundreds rods are now equal at 3 which leaves 0 hundreds rods remaining.

Another way to solve is with the number line. On the number line find the Willis tower height of 442. Next, find the height of the John Hancock at 343. The student can count up to 343 to 350 and record 7 then skip count by 10s from 440 count 360 as 10 more, 370 as 20 more 380 as 30 more, 390 as 40 more 400 as 50 more until 440 is 90 more. At 440 counting to 442 is 2 more. The student can now combine all the counted up values of 7+90+2 for a total of 99 more.

Difference= 7+90 +2 = 99

Each word problem has a written model for the number model and then each step in the strategy can be shown in the workspace in each template. The written steps to solve are a way to track thinking for students and to express conceptual understanding. The step-by-step solving can be reduced to traditional methods once the student has strong conceptual understanding. The tedious process of unpacking each stage is time consuming in the beginning, but is meaningful and supports students' understanding of place value concepts.

Activity 3: Multiplication of multidigit numbers

The multidigit multiplication activity is fun for students to create their own problems from advertisements or sports pages of a newspaper. An example would be for a student to find an item for sale in a local advertisement. An electronics store may have computers on sale for $549. If the student wants to determine the cost for an entire classroom of 24 students to have a personal computer how much would all the computers cost? This problem provides real world examples and practices the skill of multiplication of multidigit numbers. The student could solve using the grid or by putting each with each by place value. For the grid the student could create a 3 x 2 grid and place the 500, 40 and 9 (from the expanded form of 549 as 500 + 40 + 9) along the top of the grid. Then place the 20 and 4 along the vertical side. Fill in each grid space with the product from the vertical and horizontal numbers on the grid. Add all the grid products to find the total. The other option is to solve with the "each with each" strategy of expanded both numbers and multiplying each factor place value by the second expanded number.

The students can find and create their own problems and then solve (as shown above) with each step in the process. Taking the steps to combine place values in the addition of the products reinforces the combination of like terms in place values and also the trading 10 to the next place value to exchange for one. In the problem above, 110 was broken into 100 +10 and then combined 1 hundred with the 900. Even as the most advanced problem in the activities the basic skills of exchanging and place value concepts are practice and reinforced in this type of problem.

An example of a sports problem could be a Chicago Bear running back ran for an average of 95 yards a game for 11 games. How many total yards did he run in the 11 games using his average yards per game? In this example, the student can use the same two strategies of the grid or the each with each strategy. If the grid is chosen the 90 and 5 can be placed horizontally and the 10 and 1 can be placed on the grid vertically. In the case of each with each 90 is multiplied by 10 and by 1 and the 5 is multiplied by the 10 and the 1, so each term is multiplied by the other factors terms.

Each of these activities uses examples that students can find in real life and the problems make math operations meaningful. The strategies to solve have students unpack the problems into place value expanded form and practice combining like terms and trading. The combination and trading are at the root concepts of place value understanding. The step-by-step problem solving allows the students' to articulate each part of the process in the operation and can support students when explaining how and why a solution to a problem is found.

Materials List

Base ten blocks – Base ten block manipulatives traditionally have ones cubes, ten cubes as one tens rod and one hundred cubes together on a square flat representing hundreds. These concrete objects allow children to move and manipulate number models.

Digit cards – Digit cards are representative of the place value numbers in expanded form. The digit cards have each place value with 1-9 digits on each card. The thousands place digit cards have 1,000, 2,000, 3,000, 4,000, 5,000, 6,000, 7,000, 8,000, and 9,000. The number 4,562 can be shown by taken the digit cards 4,000 and 500 and 60 and 2.

Number lines – Number lines can be traditional measurement style number lines or can be created to show skip counting of numbers depending on a student's needs.

Rods – Rods are place value representatives similar to base ten blocks but are linear models. The one cube and ten rod are similar to the base ten blocks but a hundreds rod is a long rod that shows the length of one hundred.

Activity Sheets – The activity sheets below are paired with activities 1 and 2 from the section above.

Activity 1: Game sheet

Activity 1: Score sheet

Activity 2: Addition of Multidigit numbers

Template

Works Cited

Carroll, William. Karen C. Fusion, and Jane V. Drueck. "Achievement Results for Second and Third Graders Using the Standards-Based Curriculum Everyday Mathematics." Journal for Research in Mathematics Education, May 2000.

Cross, Christopher T., Taniesha A. Woods, and Heidi A. Schweingruber. Mathematics learning in early childhood: paths toward excellence and equity. Washington, DC: National Academies Press, 2009.

Everyday Mathematics Grade 4. Chicago: Wright Group/McGraw-Hill, 2004.

Fuson, Karen C. "Issues in Place-Value and Multidigit Addition and Subtraction Learning and Teaching." Journal for Research in Mathematics Education

Ho, Connie Suk-Han , and Fanny Sim-Fong Cheng. "Training in Place-Value Concepts Improves Childrenâé™s Addition Skills." Contemporary Educational Psychology, October 1, 1997. http://www.sciencedirect.com/science/article/pii/S0361476X97909474 (accessed July 11, 2011).

Howe, Roger, and Susanna Epp. "Taking Place Value Seriously: Arithmetic, Estimation, and Algebra." http://www.maa.org/pmet/resources/PVHoweEpp-Nov2008.pdf. http://www.maa.org/pmet/resources/PVHoweEpp-Nov2008.pdf (accessed May 7, 2011).

Howe, Roger. "Developing and Interpreting Multiplication and Division with the

Number Line."

Howe, Roger. "The number line and addition and subtraction."

Ma, Liping. Knowing and teaching elementary mathematics teachers' understanding of fundamental mathematics in China and the United States. Mahwah, N.J.: Lawrence Erlbaum Associates, 1999.

Varelas, Maria, and Joe Becker. "Children's Developing Understanding of Place Value: Semiotic Aspects." Cognition And Instruction 15, no. 2 (1197): 265-286. http://www.jstor.org/stable/3233767 (accessed June 27, 2011).

Implementing District Standards

STATE Goal 6: Demonstrate and apply a knowledge and sense of numbers, including numeration and operations (addition, subtraction, multiplication, division), patterns, ratios and proportions.

B. Investigate, represent and solve problems using number facts, operations (addition, subtraction, multiplication, division) and their properties, algorithms and relationships.

6.B.2 Solve one- and two-step problems involving whole numbers, fractions and decimals using addition, subtraction, multiplication and division.

C. Compute and estimate using mental mathematics, paper-and-pencil methods, calculators and computers.

6.C.2a Select and perform computational procedures to solve problems with whole numbers, fractions and decimals.

6.C.2b Show evidence that computational results using whole numbers, fractions and decimals are correct and/or that estimates are reasonable.

Illinois state goals under goal six address number sense. Illinois state goals are arranged by grade band. For instance, the above mathematics standards are for "late elementary." The state of Illinois has five goals focused on number sense, estimation and measurement, algebra and analytical methods, geometry, and data analysis and probability.

Notes

1. Fuson, Karen C. "Issues in Place-Value and Multidigit Addition and Subtraction Learning and Teaching." Journal for Research in Mathematics Education
2. Howe, Roger, and Susanna Epp. "Taking Place Value Seriously: Arithmetic, Estimation, and Algebra." http://www.maa.org/pmet/resources/PVHoweEpp-Nov2008.pdf. http://www.maa.org/pmet/resources/PVHoweEpp-Nov2008.pdf (accessed May 7, 2011).
3. Ho, Connie Suk-Han, and Fanny Sim-Fong Cheng. "Training in Place-Value Concepts Improves Childrenâé™s Addition Skills." Contemporary Educational Psychology, October 1, 1997. http://www.sciencedirect.com/science/article/pii/S0361476X97909474 (accessed July 11, 2011).
4. Howe, Roger. "The number line and addition and subtractions." (Lecture)
5. Howe, Roger, and Susanna Epp. "Taking Place Value Seriously: Arithmetic, Estimation, and Algebra." http://www.maa.org/pmet/resources/PVHoweEpp-Nov2008.pdf. http://www.maa.org/pmet/resources/PVHoweEpp-Nov2008.pdf (accessed May 7, 2011).