- Login
- Home
- About the Initiative
-
Curricular Resources
- Topical Index of Curriculum Units
- View Topical Index of Curriculum Units
- Search Curricular Resources
- View Volumes of Curriculum Units from National Seminars
- Find Curriculum Units Written in Seminars Led by Yale Faculty
- Find Curriculum Units Written by Teachers in National Seminars
- Browse Curriculum Units Developed in Teachers Institutes
- On Common Ground
- Publications
- League of Institutes
- Video Programs
- Contact
Have a suggestion to improve this page?
To leave a general comment about our Web site, please click here
A Deeper Understanding of Fractions through Number Line Explorations
byJoe CondonLiping Ma
Introduction and Rationale
The way we teach the concept of fractions in much of the United States has been inadequate for too long. I have watched teachers representing the same fractions with the same pie diagrams for the past 20 years. Students have little concept of fractional values, struggle with algorithms involving fractions, find it difficult to prove equivalence and will generally do anything possible to avoid having to use fractions. I would like to address some of the mistakes I and other teachers have made in the past.
For years, I have asked students to order fractions and decimals on a number line. I've asked them this for multiple reasons: First, to assist in the understanding and practice of determining order and relative size of rational numbers. Second, to recognize that without being able to find common denominators for fractions, and an understanding of place value for decimals, it is very difficult to determine where some numbers should be placed on a number line. Third, to examine the distances between numbers on a line as a means for comparing values. In other words, the distance from 1/2 to 3/4 should not only be greater than the distance from 1/2 to 2/3, but have a proportional relationship so that the measurement of these distances can be used to place other fractions correctly on this length line. Theses three reasons have helped frame two of my objectives and goals for this unit. I believe the measurement and precision component of this unit will address many misconceptions regarding fractional value and offer an alternative way to look at operations (such as addition, subtraction, multiplication and division) with rational numbers.
If I give students a series of fractions to place on a number line, many of them will have the order absolutely correct. They will know through experience or use of common denominator calculations, factors and multiples of the numbers being worked with, that 1/2 is less than 3/4 and that 2/3 falls on a line somewhere between the first 2. Some may even divide the denominators into the numerators and get a decimal so they may use the strategies of "place value" to determine order. What most of the students are not able to do is place the fractions on a line with precision. A simplest example illustrating this is that students often do not depict the distance from 0 to 1/2 as the same as the distance from 1/2 to 1. Showing a measureable equality between the two distances may be achieved by some students, but I believe often only through sheer luck. I recently gave students in my 7 th grade Pre-Algebra courses a series of fractions and decimals to order on a number line of their own creation. I observed their process carefully and saw that students failed to use any tools to assist in the placement of non-"benchmark" fractions (i.e. fractions other than the familiar 1/2, 1/4, etc.). A few kids folded their paper in half to start the fraction/ decimal placements, but no student went beyond that. In fact, graph paper was made available to students and half of them chose not to use it. After reviewing their work it was apparent that the spacing/intervals were random.
The motivations for writing this unit came from a few different experiences I've had over the past couple years. In addition to what I've described above, I have witnessed year after year, students mistaking the measurement of an array by counting the lines instead of counting the space. This is significant because 2 dimensional geometry is actually taught as measurement, (a focus which number lines have not typically been afforded). The array in figure a. is a typical example of a 6 th and 7 th grade beginning geometry problem. Students will solve for perimeter in one of two ways: Some will
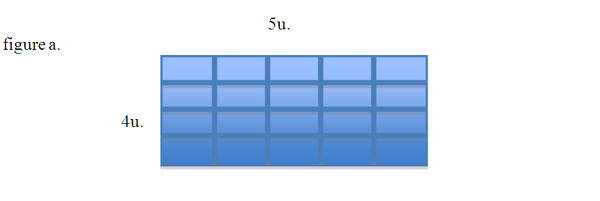
say that the length of the shape is 5 units and the width is 4 units. This gives us a perimeter of 18 units and an area of 20 square units. Others will argue that this is a 6 unit by 5 unit rectangle, giving us a perimeter of 22 units and an area of 30 square units.
On an even more basic level, given a number line (figure b.) of 7 units, fully 50% - 60% of 5 th and 6 th graders quizzed would claim the line to be 8 units long. It seems that whether we were working on a geometry unit or a simple number line , there was a significant percent of students not recognizing that units represent space instead of marks.

I teach in the Brisbane Elementary School District at Lipman Middle School. Over the past 3 years I have taught 6 th grade mathematics, 7 th grade pre-algebra and 8 th grade algebra. This was a difficult assignment over a three year period, not having a consistent curriculum to draw on and build upon made for busy curriculum design years. A benefit to this series of assignments was having the ability to see a middle school child's academic progression. The most positively striking progression I have noticed is their ability to understand and work in abstract concepts. The area of mathematics that seems to show the least amount of progression comes in the form of fractions. Whether it be determining value, simplifying, adding, subtracting, multiplying or dividing, most if not all students come with at best a lack of confidence and at worst a serious fear.
A lack of confidence when working with fractions combined with a lack of understanding that fractions have value is the basic premise I am working from in this unit. I believe that students will gain a clearer understanding of rational numbers, fractions in particular, when the concept is presented with context. Using a number line should go a long way in solidifying this understanding, so that the higher level mathematics our students are struggling will become easier.
In 1989 the National Council for the Teaching of Mathematics (NCTM) asserted that American students were woefully prepared for the rigors of secondary mathematics. Much of this stemmed from their superficial and algorithm based understanding of Proportional Reasoning. The study noted, "proportional reasoning is of such great importance that it merits whatever time and effort must be expended to assure its careful development." 1Students were taught methods such as cross products to solve for missing values in a set of ratios. They were not taught why they were doing this, nor it's applications beyond this one type of problem. In Liping Ma's book, Knowing and Teaching Mathematics, a teacher from China she was interviewing stated, "it is not enough to know how, we must know why". These words have been lost on many teachers of mathematics, many textbook companies, universitiies and of course on politicians, who in "pushing down" standards to lower grades in order to compete have effectively forced classrooms to teach on the surface of concepts instead of digging deeply into them.
Foundational Goals and Major Objectives
I will attempt to frame my objectives with both the 7 th Grade California State Content Standards and Common Core State Standards in mind. Briefly, both documents expect a student to extend their previous understanding of operations with fractions and analyze proportional relationships. To reach the three major objectives below, I have decided to take a few steps back to build a stronger foundation. I will first focus on two goals that will help address student misconceptions by presenting a method to look at the placement, order and value of whole numbers and fractions on a number line. I will also be looking at equivalence and basic operations in this alternative way. The Foundational Goals are as follows:
Foundational Goals
- Learn to use the number line to place, add and subtract whole numbers with measureable precision.
- Learn to multiply using a number line and gain a deeper understanding of this operation.
Major Objectives:
The Major objectives of this unit will be the focus of most background, strategies and lessons to follow.
- Students will understand what unit and general fractions are.
- Students will learn to compare fractions and determine equivalence while working with measureable, quantifiable precision on a number line.
- Students will learn to add, subtract and multiply fractions by using number lines and arrays.
While the major objectives represent the lion's share of my unit, many other content areas that will come up. Concepts such as place value, scaling, measurement, factors, multiples and 2 dimensional geometry to name just a few. The spiraling nature of a deeper curriculum is something to be embraced. Very little math happens in a vacuum, so we must acknowledge and encourage children to explore and question connections and tangents. We must take the time necessary to solidify long term connections. As we take a step backwards, we open up the possibility to cement so much more that seems to only hold a superficial place in the children's understanding of mathematics.
Foundational Goals Background
Number Lines
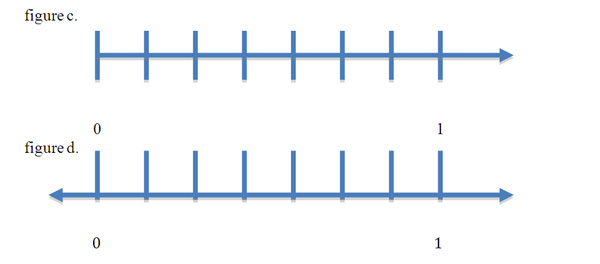
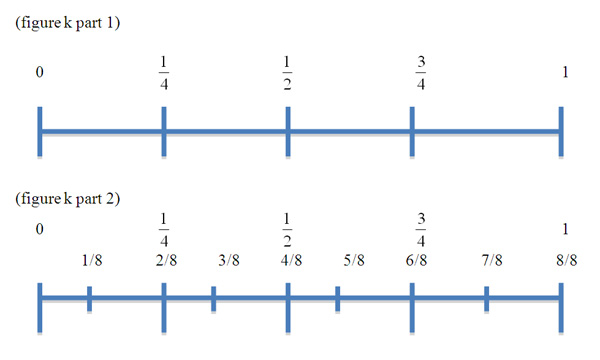
Number lines and rays are typically represented as horizontal lines. Positive numbers are equally spaced to the right of the zero and negative numbers equally spaced to the left. This concept of equality with regard to the iterations on a number line is clearly shown when placing whole numbers on a line. An equal measureable distance between each whole number will continue infinitely. A number ray is determined by a fixed point, (0 in figure c.) and continuing on infinitely in this one direction. A number line is determined by two points, a "zero" point and a "one" as shown in figure d and continues in both directions infinitely. For the sake of this unit our number lines and rays will only work in a positive direction or to the right of the "zero".
According to H. Wu of U.C. Berkeley,"as a model for fractions, the number line differs from other models in several important ways, first a length represents the unit, and the number line model suggests not only iteration of the unit, but also simultaneous subdivisions of all iterated units. That is, the number line can be treated as a ruler." 2 Each of these iterated units, when representing fractions will be 1/d, where d represents the number of units necessary to make a whole unit. In other words, when subdividing a line into ?, it will take 5 iterations to complete the whole (figure e.). These fraction concepts are explained in greater detail in the fractions section of my background.

Early number lines were most likely measurements also. Ancient Egyptians did not have a concept of zero, but are believed to have used lines with consistent intervals in order to gauge distance while building. The number line was founded with the idea of measurement, not counting. According to reports from the International Study Group on Ethnomathematics, "archeologists reference, 'leveling lines' that predate the pyramids. Lines that measure foundation depth and height using the ground as the zero level, or as the Egyptologist, George Reisner calls it, "Zero Lines". These zero lines were labeled nfr, or zero." 3 Level lines were evenly spaced above and below the nfr and labeled, 1 cubit above nfr, 2 cubits above nfr or 1 cubit below nfr, 2 cubits below nfr. Number lines have historically been tools for measurement. In this unit we will attempt to get back to this idea.
The basic operations of addition, subtraction and multiplication as well as measurement and division will be addressed in the strategy section for Foundational Goals.
Major Objective Background
Fractions
For the sake of this unit, the fraction background will be limited to: Unit fractions, general fractions, the equivalence of fractions, adding and subtracting fractions with like and unlike denominators and multiplication of fractions.
Unit Fraction
A unit fraction is a fraction of the form 1/d (for any positive integer d). The concept of the unit fraction 1/d may be the most important foundational step in the study of fractions. Students need to understand that 1/d represents one of d equal parts, with emphasis placed on the word equal. 1 of d equal parts can be illustrated on the number line by dividing the interval between 0 and 1 into d equal parts. The first segment represents the unit fraction 1/d, while the first two parts together represent 2/d parts. Each of the two parts being equal. The first 3 parts represent 3/d, (three of d equal parts) and so on. Susan Lamon acknowledges in her book, Teaching Fractions and Ratios for Understanding, that the ancient Egyptians used unit fractions extensively. These fractions whose numerators are all 1 are easy to compare. She points out that any unit fraction can be written as the sum of other unit fractions.

General Fractions
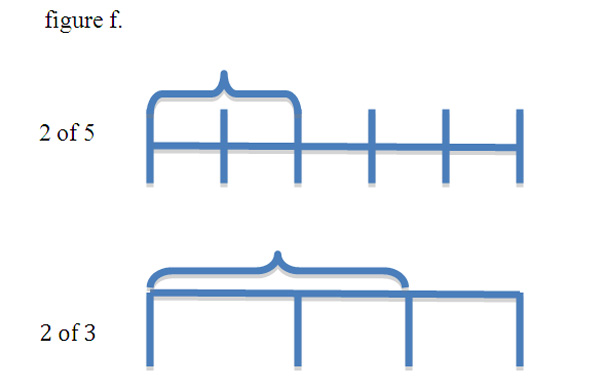
A general fraction is a non-negative rational number symbolically represented as n/d. Here, d is the number of equal parts of necessary to make a whole, and n is the number of copies of these equal parts. In other words, n copies of the unit fraction 1/d or (n)*1/d=n/d. The top number of a fraction is called the numerator and the bottom number is called the denominator. The denominator tells us the size of the pieces. The larger the denominator the smaller the size of each part since the whole is divided up into more parts. For example, 2/3 and 2/5 have the same number of parts, but2/5 has smaller pieces, (figure f.).
According to Lamon, "The order of the numbers is important. Thus, fractions are ordered pairs of numbers: 3/4 is not the same as the fracion 4/3" 4
Equivalence
"The Theorem of Equivalence may be regarded as the fundamental fact in the subject of fractions. Conceptually, its message is clear: the essence of the fraction symbol m/n lies not so much in the individual numbers m and n of the symbol but in their 'relative size' because m/n = 2m/2n=3m/3n ," 5 says Wu. This theorem helps us understand something we believe to be second nature to our children, that is, the idea that 1/2=2/4 is translatable to all equivalent fractions. Problems with this assumption arise when students are asked to compare fractions like 8/12 and 18/27. The relationship between these two equivalent fractions is not as easy to see as with 1/2=2/4, one which is a simple integer multiple of the other. Instead, the equivalence between 8/12 and 18/27 is most easily seen after reducing each to their simplified form of 2/3.
Addition and Subtraction of Fractions with Like Denominators
Our students have most likely already learned to add and subtract like and related fractions. Just in case these concepts are unfamiliar here is a quick review. Like fractions are fractions with the same denominator. Addition and subtraction problems involving like fractions involve only addition and subtraction of the fractions' numerators. Symbolically this would be represented as a/b+c/b=(a+c)/b. The denominators of these fractions are not summed because they represent the "whole".
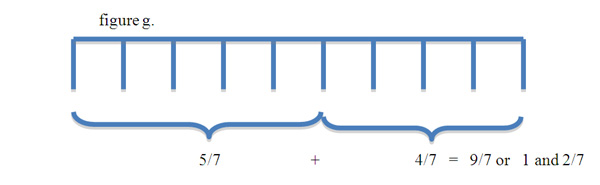
In some cases the sum of the numerators added will exceed the denominator value. This is when we begin dealing with improper fractions or mixed numbers. The addition problem 5/7+4/7=9/7, for example, is easily depicted using the number line. In this problem we have two fractions with the same denominators (7), so we will need only2/7 added to 5/7to complete the whole. We have 2/7 more than that giving us 9/7. Another way of reading this is, 7/7 makes one whole with 2/7 left over, giving us the mixed number of 1(2/7). An improper fraction is defined as a general fraction n/d where the number of parts (n) is greater than the whole (d). A mixed number represents the quotient of that improper fraction, thus 9 divided by 7 gives us 1 and 2/7.
Addition and Subtraction of Related Fractions
Primary mathematics standards describe related fractions as follows: "Related fractions are fractions where the where the denominator of one fraction is a simple multiple of the denominator of the other fraction." 6 Addition and subtraction problems involving related fractions require finding an equivalent fraction for only one of the set of two you are working with. The rules of equivalence will help the students at this juncture. To illustrate this concept, consider the addition problem 2/3+4/9. We can see that 3 is a factor of 9 so the only fraction that needs to be changed would be 2/3. If we multiply this fraction by 1, represented as 3/3, our new problem becomes: 6/9+4/9. Now we can sum these fractions as in the case of like fractions discussed above.
Addition and Subtraction of Fractions with Unlike Denominators
Adding and subtracting fractions with unlike denominators where the denominators are not simple multiples of each other is the step our students seem have most trouble with. If this is taken in a step by step process, where different grade levels have different responsibilities, I believe we would have much more success. The first step in dealing with unlike denominators would be to multiply the numerator and denominator of each fraction by the denominator of the other to obtain equivalent fractions that share the same denominator with each other. For example:

The second step would be to work with students to find the lowest common denominator of two unrelated fractions, alternatively called, the lowest common multiple, (lcm). This is a necessary step for students so they can work towards less simplifying after solving. Students should begin this step by learning to compare simple general fractions through experimentation with bars and number lines. Adding fractions like 2/3 and 3/4 will break down with bars and number lines in the same way. See figure
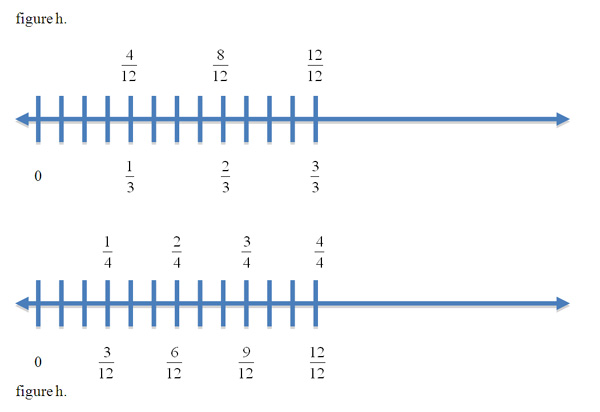
If students place iterations of each relevant unit fraction on a line, i.e. 1/3,2/3,3/3 and 1/4,2/4,3/4 and 4/4 then subdivide these lines into an equal number of total parts (d) or 12 for the sake of this example, they will be able to add, subtract and compare all iterations of the original fractions because these two general fractions now share a common "whole" or a common denominator. The denominator of 12 is found by recognizing the lowest common multiple (lcm) of 3 and 4 is 12.
I believe this next step in the process underscores my appendix advocating for revisiting common algorithms in higher grades. If we continue to open our students up to new ways of looking at basic concepts we will only strengthen their foundations.
Multiplication of Unit Fractions and General Fractions by Whole Numbers
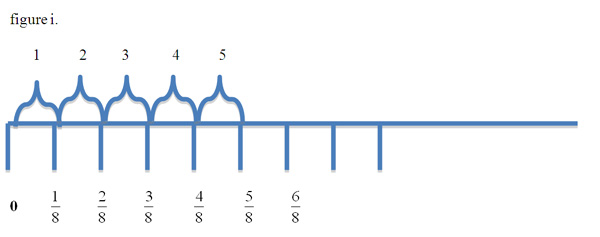
The initial multiplication operations fit neatly on the number line format. Multiplying a unit fraction by a whole number can be thought of as repeated addition of that unit fraction. A problem such as, (1/8) x 5, can be thought of as 5 iterations of the unit fraction 1/8. (figure i.).
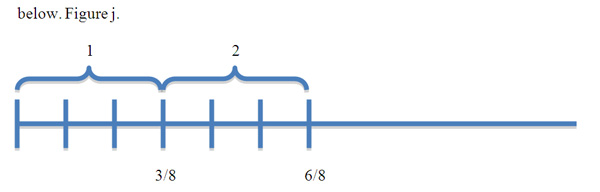
Multiplying general fractions by whole numbers such as, (3/8) x 2, will operate in the same way as iterating unit fractions. The difference being, we iterate every third unit (based on a 3/8 example), giving us a total of 6/8. This is illustrated with the number line
below. Figure j.
Multiplying Fractions by Fractions
Multiplying a fraction by another fraction may be best accomplished with a grid (array). It is also possible to multiply fractions by using the number line. I believe it is important conceptually to help students understand that the product obtained after multiplying two fractions will be smaller than either of the two original fractions. This situation is opposite from that of multiplication of two whole numbers: 15 = 5 x 3 is larger than both 5 and 3, while 1/15 = 1/5 x 1/3 is smaller than both 1/5 and 1/3. Using related unit fractions (whose denominators are factors of each other and whose numerators are 1) will be a nice entry into the concept. To illustrate1/2 x 1/4, for example, students could begin by finding the product of the relevant unit fractions 1/2 and 1/4 by subdividing a unit interval into fourths and then finding 1/2 of one fourth to obtain the product of 1/8. To find the original product of 1/2 x 3/4, students could proceed by continuing to subdivide each of the four fourths in half, and then iterating 3 copies of the 1/8 just found. The example below illustrates this concept.
It is important for students to have a concrete understanding of the product of a fraction before simply multiplying numerators and denominators. I believe having the students measure and plot these simple related fraction problems on a number line will go a long way towards the concrete understanding we are looking for.
Teaching Strategies
This unit should take approximately 3-4 weeks to teach. In this section I will go over ideas for daily activities and a general outline of the major concepts and how they break down. I want to encourage all teachers to strive for depth at each stage of the unit. Do not be afraid to delve into an aspect of the unit for a greater time than prescribed. This unit should be contextualized as much and as often as possible. I have used the number line throughout this unit to attempt to give the study of fractions a context in linear measurement. I have done this because I believe our students see fractions as division problems or part to whole relationships and not as rational numbers with value.
Number Talks
Throughout the year, I give number talks at least 3 days per week. A number talk is a 5 to 10 minute mental math problem that highlights the different ways our children solve problems. I will typically use these talks to reinforce foundational concepts such as addition, subtraction, multiplication and division. A problem like 327 + 468, can elicit some valuable information for the children and for that matter, for yourself. Students will solve these problems in multiple ways: some may simplify the numbers: 325 + 475 = 800 then subtract 7 and add 2 giving you 795. Some students may deconstruct the numbers: 400 + 300 + 20 + 70 + 7 + 8. Other students will gravitate towards what they feel comfortable with and stack the numbers and attempt to add in their heads.We need to understand how our children are approaching these "basic operations". Many students cannot escape traditional operations for addition, subtraction, multiplication or division. Seeing others break down numbers, use simple numbers or playing with place value will help many of those students feel more secure when experimenting with numbers.
I have found number talks to be most effective when working with basic operations. Number talks work well when we take the time to ask questions like: How did you think about that? Can you explain the process you used? How did you figure it out? Did anyone get a different answer? Giving children a chance to share their methods can be a powerful motivator for many students. Opening children's eyes to new methods of solving basic operations that they have not considered yet can be a game changer. Kathy Richardson's book, Number Talks, is a wonderful resource for this great daily ritual.
Addition, Subtraction, Multiplication and Division of Whole Numbers
Placing Cuisenaire rods and cubes end to end as a representation of addition and length can be very effective. I realize this will be a very simple section of the unit for our 5 th, 6 th and 7 th graders, but if we take the time to develop the process of concatenation of lengths, the connections when working with addition and multiplication of fractions will go along way in assisting with student understanding. Lesson #1 below, is an example of a possible direction one could take when opening up this unit.
Subtraction is a comparison of the difference of 2 rods. Laying rods next to each other, the greater rod on top, will give a visual reminder of subtractions as difference. Subtraction practice with rods, cubes and number lines should follow or be combined with the addition and placement lessons (lesson #1). Re-establishing the inverse connection between addition and subtraction is a strong step in building the foundations we are attempting to work on at the beginning of this unit.
Multiplication is a process of repetitive addition. If students practice concatenating lengths of the same unit, (i.e. 3 unit Cuisenaire rods) for a given number of times (i.e. 5) they will have a hands on model of the problem 3x5 and the operation of multiplication itself. This is modeled with rods and using a number line below.
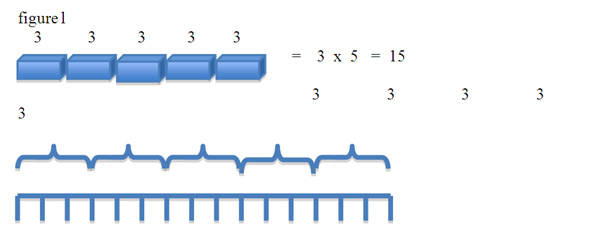
Division would work with rods and cubes as the reverse of multiplication. In other words, represent your dividend with, for example 3 ten rods and then find the different rods that will evenly divide this length. A nice lesson in factors and divisibility can come from this. As a student tries out lengths to fit evenly along the 32 unit row, they will be solidifying their knowledge of factors and the concept of division as the partitioning of a number into equal parts.
Re-introducing the number line and the number ray using whole number integers. Work on all four basic operations with whole numbers using the number line. Distance or linear measurement should be stressed. For each of the operations, students have had hands on experience using the rods and cubes, so they should move into this activity nicely. Students can also practice scaling up and down through multiplication and
division on whole numbers. This work should always be done with measurement in mind. For example, if we ask the students to draw a line 8 inches long and we split it into 8 equal pieces, then each piece would need to be 1 inch long. Every 4 pieces would be 4 inches long, etc… If we scale this 8 inch line up by a factor of 3, there will be 24 places on the line and 4 units on the line will be 12 inches long. Linear scaling is a fun and simple lead in to 2 dimensional and 3 dimensional scaling.
Fractions
We can compare, add, subtract, multiply and divide fractions using rods and cubes. Cuisenaire makes rods (discussed in the previous section) with a lengths of 2, 3, 4, etc… up to 10. Experimenting with these operations and having students coming up with the best procedures to solve may be a beneficial experience. I would open up each subsection of the fraction section of this unit with a period (or more if it is productive and beneficial) of rods and cubes. Then I will move into number lines for that particular subsection. In other words, compare fractional values with rods and cubes one day, then compare similar values on a number line the next. Working with arrays when you get to multiplication and division of a fraction by another fraction should be the only departure from this model.
Addition and Subtraction of Fractions with Like Denominators
As we Introduce fractions on the number line will we will need to take time to develop the concept of 1/d (as explained in the background section of this unit). This process can be represented on the number line very effectively. Let's suppose students are to add the like fractions 3/4 and 7/4. To illustrate this using the number line, a starting point would be to begin with the unit fraction Take for example, the unit fraction 1/4, four iterations of which give us the whole. We can continue counting equivalent fractions that represent

wholes by moving along the number line four units at a time until 2 wholes are reached at 8/4, 3 wholes are reached at 12/4, continuing infinitely. To answer the original problem of adding 3/4 and 7/4, students need now only to move from 3/4 seven units to the right to arrive at 10/4.
This is an interesting step for students to experiment with iterations of a unit or general fraction (addition). For example, I might ask the students, "what is 3/4 more than 1/4?" This process of moving a segment of the number line will reinforce length and give a clearer picture of addition. Allow the students to develop number lines that are d parts long, and fill in the iterations until they have 1 whole. Bringing measurement into this process will serve to reinforce concepts of value.
Addition and Subtraction of fractions using the number line follows the placement description above and the background section on equivalence. Given any two fractions with the same denominator, we are just combining the unit parts for addition and comparing the difference in unit parts for subtraction. Students practicing the subdivision of a line, through measurement, in order to add fractions with like denominators will be well prepared for the subdivisions necessary to find common denominators or lowest common multiples.
Addition and Subtraction of Fractions with Unlike Denominators
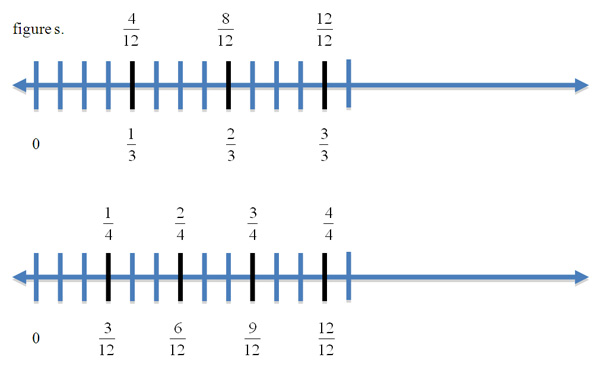
If given two fractions with different denominators, we will first follow the theorem of equivalence to create like denominators. This process described in the equivalence background section and the background section on adding and subtracting with unlike denominators begins with the basic algebraic principle of multiplying each fraction being added by the denominator of the other fraction. The product created will give you a common denominator to work with. Working with number lines and unlike denominators will be simple when the fractions are related or are obvious factors of the same number. Students will learn to divide a number line into d parts (thirds (in blue) for example) then subdivide each third into fourths (in black), creating a common denominator of twelfths (figure h) from which to work. Now if a student needs to add 1/3 + 1/4 they can find 1/3 as 4/12 on the line and add 1/4 equivalent fraction 3/12 to it, giving you 7/12. Students will know how to subdivide the number line when they use the theorem of equivalence and multiply each fraction by the others denominator. The initial subdivisions can be in thirds or fourths.
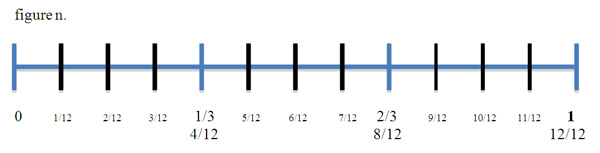
It will be a little more complicated when working with denominators that ask students to subdivide a line into 21 evenly spaced parts because the denominators being summed are 3 and 7. At this juncture it is important to ask ourselves, "does the model help in our students understanding, or am I just using it to stay consistent?" If we ground ourselves in the principle of "example sufficiency" 7 during the work with related and simple fractions, we should not need to burden ourselves with a model that may over complicate an idea already embedded.
Finally, students are ready for multiplication of fractions. Using the number line for related fractions, as shown in the multiplication of fractions by fractions background section, and arrays for related and general fractions that do not subdivide so easily, will serve the children well in giving them hands on, contextualized examples of fractions as numbers having value and taking up space.
Lesson #1
Objective: Students will be able to add whole numbers using rods, cubes and number lines.
Timing: 1 - 50 minute period
Materials: Cuisenaire rods and cubes, graph paper, rulers.
Opening:
Using an overhead projector or board in the front of the room, display the following number line.
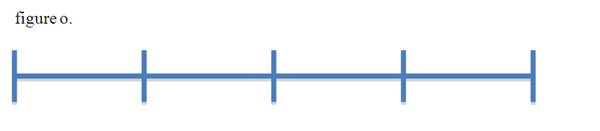
Ask the students to discuss with their group mates, how long this line is? Place answers from the class on the board/screen. (Possible answers: 5, 4, 1, etc…) Have students prove their answers. Offer them graph paper, rulers, calculators, anything they need to prove their hypothesis.
Go over these proofs with the class. We want students to justify their answers with the idea that these are all equal parts, so whatever unit they are counting by (d), the total length would be the iterations (n) times the unit 1/d. In other words, 1x4 or (1/4) x4 or
Symbolically (n)1/d. Discuss with the students how this breaks down. Gives lots of examples. It would be prudent to keep this in the positive integer, whole number realm for this opening lesson.
This opening will help students ground themselves in a unit to work with, that the iterations of this unit are the same and that each unit has value, (shown through length on a number line).
Student Experimentation/Documentation:
Using rods, cubes and the number line students will practice showing addition problems and then use those models to sum. This practice will be a way to help stop the tendency our students have of counting marks on a line or a grid. Moving them towards seeing number lines and grids as forms of linear measurement is our goal.
For each of the activities involving number lines, we will begin with the physical manipulation of rods and cubes. Students will need to begin by measuring the length of a rod with cubes in order to establish the concept of length in their own minds. Using Cuisenaire rods students will then create trains, end to end, to represent addition. After establishing this process with rods alone students should add cubes to begin working with 2 digit numbers that are not strictly powers of ten. See figure below.

These rods will translate easily to working on a number line. Given a problem such as 13 + 11, students should first attempt to draw this on a number line by bracketing 13 and 11 and finding the sum. It will be necessary to stop students that are not representing unit

values with the same amount of space. In other words, have them get out the ruler or use graph paper so the idea of the iteration of a unit, whatever it is, is represented by the same amount of space.
Once this is established moving into representing addition problems in expanded form will help students in many ways. The number line in figure d. shows the problem 13 + 11 expanded into 10 + 3 + 10 +1. This is a process we will continue with throughout this unit. For this lesson continue to have the students expand ever larger numbers. To differentiate, have students work with multiplication and/or powers of 10 when representing a deconstructed number.
Students should document their work with both the rods and cubes as well as number lines in either a math journal or on a separate sheet of paper. This will allow teachers a good anecdotal assessment opportunity. Be on the look out for students representing the same unit with different lengths.
Lesson #2
Objective: Students will learn to add and subtract fractions using a number line.
Timing: 2-3 – 50 minute periods
Materials: Rulers, graph paper, pre – made number lines (optional)
Opening: Write 1/3+3/4 on the board or the overhead. Have students discuss in their groups different ways to solve this problem. Groups should attempt to come up with at least 2 different ways. (algorithm, array(s), number line, manipulatives, drawings, etc…) Make note of the methods used. Keep chart if possible. Have groups share out in front of the class.
Student Experimentation/Documentation:
Give each table group rods and cubes and ask them to represent the problem with the manipulatives. Teacher should do the same on the overhead. Discuss what the problems with this representation might be. (Unlike denominators). Discuss the idea of like terms and why adding these two fractions is difficult without common denominators. (Be open to the possibility that a student will show how to do this without finding a common denominator. Using an array will allow a student to shade 1/3 of a rectangle horizontally and 3/4 of a rectangle vertically. If they count all the shaded area (count 2 for each overlapping grid piece) they will have solved the problem. The interesting part of this problem is when the students discover that they did actually find a common denominator, (12 grid pieces when dividing a rectangle into thirds horizontally, then into fourths vertically)).
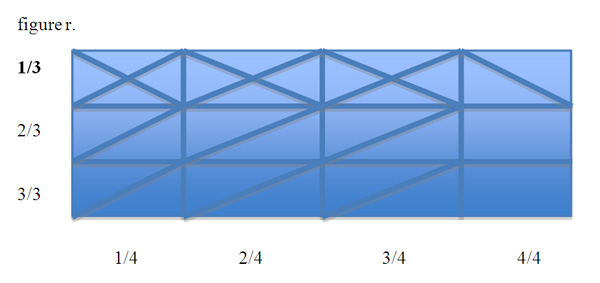
1/3 is denoted by diagonal lines going from the upper left to lower right of each cell in the top row. 3/4 is denoted with diagonal lines going from the lower left to the upper right in the first 3 columns of the array. If I add the number of cells that have "fill" I get the answer 13/12.
Now have the students work with you when transitioning to number lines. If they divide a line into thirds (black lines below), then subdivide each third into fourths (blue lines between each third), they will have created twelfths and can add the two fractions together. It will be important initially to draw a second number line representing fourths (black) and then subdivide each fourth into thirds (blue), they will see that 1/3 = 4/12 and 3/4 = 9/12 then summing these 2 fractions becomes a matter of simple addition. This model works will with subtraction also. Take 2/3-1/4, if you approached the number line in the same way and subdivided it into twelfths, then you would merely start at 8/12 and move left on the line 3/12 spaces.
Practice: Have students practicing subdividing number lines to create common denominators. Begin with a series of related fractions on the first day. Then move into fractions that are not as clearly connected. Focus on length when adding or subtracting to continue giving a context to what we are doing.
Lesson #3
Objective: Students will multiply fractions using arrays and explore the difference between products of whole numbers and products of their unit fraction reciprocals.
Timing: 2 - 50 minute periods
Materials: Rulers, graph paper
Opening: Write 8 x 4 on the board or the overhead. Have students discuss in their groups different ways to solve this problem. Groups should attempt to come up with at least 2 different ways. (algorithm, array(s), number line, manipulatives, drawings, etc…) Make note of the methods used. Keep chart if possible. Have groups share out in front of the class. Discuss the relationship between a product and its factors.
Choose a representation of each type of solution/process to display in front of the class. End the displays with an array. If no one has drawn one, do it yourself. Ask the students if they recognize this method. Go into detail explaining how the array represents a multiplication problem. The array below is an example of this problem.
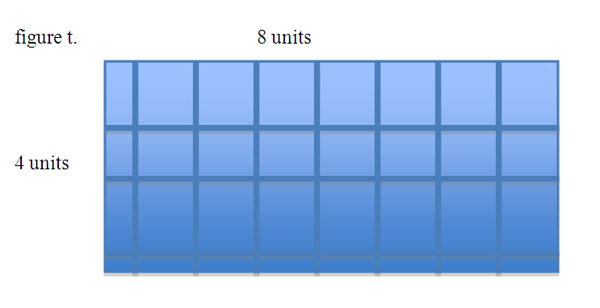
To solve a problem like this, students will need to create a grid by subdividing a rectangle into 8 parts vertically, (this can be done with precision by measuring out an 8" long line, then subdividing each inch,) and then dividing the rectangle horizontally into 4 parts( each 1 in. long ). This gives you a grid of 32 squares, or 8 x 4 = 32. Have students practice this type of solution a few more times and share drawing in front of the class.

Ask them to compare and contrast the similarities and differences between the 8 x 4 array and the 1/8 x 1/4 array. What can you say about the individual factors we are multiplying? (reciprocals). What do you notice about the products. Continue questioning until someone gets to the idea that the product of the fraction problem is smaller than each of it's factors and the product of the whole number problem is larger than the factors. Spend time discussing why this is. It will help students understand this concept, (a very important one, by the way).
Continue to work with whole numbers and their reciprocals to reinforce the idea that the product of a fraction multiplied by a fraction will give a product that is less than each of the factors being multiplied.
Appendix A
A Case for Revisiting Primary Standards in 6 th and 7 th grade classrooms
"It is not enough to know how, we must know why". This quote from a Chinese teacher interviewed by Liping Ma in her book, Knowing and Teaching Mathematics, resonates with me and needs to be a mantra for both elementary and middle school teachers. We have taught a generation of students to calculate, solve and evaluate, but we have not taught them how to think about a problem. It is rare for children to ask themselves, "what makes sense?" This is a difficult skill to teach, but revisiting concepts thought to have been mastered, and having them explain, prove and justify their solutions will go a long way in this direction.
I see 5 th, 6 th and 7 th grade students revisiting addition, subtraction, multiplication and division. I am not advocating that we re-do the same calculation lessons, but instead, open up these concepts through Number Talks, work with number lines and a deeper analysis of place value. In the Great Ideas of Primary Mathematics Seminar I was enrolled in the summer of 2011, we spent quite a bit of time working on place value activities that were quite difficult. If we focus not just on the positional aspect of this concept, but on the powers of ten and expanded notation aspects, we will be deepening our children's content knowledge without re-teaching the same old dusty algorithms.
My unit proposes to teach decimal and fraction precision using the number line. I will take students through a series of lessons that asks them to see the number line not as a place holder for whatever digits they are working with, but as a tool for understanding value of a number through linear measurement. In other words, placing numbers on a line with the distance between them in mind. In writing this curriculum and then teaching it, I must recognize that I am not, by a long shot, the first of their teachers in the 7 school years prior to my class to use number lines for students education. As I teach 7th grade Pre Algebra, it is likely that students have been exposed to, asked to create, even been taught to use number lines as a part of understanding many different mathematical concepts. With this in mind I proposed a process of deconstruction in my prospectus. This seems a bandaid (although an important one) for a more systemic issue: Teachers need to be educated/ re-educated on the potentially powerful uses of the number line and the articulation of these uses across grade levels.
Annotated Bibliography
Howe, Roger. "3 Pillars of Mathematics." Lecture, Yale National Teacher Initiative from Yale University, New Haven, July 15, 2011. Foundational information about teaching and understanding addition and subtraction operations, place value and the connections between counting numbers and measurement.
Howe, Roger. "Addition and Subtraction on a Number Line." Class lecture, Great Ideas of Primary Mathematics from Yale University, New Haven, August 16, 2011. Examples of adding whole numbers and fractions using the number line.
Bennett, Albert B., and Leonard T. Nelson. Mathematics for elementary teachers a conceptual approach. 7. ed. Boston [u.a.: McGraw-Hill Higher Education, 2008. Detailed textbook for teachers on most concepts taught in elementary mathematics. Many examples and problems for practice.
Bright, George, Merlyn Behr, Thomas Post, and Ipke Wachsmuth. "Identifying Fractions on Number Lines." Journal for Research in Mathematics Education 19, No. 3, no. May (1988): 215-232. Article reviewing a study at a school looking at student understanding of fractional values and operations with fractions by using number lines.
Chow, Wai Keung, Esther Yoon Cheng Ng, and San Ling. Discovering mathematics . Singapore: Star Publishing, 2007.
Chow, Wai Keung, Esther Yoon Cheng Ng, and San Ling. Discovering mathematics . Singapore: Star Publishing, 2009. A text for 6 th grade math students, based on the Singapore models.
Fosnot, Catherine Twomey, and Maarten Ludovicus Antonius Marie Dolk. Young mathematicians at work: constructing fractions, decimals, and percents. Portsmouth, NH: Heinemann, 2002. A book reviewing the possibilities for fractional understanding through student discovery using complex word problems for groups.
Lamon, Susan J.. Teaching fractions and ratios for understanding essential content knowledge and instructional strategies for teachers. Mahwah, N.J.: Erlbaum, 1999. A book that reviews important content knowledge for teachers about fractions, ratios and proportions. This book gives many problem sets that would be beneficial for both teachers and students.
Ma, Liping. Knowing and teaching elementary mathematics teachers' understanding of fundamental mathematics in China and the United States. Mahwah, N.J.: Lawrence Erlbaum Associates, 1999. This book examines U.S. and Chinese teacher understanding of basic math concepts such as subtraction and division of fractions.
Folsom, Amanda. "Multiplication on a Number Line." Class lecture, Great Ideas of Primary Mathematics from Yale University, New Haven, July 21, 2011. Using number lines as an alternative way to see multiplication.
Primary mathematics 4a . Standards ed. Tarrytown, NY: Marshall Cavendish Education ;, 2008. California adopted math text for 4 th grade.
Primary mathematics 5a . Standards ed. Tarrytown, NY: Marshall Cavensidh Education ;, 2008. California adopted math text for 5 th grade.
Wu, H.. "Teaching Fractions in Elementary School: A Manuel For Teachers."
www.math.berkeley.edu. http://math.berkeley.edu/~wu/fractions1998.pdf (accessed June 10, 2011). Background content information as well as many visuals for alternatives to basic algorithms.
Endnotes
- Lamon, Susan J.. Teaching fractions and ratios for understanding essential content knowledge and instructional strategies for teachers. Mahwah, N.J.: Erlbaum, 1999
- Wu, H.. "Teaching Fractions in Elementary School: A Manuel For Teachers." www.math.berkeley.edu. http://math.berkeley.edu/~wu/fractions1998.pdf (accessed June 10, 2011).
- Lumpkin, Beatrice. "ISGEm Newsletter." International Study Group on Ethnomathematics. Version Vol. 11 number 2. ISGME, n.d. Web. 22 July 2011. web.nmsu.edu/~pscott/isgem112.htm>.
- Lamon, Susan J.. Teaching fractions and ratios for understanding essential content knowledge and instructional strategies for teachers. Mahwah, N.J.: Erlbaum, 1999
- Wu, H.. "Teaching Fractions in Elementary School: A Manuel For Teachers." www.math.berkeley.edu. http://math.berkeley.edu/~wu/fractions1998.pdf (accessed June 10, 2011).
- 6 Primary mathematics 5a . Standards ed. Tarrytown, NY: Marshall Cavensidh Education ;, 2008.
- 7 Howe, Roger. "3 Pillars of Mathematics." Lecture, Yale National Teacher Initiative from Yale University, New Haven, July 15, 2011
Comments (0)
THANK YOU — your feedback is very important to us! Give Feedback
