Rationale

Common Core State Standards. Every teacher across the United States has heard of them. "Forty-three states, DC and four territories" ¹ are at various stages of implementing them. As we transition to these standards and their associated assessments, we (teachers) are looking for resources to help us make our students successful. This curriculum unit will serve as a guide for implementing the Standards for Mathematical Practice while providing meaningful instruction in the Mathematical Content Domain of High School Functions. This unit emphasizes domain and range in the study of functions and their inverses. I am writing it primarily for my precalculus students, but much of it will apply to any algebra course.

I teach in a vocational school district consisting of four high schools that draw from middle schools in all six districts in New Castle County, Delaware. We use the Core-Plus: Contemporary Mathematics in Context (CPMP) textbook series, which is an integrated math curriculum. We teach math courses in 90-minute block periods every day for one 18-week semester; students have three to four courses per semester, including their chosen career area for 90 – 180 minutes per day for the entire school year. With some exceptions for the very high and very low achievers based on a district placement test, students take two semesters of Core-Plus (1 & 2) in their freshman year, Core-Plus 3 in their sophomore year, and a "Trigonometry" transition course in their junior year. I had been teaching a traditional precalculus course for seniors, and advanced juniors for several years. For a multitude of reasons beyond my control, I started the 2013 school year with a new precalculus course guide that followed the newly published Core-Plus Mathematics: Preparation for Calculus, Course 4. I had limited access to the new textbook prior to the start of the school year, but enough to be aware of major topics incoming students had never studied. Not surprisingly, we (all district teachers teaching this new precalculus course) found more holes as the semester went along. My goal for this curriculum unit is to patch some of those holes in the content while integrating CCSS Mathematical Practice Standards.

The most glaring hole came when I began teaching how to solve trigonometric equations. First of all, my students only had a crash course in graphs of trigonometric functions. Secondly, while students have used inverse operations to solve equations, they never learned about inverse functions. Fortunately, our course alignment has been adjusted so that both of these topics will be taught in prerequisite courses. However, the most challenging part of solving trigonometric equations came when I tried to explain why there were an infinite number of solutions and how to find and denote them based on the calculator's response to sin ^-1, cos ^-1, or tan ^-1 of some value. Over the years, even my most advanced students have struggled with inverse trigonometric functions because these functions, being periodic, are not one-to-one unless the domain is restricted. As a result, I chose to write this curriculum unit to focus on domains and ranges of functions to prepare students to both operate on functions (add, subtract, multiply, divide, and compose) and find inverse functions. Throughout the unit I will use and/or design tasks that both lead to a deep content understanding of functions and incorporate the eight CCSS-M Practice Standards.

Background Content

This unit was organized by first creating a "Lesson Tree." Our seminar leader, Roger Howe, describes it as a progression of lessons "whose coherence and connectedness promote the Practice Standards." When taught in its entirety, I expect this unit to last about 10 days of 90-minute block periods; some sections may be omitted for different courses. The lessons are grouped into three major sections: "What Exactly Is a Function?", "Making New Functions From Old", and "All About Inverse Functions."

Throughout this section, I discuss mathematical concepts along with some teaching strategies. My goal for the progression is for students to first refine their understanding of what a function is and what goes into the definition of a function, learn/review/reinforce basic function families, connecting their domains and ranges to tables, graphs and formulas representing the functions. Students will learn about function operations, including composition, an operation in which it is critical to understand domain and range, in order to be able to recognize when composition is not possible for all values of the independent variable. Students will study transformations (horizontal/vertical translations, reflections, dilations) of the basic function families in the context of function composition, including their effect on domains and ranges. Finally, students will learn the requirements for the existence of inverse functions, how to adjust conditions so that an inverse can exist, and the process for finding inverses when they do exist. Again, students must be aware of domains and ranges to understand when a function has an inverse and, if it does not, how to restrict its domain and range so that the restricted function will have an inverse.

As prior knowledge, my students know a crude definition of function – for any input (x-value) there is one, and only one, output (y-value). They have used the "vertical line test" to determine whether or not a graph represents a function: if any vertical line drawn through the graph intersects more than once, then the graph does not represent a function since one value of x corresponds to more than one value of y. Students may or may not have been exposed to the terms domain and range; in either case, they can use more practice with a wide variety of examples.

Lesson 1 – What Exactly Is a Function?

The goal of this first section is to expand on students' definition of functions, emphasizing the definitions of domain, image, and range. The first step will be to solicit students' prior knowledge and use it as a review. Part of the discussion will include examples of when and how they have used or heard the phrase "something is a function of something," and questions such as, "are these statements true in the mathematical sense?" or "what do they mean mathematically?" For example, "wisdom is a function of age" implies that a person's wisdom increases as he/she gets older. However, in more precise mathematical language, this statement would mean that for every age, there is exactly one value for wisdom (I wonder what that value would be?). Additional, more valid, examples of functions might include the height of a soccer ball as a function of the time it's in the air for a given starting height and initial upward velocity, or the area of a circle as a function of its radius.

According to the NCTM book Putting Essential Understanding of Functions into Practice, a common misconception is that functions can always be written as formulas. ² However, "functions can have many representations, of which equations are just one." ³ The only requirement is that for every input, there is exactly one output. A common way of describing this relationship is that an input value "maps" to a single output value, input —> output. Therefore, any relationship that satisfies this requirement, whether it is described in words, shown as a continuous graph, as a plot of discrete points, as sets of ordered pairs, as values in a table, or as a formula, can represent a function.

A key feature of functions is that they must be defined for specified input values, which defines the domain of the function. For a formula, the implicit domain is all input values that make sense. However, the domain may also be stated as a specific set of values or as some interval (i.e. all integers greater than zero, or the interval [0, 10]). The set of all output values of the function, for all points in its domain, is called the image of the function. Since it can be difficult to know the image, we can name a larger set that contains all the output values of the function. This larger set is called the range. For convenience, we often let the range be all real numbers. The conditions on the range are looser than those on the domain. The function must be defined for every point in the domain, but the range only has to contain the values of the function - not every point in the range has to be an output value of the function.

It is important to emphasize that changing the domain changes the function. Consider, for example, A(Θ) = sinΘ over the interval [0,90°] . The sine function is always increasing over this interval; its image is [0, 1]. But, if we consider the same function over the interval [90,270°], it is always decreasing; its image is [-1, 1]. And if we take the domain to be [0,360 ^o], the sine function is multivalued: it takes every value except ±1 twice, and takes the value 0 three times. Thus, although we may refer to all three functions by the same name, "sine", we are actually dealing with different functions that have different properties.

Lesson 2 – Making New Functions From Old

Part 1 – Function Arithmetic

According to Scott Steketee and Daniel Scher, "students have difficulty thinking of functions as objects in their own right, subject to mathematical manipulation." ⁴ In this lesson students will first learn to manipulate functions using basic arithmetic operations – addition, subtraction, multiplication and division. I will not discuss the skills themselves here because they are the same as those studied with respect to polynomials. What will most likely be new for my students are the notation and the need to consider the implicit domain and range in order to know whether the operation is possible. For example, let f(x)=2x and g(x)=√x. The implicit domain of f(x) is (-∞,∞) but the implicit domain of g(x) is restricted to [0,∞). Therefore, the sum (f+g)(x)=2x+√x can only be computed over the domain [0,∞), the interval where both functions exist. For the same reason, the image of (f+g)(x) is also restricted to [0,∞). Students will need explicit practice with division of functions, as in (f⁄g)(x)=2/√x because the domain must exclude any value that makes the divisor (denominator) equal to zero, which in turn may also restrict the range. They should constantly ask themselves, "Are there any new numbers that don't work?" In this division example, the domain and range are both restricted to (0,∞) to further exclude dividing by zero.

Part 2 – Function Composition

Composition is a useful operation performed with functions, and is analogous to substituting values or expressions for variables. It is one of the "crucial prerequisites for mastery of related topics such as transformations of … families of functions, and inverses of functions," ⁵ topics addressed within this curriculum unit. For two functions defined as h(x)=√x and q(x)=1-x^2, the composition function (h*q)(x), read as "h of 'q of x'." is computed by h(q(x) ). The composition operation requires us to use x as the input for function q. The corresponding output, q(x), then becomes the input for function h. Using the functions defined above, h(q(x) )=h(1-x^2 )=√(1-x^2 ). Since its very definition uses the output of one function as the input for another in function composition, it is critical to consider the domains and images to determine whether the composition is even possible. Again, referring to the two functions above, the image of q is (-∞,1], yet the domain of h is [0,∞). Therefore, the composition is only defined on the interval where 1- x^2≥0, that is, on [-1,1].

It is straightforward to see that function composition, in general, is not commutative, although it is commutative in some cases discussed later. Using the two functions defined above, (q*h)(x)=q(√x)=1-(√x)^2=1-x, which is different from √(1-x^2 )=(h*q)(x). I demonstrate the lack of commutativity here, but I think students should explore many examples of function composition to reach this conclusion themselves.

Staying with arithmetic properties, function composition is always associative. The Associative Property refers to how three objects are grouped. In the case of three functions, A, B, and C, the Associative Property of Function Composition states A*(B*C)=(A*B)*C. As justification, recall that we defined (B*C)(x) = B(C(x)). Then (A*(B*C))(x)=A(B(C(x) )). Likewise, (A*B)(x) =(A(B(x)) so

((A*B)*C)(x)=(A*B)(C(x))=A(B(C(x) )).

We see that grouping does not affect the result of function composition. As an example, let's use f(x)=x+2 and g(x)=x^3, and h(x)=4x and compare (h*(g*f) )(x) to ((h*g)*f)(x). First, (g*f)(x)=(x+2)^3 so (h*(g*f) )(x)=h((x+2)^3 )=4(x+2)^3. Then (h*g)(x)=4x^3, so ((h*g)*f)(x)= 4(x+2)^3, the same result. Fortunately, all three functions are defined for all real numbers, so the composition is also defined for all real numbers, without restrictions.

When I teach function composition, I think it is helpful for students to see real-life examples. An example could be as simple as calculating your salary for a week. Suppose a worker is paid $9.00/hour for the first 40 hours, and "time-and-a-half" for overtime beyond 40 hours. We can write a function P(x)=1.5(9.00)x to represent the overtime pay for x hours of work. For a week the worker works more than 40 hours, her overtime hours can be calculated by the function H(x)=x-40. To find her overtime pay directly, the two functions can be composed: (P*H)(x)=1.5(9.00)(x-40). The domain for H(x) is [40,∞) to represent only overtime hours; if the lower limit were less that 40 she would be paying her employer to work! The image is then [0,∞) which is an acceptable domain for function P(x) yielding an image of [0,∞). We could argue that there is an upper limit to the number of overtime hours, and therefore a maximum possible pay, as well.

There is an NCTM Illuminations activity entitled "Successive Discounts," in which two discounts are applied to a pair of jeans. There is a coupon for $5 off and a 25% off sale at the store. The activity connects algebraic expressions, graphing, domain (including using the domain to set the Window on the graphing calculator), function composition, and mathematical practice standards (MP5 and MP7) to determine which order of discounts results in the lower price. For C(p) representing the price after the coupon and S(p) representing the price after the discount, questions such as "What does C(S(p)) mean in words versus what does S(C(p)) mean?," and "Is there a difference between the values of the two compositions?" can help students practice composition as an operation and recognize that it is not always commutative. If the discussion includes the reason for the difference between the values, students are boosting number sense and reasoning abstractly (MP2). Supplying students with examples such as this, and asking them to create their own will help them understand the operation of function composition, including its meaning and the need to consider domain and image.

Part 3 – Transformations

Transformations of the function families is a common topic in precalculus. In this lesson, I want students to understand that these transformations (translations, reflections, dilations) are function compositions. They will investigate single transformations as well as multiple transformations, always considering the domains and ranges of the original and the transformed functions. As they investigate, students should also look for patterns and make connections with previously studied math topics.

Horizontal translation can be defined as the mapping, Tt, x → (x – t) where t represents the number of units to shift in the x-direction. When t is a positive number, the input, x, is reduced (shifted to the left by subtraction); however the graph appears to shift to the right, as seen in Figure 1. When t is a positive number, the reverse happens. The composition can be written as (f*T _t ). Thus, for the function f(x)=x^2 we get f(x-t)=(x-t)^2. Students should select varying values for t and explore tables and graphs of the original and transformed functions to see the effect of the translation on domain and image.

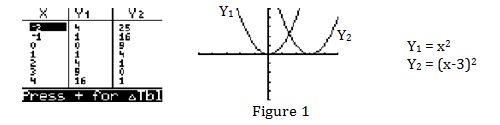
If the process is repeated first for the absolute value, cube, cube root, linear and exponential function families, and later for square root and reciprocal functions, students can discover through observation that horizontal translations, being pre-composition, only affect the domains of square root and reciprocal functions. Hopefully they make the connection that these are the functions that had restricted domains (a lower limit or undefined value(s)) initially. As I have said to my students, infinity plus five is still infinity, so a horizontal translation will not alter the implicit domain (-∞,∞). For the translated functions f(x-t)=√(x-t),1/(x-t),and 1/(x-t)^2 , the value of the undefined point(s), or interval, is shifted t units to the right for positive values of t. For negative values of t, the translation is to the left. I found an activity in the August 2010 issue of Mathematics Teacher magazine that emphasizes the fact that it is the input value, x, that is decreased by t units for x → (x – t); decreasing by a negative t value (subtracting a negative) is the same as increasing by t units. The activity uses a coordinate grid covered by a transparency with the graph of any function sketched on it. For example, if x → (x+3), the grid underneath (representing the input) would be increased by 3 units (shifted to the right); the effect is the function appears to move 3 units to the left, as students observed. Not to forget about the image in horizontal translations, the interval for the image is not altered at all.

Vertical translation, is defined as g(x)=f(x)+c. In this case, a value, c, is added to the output of the original function; vertical translation is post-composition with T-c, written as (T_(-c)*f). Again, assigning a value for c in a mapping for all of the function families, students can observe the transformation using technology. Since the value c is added to the output, it has no effect on the domain of each function. A positive value of c increases the output, shifting each point up c units; a negative value shifts points down. Vertical translations shift the image of functions that have a lower boundary by c units: f(x)+c=x^2+c,a^x+c,|x|+c,√x+c,1/x^2 +c. The image for f(x)+c=1/x + c becomes (-∞,c)Ã"(c,∞), and the image for f(x)+c=sin(x)+c and cos(x)+c is [-1+c,1+c].

The final function transformation I will discuss uses dilation, Dd. A dilation or "stretch" is defined by the mapping

D_d:x→d⋅x,

where d is a (scale) factor multiplying the input x ("stretch" occurs for |d| >1, and "shrink" occurs for |d| <1). A vertical "stretch" is achieved by post-composing a function with D _d:

f→g, where g(x)=(D _d*f)(x)=d⋅f(x)

A horizontal stretch is achieved by pre-composition with D _d^(-1):

f→g, where g(x)=(f*D _d^(-1))(x)=f(x/d).

As with translation, pre-composition produces the opposite effect from what you might expect.

Furthermore, negative values of d produce reflections. The pre-composition dilation (f*D _-1 ) reflects the graph across the y-axis, while the post-composition dilation (D _-1*f) reflects it across the x-axis. Observations of graphs of function families and their horizontal reflections f(-x)=(-x)^2,|-x|,1/(-x)^2 ,-x,√(-x),(-x)^3,a^(-x),and 1/(-x) can lead to a lively discussion about why some functions look like they don't change (symmetry with respect to the y-axis) and how a function rule could help predict which functions they are. With the exception of f(-x)=√(-x), the domains and ranges are not affected by the reflection; however the domain of the square root function changes to (-∞,0] to ensure that the values inside the radical are non-negative. I would also encourage discussion about functions having symmetry about the origin, for which the combination of reflections across the x- and y-axes (both horizontal and vertical reflection) reproduce the original function (no visible change). It is a precursor to the concept of odd and even functions needed for calculus.

Function transformations can be performed in succession. Dilations composed with dilations mimic multiplication. The result is dilation of the product of both dilations: D _d*D _e=D _de. Translations composed with translations mimic addition. The result is translation of the sum of both translations: T _a* T _b=T _(a+b). Another example of multiple compositions can be found by composing dilation with translation. This combination of transformations forms a special category of functions called affine functions (ax +b, another name for linear functions). If the first transformation is a dilation of magnitude 3, D3, and the second transformation is a vertical shift of 2 units down T2, we have the composition (T ₂*D ₃ )(x)=3x+2. If we repeat the same composition, we will get (T ₂*D ₃ )(3x+2)=3(3x+2)+2=9x+8. However, if we reverse the order of composition to translate and then dilate, we get (D ₃*T ₂)(x)=3(x+2)=3x+6. Composing again, with the same sequence of transformations, we get (D ₃*T ₂)(3x+6)=3(3x+6)=9x+18. What we notice about the composition of affine functions is that it produces another affine function. However, the order of the composition can change the resulting function: composition of affine functions is not commutative, although composition of dilations by themselves is commutative, and composition of translations by themselves is commutative. The domain and range for affine functions are all always real numbers.

Lesson 3 – All About Inverse Functions

Part 1 – More Definitions: Identity Function, One-to-one Functions, Inverse Functions

This lesson must begin with a definition of the Identity Function. It may be helpful to remind students about the Identity Properties for Arithmetic – there exists a number when added to a such that the sum is equal to a (a + 0 = a), and there exists a number when multiplied by a such that the product is equal to a (a ⋅1 = a). In other words, there is a number that can be added or multiplied that keeps the original number the same. Along the same line, for each set, its Identity Function is the function that returns an output equal to its input (f(x)=x); an Identity Function keeps the input value the same.

There is yet another new term for students to learn in order to finish this unit: one-to-one. A function is said to be one-to-one if each different point in its domain maps to a different member in its image. Many students think, incorrectly, that this is a condition to be a function. For example, the graph of f(x)=2, a horizontal line, is a function, but it is not one-to-one because the domain may contain an infinite number of values, yet the image contains only the value 2.

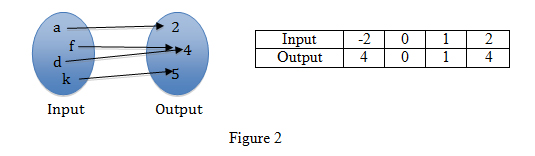
Both the relationships shown in Figure 1 are functions that map each input to exactly one output. However, since for many output values there are two different inputs that map to the same output, the functions are not one-to-one. The one-to-one relationship is, in fact, a special condition of functions that allows its inverse to be a function.

Armed with lots of definitions and practice with functions, domains, images and ranges and compositions thus far, students are ready to learn about Inverse Functions. Students have been working with inverse operations for years as a way to solve algebraic equations and unknown parts of fact family statements. They may think of inverses as"undoing, and that's not a bad place to start. The precise definition is this: for a function f, with domain D and range R, that maps x→y, an Inverse Function, denoted f^(-1), maps y→x such that function composition in both directions gives the Identity Function. In other words, both (f*f^(-1) )(y)=y and (f^(-1)*f)(x)=x. It is critical to keep track of the domain and range when working with inverse functions because the inverse function, f^(-1) (y), takes values from the image of f(x) as its domain, so f^(-1) (y) must be defined over the interval of the image. In other words, the domain of f^(-1) is R, and the range of f^(-1) is D. In addition, the inverse can only be called a function if each member of its domain (the image of the original function) maps to exactly one value in its image (the domain of the original function). Furthermore, for an inverse to exist, the range must equal the image; the range may first be limited to be the image, if necessary, to construct an inverse function.

One very practical example of an inverse function is converting between Fahrenheit and Celsius temperatures. (Note: These are affine functions of each other.) In my readings, I learned that the procedure many of us learned in school – switch the x and y and then solve for y – can lead to confusion because the variables change their meaning. ⁶ For example:

Instead, it is best to use variables to represent the same unknown throughout the process. Then, to find the inverse function, we can simply solve for the dependent variable, whatever that may be. ⁷

As an example: Mike is on a business trip in Europe and sees a temperature reading of 20°C on the television. He knows he will want a jacket if the temperature is below 65°F. The conversion formula Mike knows is C=f(F)=5/9(F-32). Find the inverse function, F=f^(-1) (C), to find the temperature in °F to determine if Mike needs a jacket. To begin, we must recognize the conversion formula has, as its domain, temperature in °F, and, as its range, temperature in °C. To find the inverse function, we will take temperature, C, in °C as the independent variable and domain and "solve for F, the dependent variable." Since C= 5/9(F-32), we can begin by dividing both sides of the equation by 5/9, which is equivalent to multiplying by 9/5. Now 9/5 C=F-32. Adding 32 to both sides of the equation leads to 9/5 C+32=F, which is F as a function of C! So, the inverse function is F=f^(-1) (C)=9/5 C+32. If we substitute C = 20, we get f^(-1) (20)=9/5 (20)+32=68°F. That means Mike should be all right without his jacket. Just to emphasize the fact that compositions of inverse functions produce the identity function, let's check: (f*f^(-1) )(C)=5/9 ((9/5 C+32)-32)=C and

(f^(-1)*f)(F)=9/5 (5/9 (F-32) )+32=F.

In the activities in Lesson 3 students will begin by identifying one-to-one functions from tables and graphs to reinforce the conditions under which a function is invertible (i.e. the inverse is also a function). As suggested in the CCSS-M High School Function Content Domain, Building Functions B.4.C, for those functions that are invertible, they will then read values of an inverse function from a graph or a table. There may or may not be discussion about the "horizontal line test." I, myself, have been convinced by my readings to avoid teaching these tricks as the way to determine whether a graph represents a function. It is limiting in that it only tests whether y is a function of x when it may be okay to refer to a relationship between x and y where x is a function of y.

As students work through the Lesson 3 Activities, I want them to focus on three key ideas:

1. Begin with y as a function of x (y=f(x)), and solve for the dependent variable, x, to get the inverse function as a function of y (x=f^(-1) (y) ).Students will consistently record the domain and range for both the original function and its inverse to look for patterns and to ensure the inverse is defined for all members of its domain ( image of the original function).
2. The procedures for solving for inverse functions are the same as for solving algebraic equations. Students should think of finding the inverse function by doing the inverse of each operation in the reverse order of the original function. ⁸
3. Compare the graph of an inverse function to that of the original function. After students compare several graphs of functions and their inverses they should begin to recognize them as reflections across the line y = x. However, it can be incorrect to graph both functions on the same graph because the horizontal and vertical axes also reflect and represent different variables, but drawing the line y = x on both graphs can still help to see the reflection. ⁹

Finally, according to the CCSS-M High School Function Content Domain, Building Functions B.4.D, students should be able "produce an invertible function from a non-invertible function by restricting the domain." This is the culmination of this curriculum unit. First students must recognize when and why a function is invertible. They must understand how to find an inverse function, and they must have a solid understanding of domain and range in order to restrict the domain to produce the invertible function. In many contextual problems, the domain is restricted naturally. For example, the area of a circle as a function of radius, f(x)=A=Πr^2, graphed over its implicit domain of all real numbers is a parabola, and not invertible. However, the practical domain is only positive numbers (since the radius is a positive quantity), which makes the function invertible.

In the more general case, let y=f(x)=x^2. The implicit domain and image of f(x) are (-∞,∞) and [0,∞), respectively. Let x=g(y)=f^(-1) (y)=√y with both the implicit domain and image being [0,∞). To verify that g(y)=f^(-1) (y), we must show that both compositions (f^(-1)*f)(x)=x and (f*f^(-1) )(y)=y are true. Let's check: (f^(-1)*f)(x)=√(x^2 )=x is true for x≥0. However the domain of x^2 includes negative numbers, but √((-5)^2 )≠-5 since -5 is not part of the image of the square root function. Since the composition (f^(-1)*f)(x)=x is not true for all values in its domain, g(y) is not the inverse of f(x). Let's check composition in the other direction: (f*f^(-1) )(y)=(√y)^2=y is a true statement for all values in the domain of g(y). We notice that the output from √y is a restriction on the implicit domain of f(x)=x^2 to x≥0. This is exactly why and how we can restrict the domain of the squaring function to make it one-to-one and invertible. Of course, the restriction could also be any smaller interval within the domain [0,∞). Figure 3 illustrates how restricting the domain of f(x)=x^2 to [0,∞) makes it an invertible function. It also shows the relationship between the graphs of f(x) and f^(-1) (x).

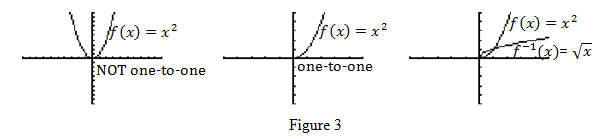
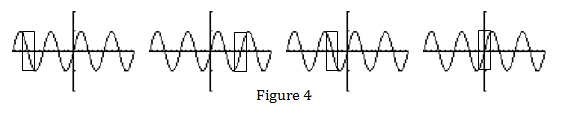
One last example to demonstrate the need to restrict a domain in order to enable a function to have an inverse is with trigonometric functions. Let's work with f(Θ)=sinΘ which has a domain of (-∞,∞) and image of [-1, 1]. Students familiar with the unit circle, know that the sine function is not one-to-one because there are elements in its range that correspond to more than one angle, Θ, in its domain. For example, f(Π/6)=f(5Π/6)=f(13Π/6)=1/2. In fact, every time we go around the circle, the values of sine and cosine repeat. As a result, the domain must be restricted to an interval that will make it one-to-one. To make the inverse function as useful as possible for solving trigonometric equations, its domain should include the full range of values for sine, namely [-1, 1]. If we consider the graphs in Figure 4, we see that there could be an infinite number of possibilities, but the standard convention among mathematicians is to use the restricted domain [-Π/2,Π/2], the last one on the right, because we like to consider angles to be acute.

STRATEGIES, AS THEY RELATE TO CCSS-M PRACTICE STANDARDS

In the Rationale Section, I stated that I would incorporate the eight CCSS-M Practice Standards into this unit. As we discussed in our seminar, the Practice Standards are not necessarily meant to be taught explicitly; they are more habits that we want to develop in our students to make them successful. Toward that goal, the carefully planned progression of activities, in the lessons detailed above, will help students achieve the first two Math Practice Standards (MP1 and MP2), "Make sense of problems and persevere in solving them," and "Reason abstractly and quantitatively." By starting with students' prior knowledge, making connections to the vocabulary in other areas of their lives, and from previous math topics, students should have enough confidence to get started. The discussion around inverting functions – getting a clear idea of what invertibility should mean, and the need for one-to-oneness, will require substantial sense-making by students. Students will work collaboratively through most of the unit, always discussing and comparing their observations and results, and making conjectures to test further. These small group discussions and conjectures attend to MP3, "Construct viable arguments and critique the reasoning of others." As students gain confidence within small groups they will be asked to participate in full class discussions, and critique or justify the reasoning of their classmates. The fourth Math Practice Standard, "Modeling with mathematics," is addressed through some of the situations in the tasks and by testing conjectures students make along the way. The next two standards, MP5 and MP6, "Use appropriate tools strategically" and "Attend to precision" are the most strongly addressed. For example, students will use graphing calculators or computer software to make observations and conjectures. Requiring students to state the domain and range throughout the entire unit is one way to "attend to precision." Students will "Look for and make use of structure," according to MP7, in nearly every activity in this unit: connecting definitions to graphs, tables, and formulas, connecting transformations to composition and to geometry, connecting inverse operations and inverse functions, and the structure in graphical representation of functions and their inverses. The last Math Practice Standard, MP8, recommends students "Look for and express regularity in repeated reasoning." This standard states, "As they work to solve a problem, mathematically proficient students maintain oversight of the process, while attending to the details. They continually evaluate the reasonableness of their intermediate results." Again, the lesson tree design will help students stay focused on the key understandings for functions, and question whether something new is reasonable based on what they have learned along the way.

Classroom Activities

Lesson 1 – What Exactly Is a Function?

I expect this lesson to take two to three 90-minute block periods. At the end of the lesson, students will be able to identify functions from multiple representations and specify the domain and range, and also the image, for each.

Activity 1- Introduction

To begin, I will use the "Function Wall" Activity from the NCTM book Putting Essential Understandings of Functions into Practice ¹⁰ to lead students to understand the definition of function. (Because it is not an original activity, I will only explain the basics here.) First, place letters A through D at different places around the room. Then assign characteristics to each letter, and tell students to stand by the letter that matches their response to a question. For example, the question may be "What is your age?" If A represents "over 18 years," B represents "over 17 and up to and including 18 years," C represents "over 16 and up to and including 17 years," and D represents "under 16 years," then each student should go to one of the letters A through D without confusion. In contrast, if the question is "Who lives in your home with you?" and A represents "mother," B represents "father," C represents "brother," and D represents "grandparent" then there will most likely be confusion because students may live with both parents, or may live with a mother and brother. The fact that there is confusion means the relation between the student and with whom he/she lives is not a function.

A second introductory activity that I will adapt to help students recognize functions from different representations – words, table, graph, or formula - is from the same book as above. Each problem gives two set names and asks whether one set is a function of the other. For example, set A is named "Date", and set B is named "High temperature of the day." Students can be asked whether set A is a function of B, i.e. whether the date is a function of the high temperature. Since more than one date can have the same high temperature, the relation is not a function. Students can also be asked whether set B is a function of A, i.e. whether the high temperature is a function of the date. The answer is yes, because there can only be one high temperature for a given date. Asking about the same two sets in two different ways should help students really focus on the definition of function.

Activity 2 – Working with Domains

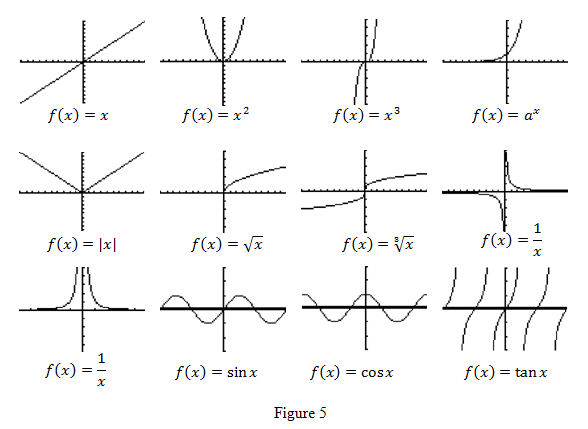
To start, students will look at graphs of familiar function families (linear, exponential, square, cube, square root, etc.). They will record the definitions of domain, implicit domain, range and image, and identify the implicit domain and estimate the image from the function family graphs shown in Figure 5. In particular, I want them to recognize how maximum, minimum, and undefined values in the domain and image appear in the graphs. Finally, working in small groups so they can discuss observations and sort out the definitions in different scenarios, students will complete the Lesson 1, Activity 2 worksheet given in Appendix C.

The closing activity for this lesson comes from the March 2013 issue of Mathematics Teacher. ¹¹ It contains a set of 37 cards containing equations, tables, graphs, and written descriptions of scenarios. The general instructions are "Sort the cards and be prepared to explain your categories with others." Again, students will work in small groups. The sorting can be as basic as function and non-function categories, or it can distinguish function families (linear, exponential, periodic, etc.). There are some cards that are included to generate discussion. For example, one card has "y ⁴ = x" printed on it. Some students may claim it does not represent a function, but since the directions do not specify that y must be a function of x, it is worth pointing out that, in this case, x is a function of y. Another example is a card that contains a table of x and y values that appears to follow the rule y = 3x with the exception of one outlier. Since every x value in the table maps to a single y value, the table does represent y as a function of x. It is good reinforcement for students to remember that functions do not necessarily need to be written as formulas.

Lesson 2 – Making New Functions From Old

I expect this lesson to take three to four 90-minute block periods. At the end of the lesson, students will be able to calculate and state the domains for the sum, difference, product and quotient of functions from tables, graphs and formulas. They will be able to write and perform function composition, and describe function transformations as function composition.

Activity 1 – Function Operations: Arithmetic

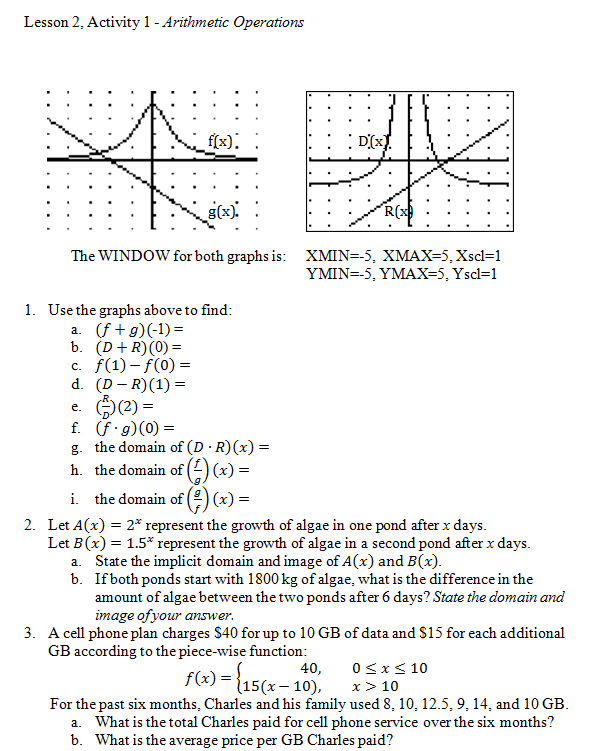
Textbooks typically provide practice with the basic function operations of addition, subtraction, multiplication and division, so I won't include examples here. In the interest of precision, I will insist that my students record the domain for each original function and the final result whenever appropriate. I have included some examples of performing operations from values found in graphs (without the formula provided), along with a sampling of word problems on the Lesson 2, Activity 1 worksheet in Appendix C.

Activity 2 – Function Operations: Composition

To introduce the concept of function composition, I will use real-world problems that students can solve by performing multiple steps without using functions explicitly, including some in my Core Plus 4 textbook. For example, suppose the cost to rent the local fire hall is $250. If they charge $15 per person for food plus an 18% gratuity on the total bill, what is the total cost for the event? Students can calculate the total cost given the number of attendees, or they can write two (affine) functions and use them in succession. The two functions are f(n)=250+15n, for the room and food, and T(f)=1.18f=D_1.18*f for the total cost, including gratuity. It should not be a stretch to combine these two functions by composition, essentially substituting f(n) into T(f); only the notation (T*f)(n)=T(f(n) )=1.18(250+15n)=295+17.7n will be new. We also need to discuss domains and images for composition. Since we are substituting f(n) into T(f), the image of f(n) must be part of the domain of T(f). In this case, since we can multiply any number by 1.18, the composition can be performed.

Illustrative Mathematics "The Canoe Trip" ¹² task presents a situation in which the speed of the current of a river affects the paddler's speed. By completing a table of values, students recognize the pattern and write equations for the paddler's actual speed and the time to complete the trip. If R(c) is the paddler's speed as a function of current speed, and time to complete the trip is a function of the paddler's speed, T(R)=d/R for a specified distance, d. Therefore, T(R(c)) gives the time as a function of current speed. Once again, discussion about the domains and images of both functions is required to force students to consider feasible inputs and outputs for all functions. Resources for additional word problems that apply function composition are listed in Appendix B.

Somewhere in the middle of the lesson, I will have students practice composition, as a skill only, with a relay race game that I found at the BetterLesson website. ¹³ For the game, a team of students divides a list of functions (written as formulas on cards or on the board). The teacher calls an input number and the 1 ^st student in each team evaluates f(n) and passes the output to the next person. The 2 ^nd student evaluates g(f(n)), the 3 ^rd evaluates h(g(f(n))), etc.

After a few rounds of the relay race the energy level in the classroom should be raised enough that students can move on to examples of compositions that cannot be performed for all values of the independent variable. As I demonstrated in the Background section, when the image of one function differs from the domain of the other, composition may not be possible, or it may exist only for a restricted interval. Practice is provided on the Lesson 2, Activity 2 worksheet in Appendix C.

Activity 3 – Transformations as Compositions

In this activity, I will build on textbook activities that have students explore and practice transformations of basic function families. Specifically, I will emphasize how the procedure for "completing the square" to rewrite a quadratic expression helps us visualize transformations to f(x)=x^2. Let's start with q(x)=3x^2-4x-8. The first step is to divide the first two terms by the leading coefficient to get q(x)=3(x^2-4/3 x+?)-8. The question mark is waiting for the value that will form a perfect square in the parentheses – ½ the coefficient of x, squared – (2/3)^2=4/9. We need to keep the expression the same, so we apply the Identity Property of Addition to get q(x)=3(x^2-4/3 x+4/9-4/9)-8=3(x^2-4/3 x+4/9)-3" 4/9-8=3(x-2/3)^2-28/3. From this form of the quadratic function, we can see the transformations: horizontal shift to the right 2/3 units, vertical stretch factor of 3, and vertical shift down 28/3 units. Furthermore, we can write these transformations as a composite of the following transformations: (1) f(x)=x^2; (2) g(x)=(x-2/3); (3) h(x)=3x; (4) j(x)=(x-28/3); (5) q(x)=j(h(f(g(x) )).

Unless the domain is restricted based on the problem, the domain for all of these transformation functions is (-∞,∞). The image for q(x) is [-28/3,∞), as determined by the vertical translation. Since vertical translation is the last transformation, performed on the output, it does not restrict the domain of the other transformations. I will provide abundant practice with this procedure to determine the transformations of quadratic functions. The task entitled "Building an Explicit Quadratic Functions by Composition" on the Illustrative Mathematics website provides additional practice, and I will create additional problems similar in structure for other function families. For still more practice, I will alter the instructions for the Illustrative Mathematics task "Domains" to ask students to write the list of transformations starting with a transformed function and working backwards to the basic function family. Of course, I will still require them to state the domain for each transformed and basic function. At the end of these activities I will assess students' ability to use function composition to perform transformations.

Lesson 3 – All About Inverse Functions

I expect this lesson to take approximately three 90-minute block periods. At the end of the lesson, students will be able to define and recognize one-to-one functions, define the Identity function, find and verify (simple) inverse functions by composition, and restrict the domain of a function to make it invertible.

Activity 1 – What Types of Functions Have Inverses?

As a Warm-up activity, I will ask students to solve the following equations for x:

Once students have the solutions, I will ask this series of questions to lead them to understand the definition and the significance of one-to-one functions:

1. Which of the equations above have more than one solution? (#2, 5, 8)
2. If the right-hand side of each equation were replaced with y, what do the graphs of these functions look like?
3. For equations #2, 5, & 8, is y a function of x? Explain. Is x a function of y?

This extended warm-up, will provide examples, and non-examples, to informally assess student understanding of one-to-one functions: each input leads to a different output.

Next, I will ask students questions like "What is the additive inverse of 5? -2? 0?" and "What is the multiplicative inverse of 5? -2? 4/3?" to refresh their memories on the term inverse. Then, just like a number plus its additive inverse equals the additive identity, 0, and a number multiplied by its multiplicative inverse (reciprocal) equals its multiplicative identity, 1, a function composed with its inverse equals the Identity Function. The Identity function is f(x)=x, which is the line that forms a 45° angle with the x-axis. Before moving on, students should practice recognizing one-to-one functions and composing functions to verify that they are inverses. Sample problems are given on the Lesson 3, Activity 1 worksheet in Appendix C.

Activity 2 – How to Find an Inverse

With vocabulary taken care of, students are now ready to practice finding inverse functions. First they will find inverses in context so that the variables have meaning and to help understand the notation f^(-1) (y)=x for f(x)=y, and then for any algebraic formula. I will refer back to the warm-up problems in Activity 1 to help students make the connection that they already know how to use inverse operations to "undo" and solve algebraic equations, and that inverse functions "undo" functions. Therefore, when solving equations of one-to-one functions, we can work backwards (undoing) from an output to find its corresponding (only) input. With practice, students should recognize that all (non-constant) affine functions have inverses, and finding them is like solving linear equations. Students will state the domain and image for simple functions and their inverses, looking for any relationships between them. When appropriate, students will graph both the function and its inverse, adding the line representing the Identity function, f(x)=x. Students will also find the intersection between a function and its inverse to recognize that it always lies on the line representing the Identity function. Sample problems beyond typical textbook problems are given in Appendix C on the Lesson 3, Activity 2 worksheet.

Activity 3 – How to Make a Function Invertible

Several problems in previous activities (#2, 5, 8 in the warm-up for Activity 1, D(x) and P(x) on the Lesson 3, Activity 1 worksheet, and several of the contextual problems on the Lesson 3, Activity 2 worksheet) may have already generated discussion about restricting domains so that a function has is invertible. Students most likely have observed that graphs of parabolas and absolute value are not one-to-one, and therefore, not invertible as is. General formulas with squares (or higher degree polynomials) do not have inverse functions, either. However, if we restrict the domain, they may become invertible. In this activity, students should go back to all previous activities to find functions for which there was no inverse, and restrict the domain so that there is. Additional problems such as "Find a domain for f(x)=3x^2+12x-8 on which it has an inverse" followed by class discussion would provide informal assessment of students' understanding. The discussion should include comparison of students' restricted domain and justification (critique) for its validity. Such a discussion will demonstrate that restrictions are not unique; I will present additional options for domains if students don't do it naturally. This discussion leads naturally to my ultimate goal for the unit – restricting the domains for trigonometric functions so that they are invertible. I will end this unit here with the belief that my students are better prepared to understand inverse trigonometric functions and how to use them to solve trigonometric equations.

Appendix A - Common Core State Standards for Mathematics (CCSS-M)

This curriculum unit addresses all eight of the CCSS Mathematical Practice Standards as outlined in a previous section. It also addresses the CCSS-M Content Standards for High School Functions, Building Functions:

CCSS.MATH.CONTENT.HSF.BF.A.1B – Combine standard function types using arithmetic operations.

CCSS.MATH.CONTENT.HSF.BF.A.1C – Compose functions.

CCSS.MATH.CONTENT.HSF.BF.B.3 - Identify the effect on the graph of replacing f(x) by f(x) + k, k f(x), f(kx), and f(x + k) for specific values of k (both positive and negative); find the value of k given the graphs. Experiment with cases and illustrate an explanation of the effects on the graph using technology.

CCSS.MATH.CONTENT.HSF.BF.B.4A - Solve an equation of the form f(x) = c for a simple function f that has an inverse and write an expression for the inverse.

CCSS.MATH.CONTENT.HSF.BF.B.4B – Verify by composition that one function is the inverse of another.

CCSS.MATH.CONTENT.HSF.BF.B.4C – Read values of an inverse function from a graph or a table, given that the function has an inverse.

CCSS.MATH.CONTENT.HSF.BF.B.4D – Produce and invertible function from a non-invertible function by restricting the domain.

Appendix B – Resources and Bibliography

Illustrative Mathematics website (www.illustrativemathematics.org) is a rich source of problems. The website can be searched by grade level and by CCSS-M standard. I found several tasks for Function Composition and Inverses by searching in "HS Functions."

I found some tasks on the NCTM Illuminations website (http://illuminations.nctm.org/). Search on Common Core Math Standards, grades 9-12, "function composition."

I found several lessons that I will use or adapt by searching on the Better Lessons website under the Common Core tab, under HS Functions, Building Functions (or others) (http://cc.betterlesson.com/common_core).

Boas, Ralph. "Inverse Functions." The College Mathematics Journal 16, no. 1 (1985):

42-47. www.jstor.org/stable/2686627 (accessed July 8, 2014).

Edenfield, Kelly. "The Common Core and Inverse Functions." Mathematics Teacher

105, no. 9 (2012): 672-676. Justification for teaching inverses despite being a

CCSS-M (+) topic; they are necessary for coherence.

Faulkenberry, Eileen Durand, and Thomas J. Faulkenberry. "Transforming the Way

We Teach Function Transformations." Mathematics Teacher 104, no. 1 (2010):

29-33. Demonstrates the use of transparencies to demonstrate the difference

between transformations of the input versus the output variable.

Garman, Brian. "Inverse Functions, Rubik's Cube, and Algebra." The Mathematics

Teacher 78, no. 1 (1985): 33-34, 68. www.jstor.org/stable/27964346 (accessed

July 8, 2014).

Hall, Becky, and Rich Giacin. "Exploring Function Transformations Using the

Common Core." Mathematics Teacher 107, no. 2 (2013): 132-137. Connects

function transformations to geometric transformations.

Hillen, Amy, and LuAnn Malik. "Sorting Out Ideas about Functions." Mathematics

Teacher 106, no. 7 (2013): 526-533. Describes a sorting activity to strengthen the

concept and definition of function.

Hurwitz, Marsha. "Understanding the Composites." The Mathematics Teacher 89, no.

2 (1996): 116-117. Includes tasks to practice composition of functions.

Ronau, Robert N., Dan Meyer, and Terry Crites. Putting Essential Understanding of

Functions into Practice. Reston, Va.: National Council of Teachers of Mathematics,

2014. Provides activities and scenarios for teaching functions.

Steketee, Scott, and Daniel Scher. "Using Multiple Representations to Teach

Composition of Functions." Mathematics Teacher 106, no. 4 (2012): 260-268.

Contains a sorting activity to strengthen concept, definition of function

Wilson, Frank C., Scott Adamson, Trey Cox, and Alan O'Bryan. "Inverse Functions:

What Our Teachers Didn't Tell Us." Mathematics Teacher 104, no. 7 (2011): 500-

507. Uses context to teach inverses; therefore, solve for the independent variable.

Appendix C - Activity Worksheets