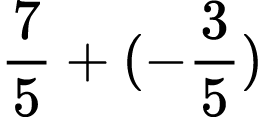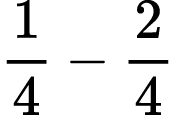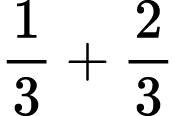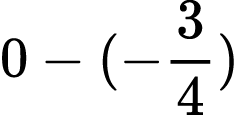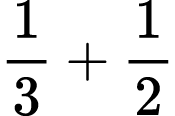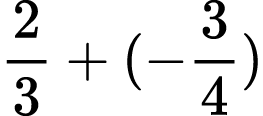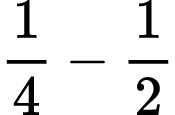“…in the end, the rules are a poor substitute for sense-making.”¹

Introduction

I am a strong believer in The Opportunity Myth. Research has shown that when students are denied access to grade-level work, racial inequities are made worse and students fall even further behind.² All students deserve rigorous, grade-level instruction. And they deserve a teacher who unequivocally believes they are capable of being successful. What my students need most right now is to learn how to think critically and to become effective problem solvers. I believe in my students and I love and support them both in and out of the classroom. 

High school students arrive in my classroom lacking number sense and the reasoning skills necessary for success in high school math and science. In a perfect world I would have the time needed to teach my students the conceptual understanding they are lacking. I would also have time to build fluency and practice, practice, practice all the types of problems students should be able to solve by the time they enter high school. Unfortunately, I live in the real world and there is not enough time to fully remediate my students. Without some type of remediation, my students struggle to engage in grade level course work. My priority is to provide the opportunity to every student to learn grade level content. This conundrum leads to the rationale for this unit: this unit will provide a starting point for some targeted acceleration of learning. My hope is that, after completing this unit, each of my students will have increased both their number sense and their ability to reason proportionally.

Student and School Background Information

I teach at Webster High School in Tulsa, Oklahoma. Webster is the largest physical campus and has the smallest enrollment among Tulsa Public Schools (TPS) high schools. Located in West Tulsa, Webster has a rich history as an integral part of this unique community.

There are approximately 400 students enrolled at Webster High School. The student body is culturally diverse. Approximately 33% of students are white, 21% are black, 19% are Hispanic, 12% are multi-race, 11% are Native American, 3% are Hawaiian/Pacific Islander, and 1% are Asian.

All students at Webster receive free and reduced lunch. English Language Learners make up 13% of the school population. Approximately 25% of students are on an IEP but only a small percentage of those students are in Special Education classes. The teacher shortage is exacerbating this situation. Last year we did not have a Special Education direct instruction teacher for math until midway through the school year. This resulted in many students on IEPs being in general education math classes despite their IEP requirement to be in direct instruction math classes with a Special Education teacher. This increased general education class sizes and left general education teachers with the added role of supporting students who are identified as not being successful in general education math classrooms. Webster is also identified as a low performing school within TPS and the State of Oklahoma.

The diversity of Webster is reflected in each of my classes. Well over half of my students are chronically absent and have moved from school to school throughout their academic careers. The pandemic has exacerbated the challenges of teaching these students. Students are missing many foundational math skills, they are lacking in number sense and fluency, and most students lack the productive disposition which is necessary for students to learn mathematics successfully.

My challenge is to create multi-tier scaffolds so that all students can enter the curriculum. I also must dedicate time to building number sense and to teaching concepts which should be prior knowledge. Most importantly, I must help students believe they can do the work required and that the work is worth their effort.

This unit will be a “Unit 0” for my Geometry classes. My goal is to create a unit which will strengthen number sense and leave students with improved proportional reasoning skills. I believe that if I do this well, the unit could be used in Algebra I and with slight modifications used in middle school math classes as well.

Content Objectives

As students enter high school, there is an assumption that they have developed the ability and maturity for proportional reasoning.³ In reality, when students enter high school, over 90% do not reason well enough to learn high school mathematics and science with understanding.⁴ Most of the students I teach are not capable of proportional reasoning on the level needed to succeed in high school math and science. A great number of my students also enter high school lacking number sense. By number sense I am referring to the set of skills which we use to work confidently and efficiently with numbers; the skills needed to work with multiple operations in one context; the ability to apply numbers in real world situations. This lack of number sense interferes with students’ ability to become strong proportional reasoners as well as their ability to succeed in higher-level math.

In elementary grades students often fail to tie mathematical concepts together. For example, many students think each number system (natural, whole, integers, rational) is a separate math concept to learn about with its own rules and algorithms.⁵ This “silo-ing” makes students believe that each set of numbers has different rules. The consequence is that a student who confidently manipulates and manages integers believes they know nothing about manipulating fractions. My students need to realize only one number system exists and the same Rules of Arithmetic (see Resources) apply to fractions much as they do to integers. They need a clear understanding of number relationships. Is -5 > 3 or is -5 < 3? Is ²⁄₃ = ¹⁰⁄₁₅? Does ³⁄₅ lie to the left or the right of ¹⁄₂ on the number line? This number sense is needed for students to improve their proportional reasoning skills. My unit will engage students in work which will reduce misconceptions and increase student understanding of number relationships.

Using the Number Line to Increase Number Sense

In Roger Howe’s Transitions in the Conception of Number: From Whole Numbers to Rational Numbers to Algebra seminar, I have discovered that the number line is the perfect tool to center student understanding of number relationships and operations. By spending time at the beginning of the year tying what we know about numbers to the number line, we will be able to associate future class work with the number line and build on the foundational concepts we explore in this unit.

Before students can understand operations and how numbers relate to each other, they must understand what a number line is. The number line is a measurement tool. Each number represents a set distance from zero based upon the unit of measure. A point is identified as zero. This point is referred to as the “origin”. The length of 1 unit is chosen. The number 1 is placed the chosen distance from zero. The rest of the points are then placed as multiples of the distance from zero to 1. Positive numbers are placed to the right of zero. Negative numbers are placed to the left of zero and are a reflection across the origin of the positive numbers. Student conceptual understanding of addition, subtraction, multiplication, and division, rests on a clear understanding that the numbers on a number line represent distance.

Figure 1: Numbers on a number line are placed the same distance apart.

Numbers on a number line also represent direction from the origin, or orientation. Using arrows or vectors to show direction provides a visual reference. For high school students who lack a clear understanding of number lines, the arrows should provide a powerful visual which demonstrates both distance and direction. Arrows also provide a necessary tool for understanding why and how addition and subtraction work.

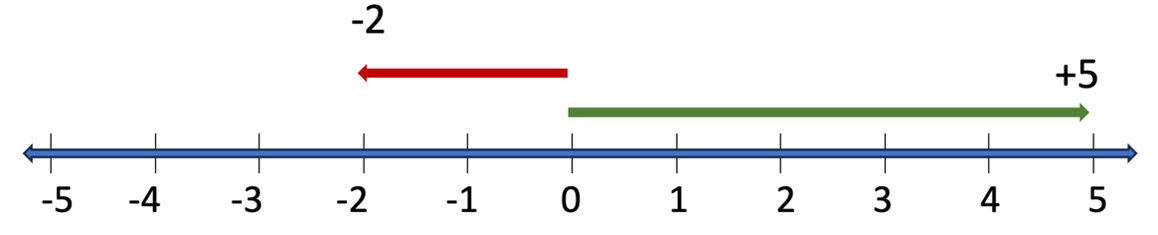
Figure 2: Arrows are used to show that each number on a number line has both distance and direction.

Many students fail to understand how numbers compare to each other. Placing a wide variety of numbers on the number line allows us to see how numbers are greater than or less than each other. It also builds an understanding of equivalent fractions. I believe this understanding is necessary for students to make sense of ratios. If ratios do not make sense to a student, then the student will not be able to reason proportionally. For example, to successfully recognize two geometric figures are similar, a student must recognize that the ratios of corresponding sides are equivalent fractions. See Figure 3.

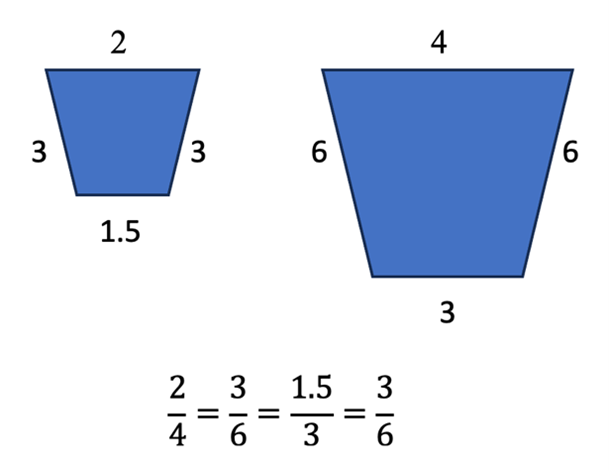
Figure 3: The ratios of corresponding sides of similar figures are equivalent fractions.

Figure 4 shows the fractions between 0 and 1 with denominators of 1, 2, 3, 4, and 5. Even with this small sampling, the equivalent values of different fractions become evident.

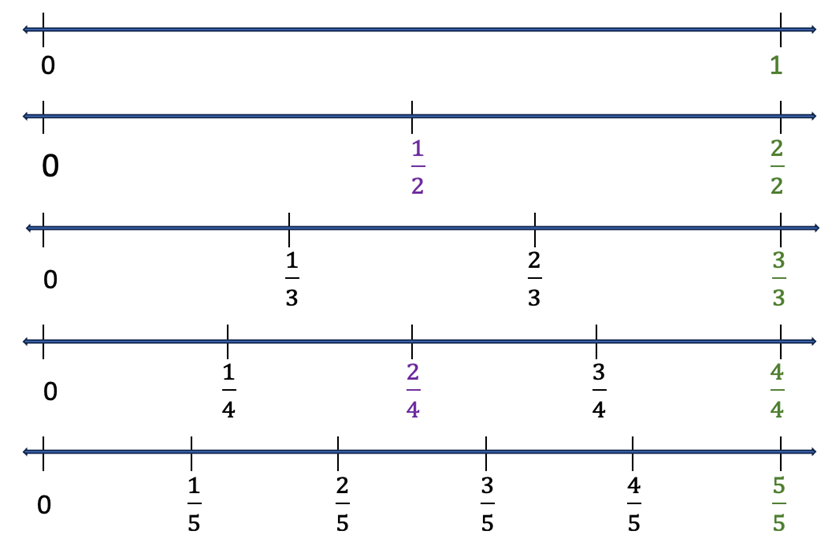
Figure 4: Fractions on numbers lines with denominators of 1 through 5.

Continuing this work to include denominators of 6, 8, and 10, the opportunity for comparison increases dramatically. Below are pictured the interval between 3 and 4, with the locations of these fractions. We see more equivalent numbers. We can compare fractions with a denominator of 10 to decimals of the same value. We can even estimate where  falls on the number line. (Visualizing π as a number is an added value of number line work. Most of my students lack any substantive understanding of what  is. When asked, they respond “3.14”, but are unable to explain that  is the ratio of the circumference to the diameter of a circle. The idea that π is a number seems to elude them. Seeing where π falls on the number line as part of a discussion of what numbers are and how they compare to each other will help students to deepen their understanding of π.)

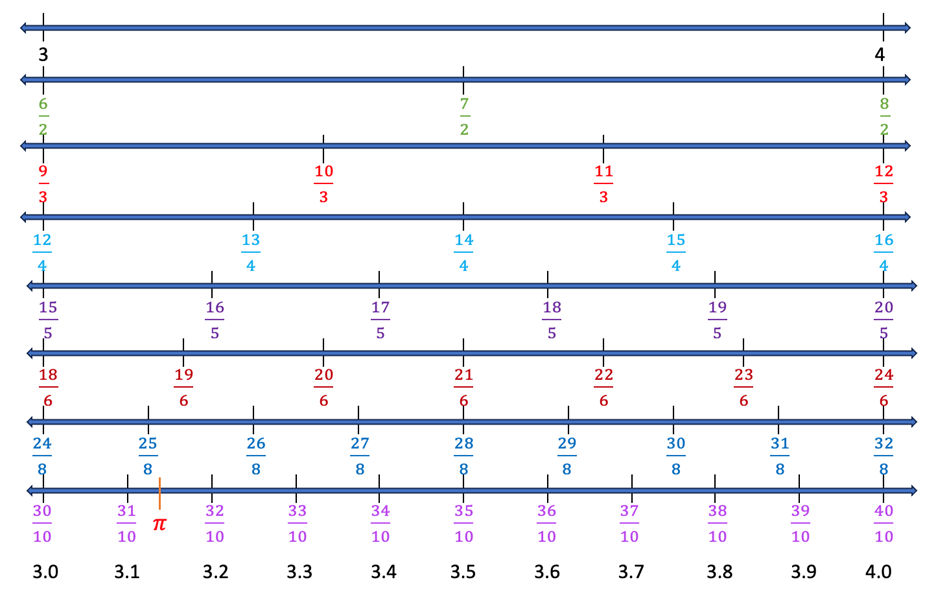
Figure 5: Comparing fractions between 3 and 4.

In Figure 5, notice:

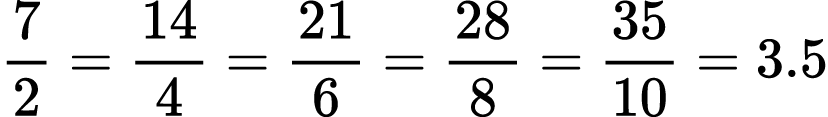
What other equivalent number relationships become apparent when you examine Figure 5?

Simply working with a number line to place various whole numbers and fractions will improve student number sense and should improve student ability to compare fractions. The most important learning with respect to becoming strong proportional reasoners is found when a student develops a solid sense of equivalent fractions and comes to understand that for two fractions to be equivalent, they should express the same ratio or relative size.⁶

As students become proficient with fraction placement on the number line, it is helpful to ask them to compare fractions. On the number line in Figure 6, where would you place ³⁄₅? What about ¹⁄₃? Is ³⁄₅ less than or greater than ¹⁄₂? How do you know? Is ¹⁄₃ less than or greater than ³⁄₅? How did you think about that question?

Comparing fractions should lead some students to discover how the numerator and denominator influence the size of the fraction. As a teacher, I need to make sure that all students understand that when a denominator is fixed and the numerator of a fraction gets larger, the fraction gets larger. In Figure 4, notice ¹⁄₄ < ²⁄₄ < ³⁄₄. But when a numerator is fixed and the denominator of a fraction increases, the fraction becomes smaller. In Figure 4, notice ¹⁄₂ > ¹⁄₃ > ¹⁄₄ > ¹⁄₅.

One way to approach this type of problem is to think in terms of what the fractions might represent. A teacher could provide some context to help students analyze the value. For example, they could think in terms of cookies and people. Maybe yesterday I had 3 cookies to share with 5 people, but today I have 1 cookie to share with 3 people. Picturing cookies for people can help some students visualize and conclude that 1 cookie shared 3 ways results in smaller pieces than 3 cookies shared 5 ways.

Looking at Figure 6, you can see another way students might begin answering these questions.

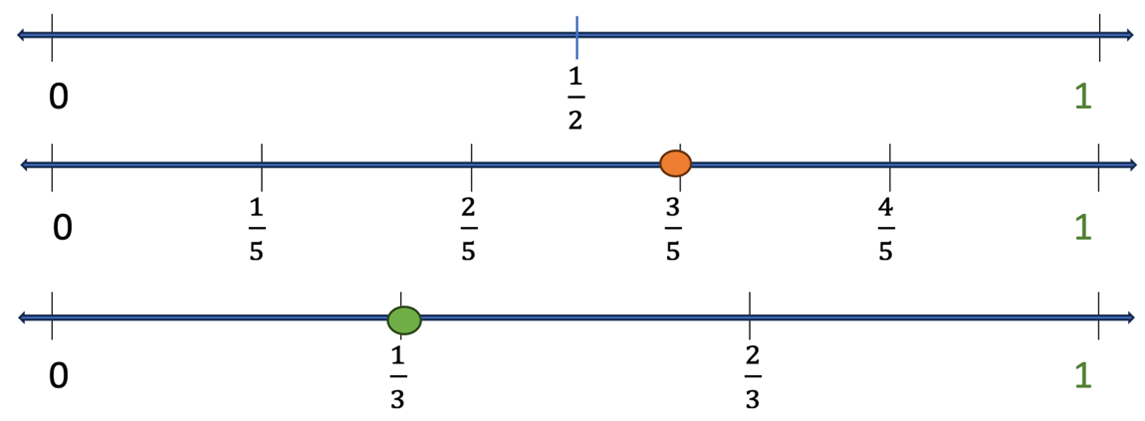
Figure 6: Which is larger? ³⁄₅ or ¹⁄₃?

As students become proficient comparing fractions with lower denominators, I will challenge their understanding by introducing higher denominator fractions. The use of higher denominators pushes students to analyze the problems and look for a more efficient way to solve them. Imagine comparing ⁵⁄₁₂ and ⁴⁄₁₇. Creating the appropriate number lines to compare these two numbers is a much heavier lift than for ¹⁄₅ and ¹⁄₃. Students who understand how the numerator and denominator influence the size of a fraction, will find it easy to apply those principles and see that ⁵⁄₁₂ > ⁴⁄₁₂ > ⁴⁄₁₇. Working through these types of questions will develop student ability to work with equivalent fractions and some students may even discover the property of common denominators before being taught the algorithm.

Most of my high school students are competent at addition with integers. They are often less confident with subtraction. They are unsure about when the result is a negative and when it is positive. During Roger Howe’s Transitions in the Conception of Number: From Whole Numbers to Rational Numbers to Algebra seminar I discovered that the number line is a useful tool to develop conceptual understanding about what is happening when we add and subtract. Using the number line to add and subtract also leads to an understanding that subtraction of a given number is adding the negative of the number. This also gives students an opportunity to apply the Rules of Arithmetic for addition and see the Additive Inverse Property at work. (See Resources) In my experience, students who have conceptual understanding of a math concept, can confidently derive correct responses to questions related to that concept.

Modeling addition and subtraction with a number line is done with directional arrows. Students can visualize not only the absolute value or measure of a number but its direction. My hope is that the clarity provided by the number line as a tool for subtraction is visible and clears up student misconceptions about what happens during subtraction.

Think of the arrow which represents a number on the number line as having a beginning and an end. The beginning is the end that aligns with the origin; the “flat” end of the arrow. The end is the arrow end. Addition is modeled by moving one of the arrows so that its beginning lines up vertically with the end of the corresponding number. Addition of two positive numbers is illustrated in Figure 7a. Notice that the arrows line up like train compartments, end to end. Addition of a positive and a negative number is illustrated in Figure 7b. The arrows representing a positive and a negative number are oriented in opposite directions. You could lay the end of one arrow on the beginning of another, but it is easier to see what is happening when you stack the arrows on top of each other.

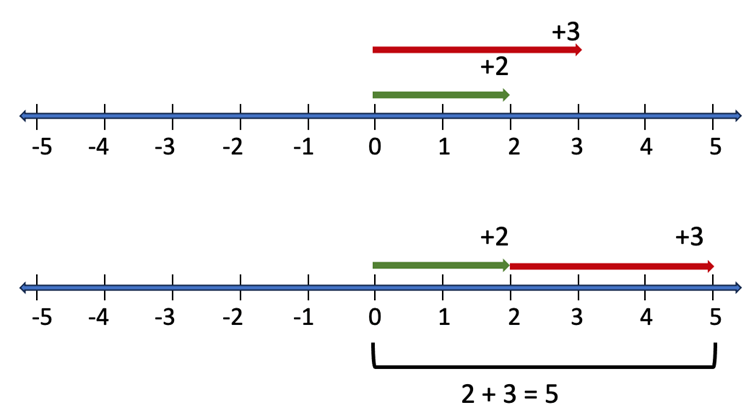
Figure 7a: Addition of 2 positive numbers.

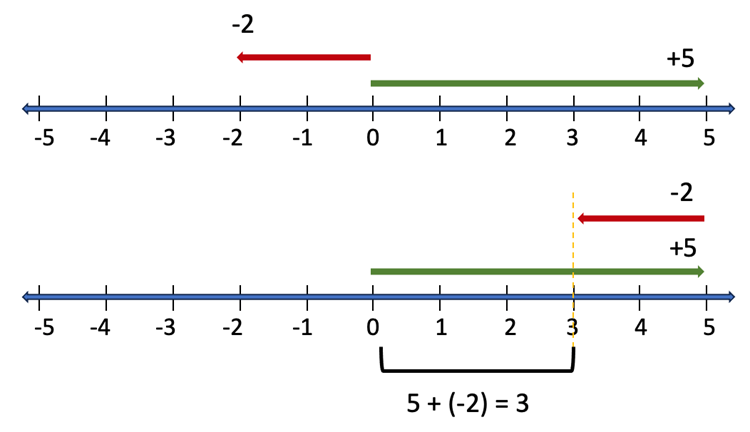
Figure 7b: Addition of a positive and a negative number.

Most of my high school students realize that subtraction is the opposite of addition. Once a student understands that numbers correspond to directed lengths, it becomes clear that on the number line, the opposite of moving to the left is moving to the right. In Figure 7c we see that subtracting  is accomplished by changing the direction of the  arrow so that it points to the right. The visual context supports student understanding of the operation of subtraction and additionally answers the question why a negative of a negative is a positive.

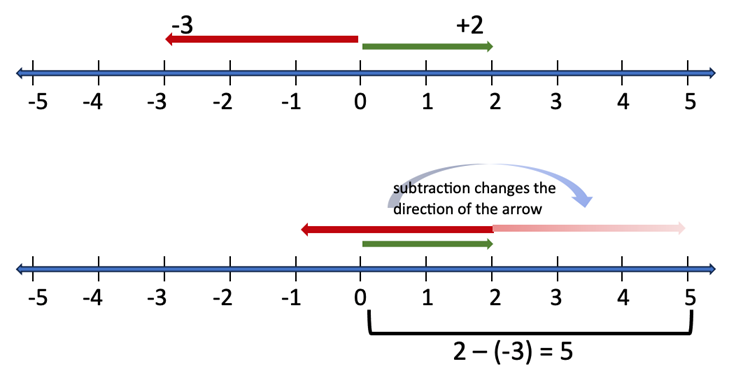
Figure 7c: Subtraction modeled on the number line.

The number line allows students to see the operations are the same operations that are used with integers. A connection can be made between integers and fractions as numbers to which the Rules of Arithmetic apply in the same manner. (See Resources) I am optimistic that the layer of mystery that surrounds fractions for so many of my high school students can be eliminated with the number line model. Figures 8 demonstrates addition of fractions which have the same denominator.

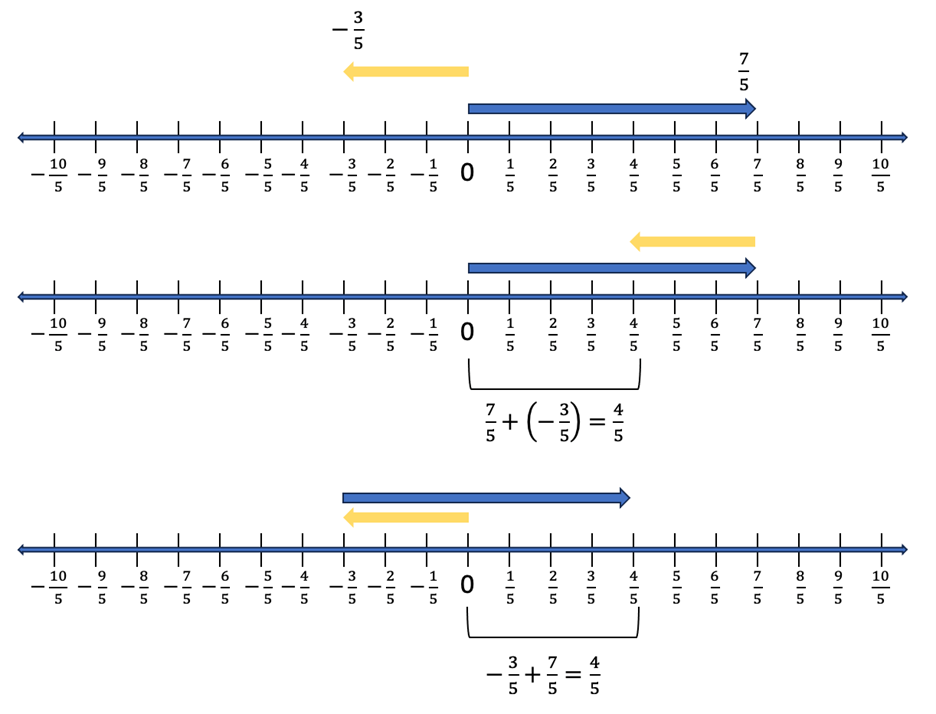
Figure 8: Adding fractions with the same denominator.

The work I did during Roger Howe’s Transitions in the Conception of Number: From Whole Numbers to Rational Numbers to Algebra seminar leads me to believe the most important use of the number line, with respect to building proportional reasoning, is the addition and subtraction of fractions with different denominators. Students can discover the need for common denominators. An understanding of equivalent fractions is required, and students must be able to partition the number line correctly. Adding ¹⁄₃ and ¹⁄₂ requires students to recognize that simply putting arrows on the number line is no longer enough. To find the answer a student must realize that it will take 6 partitions (the common denominator of ¹⁄₃ and ¹⁄₂ is 6) to identify the answer on the number line. See Figure 9.

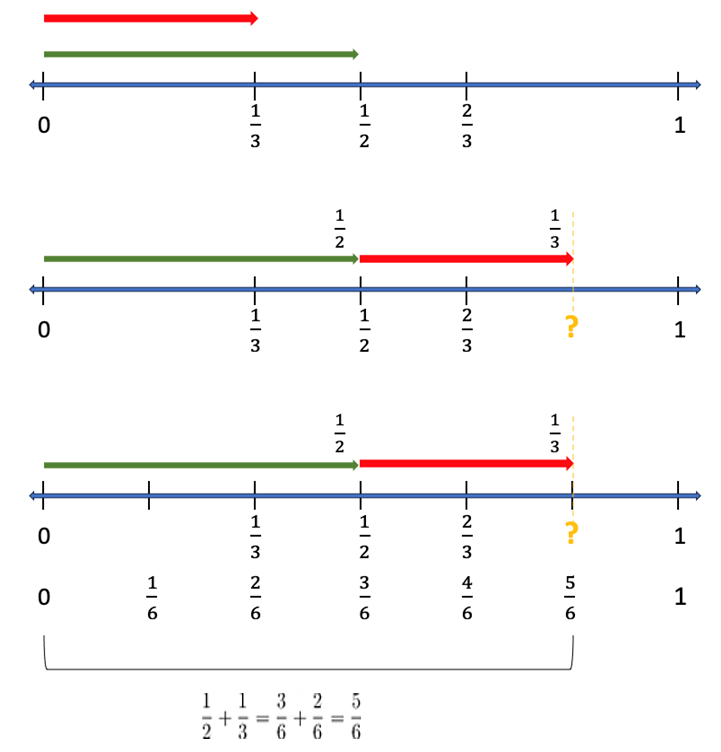
Figure 9: Discovering common denominators by adding fraction on the number line.

The number line provides students with the opportunity to develop many skills. For this unit, we will focus on the skills I have mentioned. To improve my students’ number sense and set the stage to dive into proportional reasoning skills, this unit targets the number line work which supports student understanding of comparing numbers and equivalent fractions.

Using Increased Number Sense to Improve Proportional Reasoning

Proportional reasoning is so critical to student success in higher level math and science that in its Curriculum and Evaluation Standards (1989) the National Council of Teachers of Mathematics (NCTM) claims proportional reasoning “is of such great importance that it merits whatever time and effort must be expended to assure its careful development. (p. 82)”⁷ Proportional reasoning is also referred to as the “capstone of elementary school arithmetic.”⁸ (If this is true, most of my students failed that capstone!) Proportional reasoning requires understanding ratios and understanding situations involving related variables. It is essentially the study of linear equations in two variables, with no constant terms.

Through my teaching experience I have come to believe that reasoning cannot be taught. It must be developed. It must be nurtured. It must be given lots of opportunities to flourish. There are many things I can do as a classroom teacher that will stifle reasoning and creative thinking. I believe my students are best served when I encourage creative thinking about mathematics and we celebrate sound logic that leads to a correct solution. (I also want my students to know the algorithms and rules and be able to fluently apply them. But particularly with the emphasis on proportional reasoning this unit will focus on reasoning rather than rules and fluency.)

When I ask students to reason, I am asking them to think logically about a problem. I am asking them to articulate the “why?” I am asking them to “defend their position.” On a good day, there are as many logical explanations for how to solve a problem as there are students in my classroom.

Proportional reasoning implies the ability to explain a situation which involves the use of proportions. To demonstrate proportional reasoning, students must master a combination of mathematical concepts. Students must be able to work comfortably with multiple concepts at the same time. They must demonstrate fluency and the ability to work with a variety of problem types. To effectively improve student proportional reasoning skills, a broad variety of problem types must be offered so that operations and their algorithms arise naturally as students develop a deep understanding and fraction sense.⁹

The Relationship between Fractions and Ratios

Proportional reasoners understand the relationship between fractions and ratios.¹⁰ A fraction is a ratio between quantities of the same kind. For example,  of the pizza is one slice of one pizza which has been cut into 8 equal pieces. A ratio describes the size of two quantities relative to each other. For example, the ratio of boys to girls in a class. See Figure 10. A fraction can be a ratio and a ratio can usually be expressed as a fraction. (Note that a rate is a ratio that allows conversion between quantities measured in different units. The inclusion of rates is implied in the discussion of ratios.)

In figure 10 a classic example of fractions and ratios is illustrated with a class of 7 boys and 4 girls. Girls are ⁴⁄₁₁ of the class. Boys are ⁷⁄₁₁. Each fraction represents the part (girls or boys) compared to the whole (the total number of girls and boys in the class). The ratio of girls to boys is 4:7 which can also be written ⁴⁄₇. The ratio of boys to girls is 7:4 or ⁷⁄₄. Each ratio represents a comparison of the two parts (boys to girls or girls to boys) that make up the class.

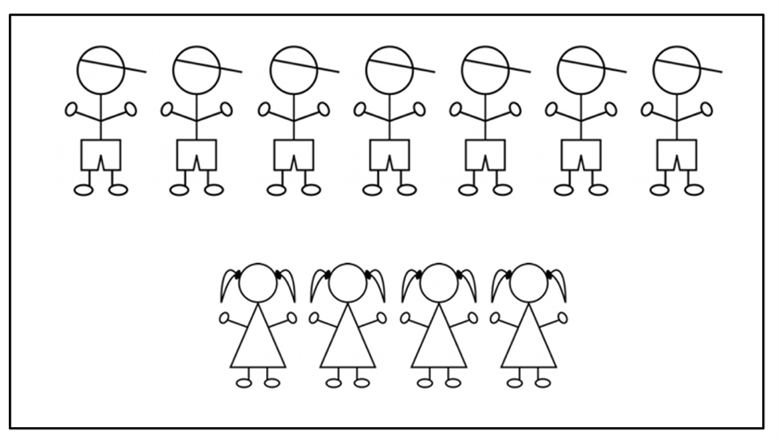
Figure 10: Comparing the number of girls and boys in a class is an often-used example to compare fractions to ratios.

Our work with number lines establishes the general understanding that students need to make the connection between fractions and ratios. Problems involving proportions are often ratio problems. For example, in Geometry we encounter ratios in the Triangle Proportionality Theorem, when we compare corresponding sides of similar polygons, and ratios are also embedded in many other geometric concepts.

What Is the Unit?

In my experience, there can be no proportional reasoning without a solid understanding of fractions. It is not possible to overemphasize the change in student thinking that must occur as students are introduced to fractions. Before any work can be done with a fraction, a student must know what the unit is. It is not possible to identify a fraction until you answer the question “What is the unit?” How are we measuring the whole which we will compare the given quantity to?

There is no rule or algorithm that can be used to identify the unit in a fraction problem. Fraction problems are greatly varied, and different students tend to struggle with different types of problems. In Teaching Fractions, Susan Lamon identifies six types of fraction problems and asserts that to develop proportional reasoning students need lots of experiences with each type of problem.¹¹ These problem types are (1) continuous items such as a pie or a cake; (2) more than one continuous item such as 6 cookies or 3 pizzas; (3) one or more continuous items that are partitioned in some way such as a chocolate bar; (4) discrete objects such as marbles or Skittles; (5) discrete objects that usually come packaged in a specific way such as eggs; and (6) composite units such as a pack of gum.¹²

A single item continuous problem might look like this: If Lisa eats one piece of a cake that is cut into 8 equal pieces, what fraction of the cake is left? There is ⁷⁄₈ of the cake remaining.

A multiple item continuous problem might look like this: The baseball team went out for pizza with the coach. There were 10 players and 1 coach. They ordered 5 pizzas which were each cut into 8 equal slices. If every person ate 3 pieces of pizza, what fraction of all the pizza did they eat? In this question “all the pizza” indicates we should consider the order of 5 pizzas as 1 unit. The players and their coach ate a total of 33 pieces out of a possible 40 pieces. They ate ³³⁄₄₀ of the pizza.

One or more continuous items that are partitioned in some way might look like this: Roger has one chocolate bar which is scored so that it is easily broken into 5 equal pieces. He is eating lunch with 2 students. He gives each of these students 1 piece of his chocolate bar. What fraction of the chocolate bar does he have left? Roger has ³⁄₅ of the chocolate bar left.

Discrete objects might look like this: Val has a bag of marbles. There are 3 red marbles, 7 green marbles, 6 blue marbles, and 4 yellow marbles. She shares the marbles with Krissy who only likes green marbles. If Val gives Krissy all of her green marbles, what fraction of the marbles did she keep? There are a total of 20 marbles. Val gives away 7 green marbles and keeps the 13 remaining marbles. Val keeps ¹³⁄₂₀ of her marbles.

Composite units might look like this: Jessica has a package of gum with 10 pieces in it. She shares the gum with her friends Irene, Ulisses, and Irena. If she gives each friend 1 piece of gum, what fraction of the gum has she given away. Jessica gave away ³⁄₁₀ of the package of gum.

Reasoning Up and Down

Students who master the mental process of reasoning up and down tend to develop strong proportional reasoning skills.¹³ Reasoning up and down is a process used when units are clearly defined. It is a way to reason up from a given fraction to a unit fraction, then down from the unit fraction to another fraction. Reasoning up and down is used to move from a starting fraction to the final answer. See Figure 11. It is a mental process and not an algorithm. Each problem must be analyzed on its own. In my experience, as with most mental processes, the more a student practices, the more efficient they will become.

Figure 11: Reasoning up and down.

Students must also be able to reason up and down when exploring problems involving two ratios.

These types of problems are situations which have a proportional relationship between two quantities that are linked together and that vary together. The earlier work in this unit with the number line and equivalent fractions will lay the groundwork for developing student skill at reasoning up and down.

Units and Unitizing

The process of mentally creating groups out of a given quantity is called unitizing. It is a natural process. We all do it without thinking about it. Students are sure to have some level of skill at unitizing. Through my teaching experience, I have come to believe that the ability to unitize is usually an indicator that a student has good proportional reasoning skills.

If I tell you I have 24 cans of Dr. Pepper, how do you think about the cans? Do you think about 24 individual cans (24 units)? Or do you think about four 6-packs (4 units)? Or maybe two 12-packs (2 units)? Or perhaps one large case containing 24 cans (1 unit)? In each instance the number of units is different, and each is a different way to unitize the 24 cans.

The ability to unitize provides students with flexibility and efficiency in solving proportion problems. By thinking in terms of composite units, students can analyze a problem and use the unit that makes the most sense for that specific problem.

Teaching Strategies

Big Picture

In my classroom I use the question “Why?” and challenge students to “defend your position” throughout each class period. Reasoning is “the process of thinking about something in a logical way in order to form a conclusion or judgment.”¹⁴ Proportional reasoning entails analyzing problems which include proportions in a logical manner and forming a conclusion. Students are required to explain their thinking and demonstrate to their classmates and to me that their problem solving is logical.

If my students have learned but not mastered content from previous grades, then in theory I should be able to scaffold with a review. This should “jog” student memories. The reality is that this approach at scaffolding is not effective because multi-year conceptual understanding has not been developed in earlier grades.¹⁵ There is no memory to "jog”. Without conceptual understanding students know a random assortment of rules and do not know when or why to apply them. For this reason, my unit has a primary goal of developing conceptual understanding. Procedural fluency will be a secondary concern and will come with time as we revisit these concepts throughout the year.

Use of “Thinking Tasks”

“If we want our students to think, we need to give them something to think about—something that will not only require thinking but will also encourage thinking.”¹⁶ My goal when introducing any new concept is to get students to engage in problem solving. In my classroom, problem solving is not applying an algorithm. It is not following a rule. It is not looking at an example and doing your best to apply that example to a new question. Problem solving is what we do when we do not know what to do. It is messy. It usually does not follow a linear or efficient path. Students can get stuck. And they can apply their existing knowledge in creative ways to get unstuck.

If a math task is carefully curated and you have a little bit of luck, students will engage and think. When I curate a thinking task for my classroom, I consider what I want students to discover, what misconceptions I expect them to bring to the task, what prompting questions I can ask if students get “stuck”, and how to release the task to students. My goal is a task which allows every student to participate, a task which challenges the most advanced student, and a task with more than one way to reach a solution. I want students to trudge through the messiness. I want them to have ah-ha moments. I want them to have moments when the ah-ha light bulb flickers off as they realize they are off track. I want them to try and fail. Sometime students will give up, so I want a task that is intriguing enough that students will return. And during the most effective and joyful class periods, I want students to argue about and learn all the math!

I first considered the difference between a general problem or math task and what Peter Liljedahl calls “thinking tasks” when I read Building Thinking Classrooms for Mathematics (BTC) a couple of years ago. BTC helped me realize that when I had a red-letter teaching day, it was the result of thinking tasks. Sometimes tasks that I thought would be great, were ho-hum. Other days the task I had chosen or developed was a huge success. Those successes were always the result of what Liljedahl would identify as a thinking task.

To decide whether a task qualifies as a thinking task, I look to what the problem does. I want it to make students think. The task should require students to draw upon a wide range of mathematical knowledge and to put this knowledge together in different ways. If students can discover a new algorithm or mathematical truth that is added value.

In this unit I will plan to at least two thinking tasks. I discuss the implementation of a thinking task in more detail in the Activities section. Each time the task will give students an opportunity to dive deep into a proportion problem. The goal with this unit is for these tasks to stretch student knowledge and to bring together a group of concepts that students want to “silo”. I want to force students to dig into their mathematical toolbox, go outside their comfort zone, and use some of the tools they avoid when the problems are simpler.

Collaborative Groups

Most of my instruction is through activities in which students can work together to solve problems and discover patterns and rules. Students sit at desks arranged in groups of 3 or 4. Almost all work done in my class is collaborative in nature. Students are encouraged to seek help from peers.

Problem analysis is well suited to group discussion. I regularly assign what I call collaborative group work. These are problem sets or thinking tasks with an expectation that students will work with their assigned group during the allotted class time. Collaborative group work is done at the white boards around the room. Standing up increases student engagement and somehow it minimizes cell phone issues. It also seems to make students feel more visible, which motivates them to engage more actively than when sitting at desks. Class norms include one marker per group. If you are talking, you are not writing. The marker is rotated on a regular basis, so every voice is heard and everyone has the responsibility of careful listening and recording their group’s thoughts.

The benefit of collaborative group work is clear and the research supports what I see in my classroom.¹⁷ My favorite part of collaborative group work is when I notice students stepping back from their section of whiteboard to look around the room. Sometimes this is an indication that the group is “stuck”. Students have learned to look for inspiration by looking at their classmate’s work. To find that inspiration the students must be thinking and analyzing work by other students. I love seeing the engagement and desire to understand. Of course, sometimes this move means the group is feeling confident in their solution and want to check out the “competition.”

Notice / Wonder / Discover

Many teachers at all grade levels use the Notice and Wonder protocol to encourage student thinking and noticing. (If you are not familiar with Notice and Wonder in the math classroom, I encourage you to check out the resources and research on the NCTM website related to Notice and Wonder.) I have built upon the Notice and Wonder model and added “Discover”. This has become one of my favorite teaching strategies. The goal of this unit is to further student proportional reasoning. This unit is remedial in nature. Students will enter my classroom with varying degrees of number sense and different levels of proportional reasoning skill. I expect that some students who bring more prior knowledge with them will draw conclusions and make connections as we work through the unit. And I expect that other students may engage in the activities and not see any connections on their own, but will learn from their peers, or from the whole class discussion.

During the school year, at key points during each unit, I allot a significant portion of class time for Notice / Wonder / Discover. Students learn the routine. Notes are out. Students usually choose to have an individual whiteboard to work on as needed. I have collected student work that demonstrates common misconceptions. I also have a collection of student work solving the same problem in more efficient and less efficient ways. Sometimes I use work I create if I want to make a specific point that is not visible in student work. Day by day we have shared our thinking and work with each other, so the point of Notice / Wonder / Discover is not so much new discoveries. The point is to bring together related ideas and concepts so we can see the big picture. The goal is for students to make observations about very carefully chosen work samples; to ask questions about those work samples; and then to discuss together with my guidance what we have learned.

When I make the time to carefully choose sample work and I have a clear goal of what I want students to discover, this is always a successful teaching strategy. Most of my students will make the connections, clear up misconceptions, and walk away with a sense of understanding.

Classroom Activities

My curriculum unit will focus on helping students improve their proportional reasoning thereby laying the groundwork for more successful high school math and science experiences. The unit can be used as a “Unit 0” to start the year in any high school math class. Since it is for high school, it will assume elementary understanding of number lines and fractions and work toward bringing the pieces of previous knowledge students bring with them into a cohesive whole.

The Number Line

The unit will begin by defining the number line. I anticipate that many of my students will not need any scaffolding or additional instruction on the number line, but I will plan for supplemental activities/instruction to be used as needed to ensure that all students begin with a solid understanding of number line basics.

Activity 1 (2 Days)

I will begin with instruction that defines number line and related terms. I will emphasize that numbers represented on the number line represent both distance and direction. My goal is for students to understand that the whole numbers 1 and -1 are exactly one unit from the origin (zero). Each whole number is placed a distance from zero that is a multiple of the established unit. After students understand the definition of the number line, each student will use a straight edge and a blank piece of paper to create a number line with numbers from -3 to 3.

As students work, I will move through the room asking individual students questions as needed. Once all students have completed their number line, I will ask whole class questions with the goal of guiding the students to improve their understanding of values of numbers, fraction placement, and fraction comparison. The discussion will guide which questions I ask. Possible questions include:

• Is positive 2 greater than or less than negative 3? How do you know?
• How does negative 1 compare to 0?
• How many units from 0 is negative 2? Positive 3? Positive 1? Negative 3? What do you notice about your answers?
• Where would you place ¹⁄₂? How did you know where to place it?
• Where would you place ¹⁄₄? ¹⁄₈? ¹⁄₁₆?
• Where would you place ¹⁄₃? ²⁄₃? ³⁄₃? ⁴⁄₃? ⁵⁄₃? ⁶⁄₃?

Once students have built a number line and placed an assortment of fractions on the number line, students will work in pairs to add fraction sets to 8 different number lines. Each pair of students will be given a set of number lines to work with. See Figures 12a and 12b. Students will work together to mark each number line from 3 to 4 with all the fractions which have denominators of 2, 3, 4, 5, 6, 8, and 10.

Figure 12a: Side 1 of Activity 1 Student Handout. This handout should be printed on 11x17 paper.

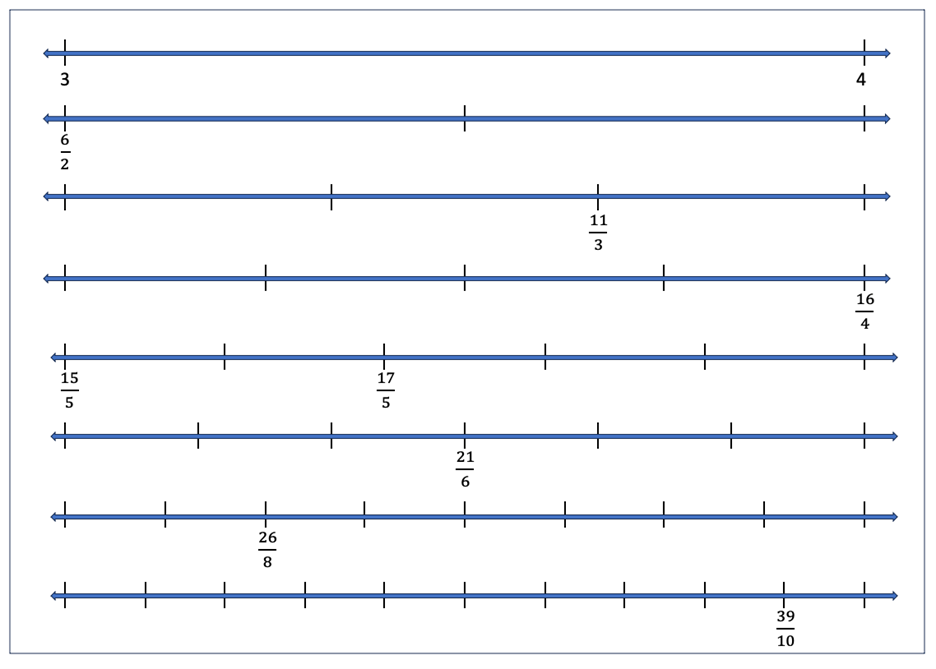
Figure 12b: Side 2 of Activity 1 Student Handout

Again, while students work, I will move through the room asking student pairs questions as needed. Once most pairs have completed their number line, I will ask whole class questions with the goal of guiding the students to improve their understanding of values of numbers, fraction placement, and fraction comparison. The discussion will guide which questions I ask. Possible questions include:

• Is ²²⁄₆ less than or greater than ²⁰⁄₆? How do you know?
• Is ³⁄₇ less than or greater than ⁵⁄₇? How do you know?
• Is ¹⁸⁄₅ less than or greater than ⁷⁄₂? How do you know?
• Is ³⁄₅ less than or greater than ¹⁄₂? How do you know?
• Is ⁷⁄₂ less than or greater than ²¹⁄₆? How do you know?
• What other fractions are equivalent to ⁷⁄₂?
• What is another fraction equivalent to ⁷⁄₂ that is not on our paper? How did you think about that? What is a different way to think about that?
• Is ¹⁰⁄₃ less than or greater than ¹⁸⁄₅? How do you know?
• Is ¹⁄₃less than or greater than ³⁄₅? How do you know?
• What if you didn’t have these number lines to look at? How would you compare ⁵⁄₁₂ and ⁴⁄₁₇?

What I want my students to demonstrate at the end of this activity is a clear understanding of the magnitude of positive and negative numbers. Do my students understand that it is the placement on the number line that determines which number in a pair has greater numerical value. Is it clear that distance from zero is one concept and relative value is a different concept? Do my students recognize equivalent fractions? Do my students understand the impact the size of the denominator and the numerator have on the size of a fraction?

Activity 2 (1 day)

With our newly improved number sense because of our recent number line work, we will explore addition and subtraction using the number line. Students will be given a handout with 10 number lines numbered from -5 to 5 on one side of their handout and 10 number lines numbered 0 to 1 including various fractions represented on the other side. We will begin by recalling how arrows represent the distance and direction of numbers on the number line.

The initial work will be done whole class guided by slides. See Figure 7a for an example. The first slide would show the first number line in Figure 7a. It would be followed by a slide showing the second number line in Figure 7a. I anticipate it will take 5 to 8 problems for all students to be comfortable representing whole number addition and subtraction on the number line. In each class, I will present as many problems as needed before moving on to working with fractions.

Possible expressions I could ask students to represent/solve include:

• -3 + 2
• 1 + 4
• 4 + 1
• 0 + 3
• 5 + (-2)
• (-2) + 5
• (-2) + (-3)
• 2 - (-3)
• (-3) - 2
• 1 - (-4)

As we move to adding and subtracting fractions, I will start with common denominators and then move to expressions with different denominators. Students will need to think about the fractions and mark their number lines accordingly if the needed partitions are not represented. Several 0 to 1 number lines with no fractions will be provided giving students different options for how they approach solving these expressions. The primary goal of working with fractions in this context is for my students to deepen their conceptual understanding of equivalent fractions.

Possible expressions I could ask students to represent/solve include:

Proportional Reasoning

Once we have completed our number line work, I will introduce proportional reasoning with a thinking task. Students will be randomly assigned to groups of 3. Students will stand with their group and gather around a rolling whiteboard in the center of the room. I will introduce the following problem which is adapted from Teaching Fractions.¹⁸

Activity 3 (1 day)

Problem: There are two large pitchers which contain tropical punch flavored Kool-Aid. Each pitcher of Kool-Aid has been made by mixing powdered Kool-Aid flavoring with water. The powdered Kool-Aid comes with a standard size scoop. One pitcher is made with 4 scoops of Kool-Aid mix and 2 gallons of water. The other pitcher is made with 4 scoops of mix and 3 gallons of water. Students are asked to compare the Kool-Aid in the two pitchers.

Questions include: Will one of the drinks have a stronger tropical punch taste? How could you measure the “punchiness” of any Kool-Aid mixture made with the powdered Kool-Aid flavoring and water? Does it matter that one of the pitchers has more liquid in it than the other one does? Why or why not? Suppose you obtained 3 measures from 3 different pitchers whose powdered mix to water ratio were 3 scoops of powdered Kool-Aid to 4 gallons of water, 3 scoops to 5 gallons, and 3 scoops to 2 gallons. How would you use these numbers to rank the mixtures from the weakest to strongest tropical punch taste?

I present the entire problem stopping to draw pictures of the pitchers to provide students with a visual. I will write each question on the board as well. I will ask a student to sum up the facts as a check that students understand the general problem. Then the students are sent to find a space at the whiteboards around the classroom to work on the problem. I do not answer questions until students have had time to work. And as part of the class norm we establish for this type of task, I will not confirm or deny whether students have arrived at a correct answer. I will not directly answer questions about what to do next or how to start. I will answer almost every question a student has by either referring them back to the illustration on the whiteboard that I drew or by asking the student a question to help them move forward.

When I release the students to start working, I task them with answering just the first question. Once a group is confident in their answer to the first question and can explain their “why”, the group will move forward to the more general question of how to measure “punchiness” of any given mixture.

As the groups dive into the problem, I anticipate most students will recognize which pitcher has the strongest taste. By asking how to measure the “punchiness” students will have to think about an answer that is not dependent on the numbers in a specific situation. They will have to generalize what they know about a specific situation. Students will also have to think about what happens to the taste as you add more water or less water.

We will come together as a group to debrief before the end of class.

Activity 4 (3 to 4 days)

The remainder of our time in this unit will be working word problem sets. We will work with selected problems and problems adapted from Teaching Fractions. Students will work with their groups. I will move through the room pushing in as needed. At the end of each class we will come together and share our problem solving strategies.

I will use 3 different sets of word problems. The first set will be proportion problems which do not include numbers. I believe the advantage of using word problems without numbers is that it allows students to not be distracted by the urge to get a final answer. So many of my students approach word problems by pulling out all the numbers they see, adding operations, and hoping for the best. This first set of problems will give students a chance to think about what proportions are and to focus on recognizing the units. Example problems of this type can be found in Teaching Fractions.¹⁹

I will supply numbers for the second set of problems. We will begin with 2 or 3 of the problems from the first set to allow students to see the “next step” in solving problems they have already spent time with. Then we will move to a group of problems in two distinct sets. Each set will be similar problems that are each slightly different. The first set of problems will be related to unit conversions. My students struggle with unit conversions. This struggle impacts their success in both math and science. The second set of problems will be related to interest rates. I believe the real-world application of interest rates will help prepare my students for the adult world of credit cards (and what a bad deal they are!) as well as help them to understand car loans and how compound interest works. Ideas for problems of this type can also be found in Teaching Fractions.²⁰

For the final set of problems, I will work with examples of more challenging problems from Teaching Fractions.²¹ The first two problem sets will include 20 problems each. This final set of problems will contain 3 to 5 problems designed to work like our thinking problems. Depending on how students are progressing I may choose one problem and spend a class period working it with our Thinking Tasks protocol. Then I will introduce a set of 3 challenging problems as group work the next day.

Resources

Rules of Arithmetic²²

1. Commutative Property for Addition: for any two numbers a and b,

a + b = b + a

2. Associative Rule for Addition: for any three numbers a, b, and c,

(a + b) + c = a + (b + c)

3. Existence of Additive Identity (aka Zero): there is a number 0 such that for any number a,

0 + a = a

4. Existence of Additive Inverse (aka “the negative” and “the opposite): for every number a, there is another number, called the additive inverse or negative of a, and denoted by -a, such that

-a + a = 0

5. Commutative Rule for Multiplication: for any two numbers a and b, we have

a X b = b X a

6. Associative Rule for Multiplication: for any three numbers a, b, and c,

(a X b) X c = a X (b X c)

7. Existence of Multiplicative Identity (aka One): there is a number 1 such that for any number a,

1 X a = a

8. Existence of Multiplicative Inverse (aka “the reciprocal”): for every non-zero number a, there is another number, called the multiplicative inverse or reciprocal of a, and written as ¹⁄_a(or sometimes also as a^-1), such that



9. Distributive Rule: for any three numbers a, b, and c,

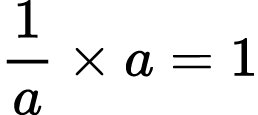
a X (b + c) = a X b + a X c

Annotated Bibliography

"Adding It Up." National Academies Science Engineering Medicine. Accessed April 22, 2023. https://nap.nationalacademies.org/catalog/9822/adding-it-up-helping-children-learn-mathematics. Introduction to how students in pre-K through 8th grade learn mathematics with recommendations for ways to change how we teach math.

Bingea, Aaron. "Adding and Subtracting Rational Numbers on the Number Line." Yale National Initiative. 2016. https://teachers.yale.edu/curriculum/viewer/initiative_16.05.01_u. Exemplar curriculum unit clearly explaining how the use of the number line can be used to help middle school students master fraction addition and subtraction.

Burns, Marilyn. About Teaching Mathematics: A K-8 Resource. Portsmouth: Heinemann. 2022. Seminal resource for all math teachers provides an in-depth overview of the issues surrounding teaching mathematics.

Howe, Roger. n.d. "From Arithmetic to Algebra." Mathematics Bullitin: A journal for educators 13-22. (Chinese math education journal, copy of article provided by Roger Howe). How arithmetic word problems can help students learn algebra.

Howe, Roger, and Solomon Friedberg. "The 'Rule of Signs' in Arithmetic." November 10, 2008. (not published, copy of article provided by Roger Howe). Justification for the Rules of Signs.

Lamon, Susan J. More: In-Depth Discussion of the Reasoning Activities in "Teaching Fractions and Ratios for Understanding". London and New York: Routledge. 2012. Exemplar answers and explanations of problems in Teaching Fractions and Ratios for Understanding.

Lamon, Susan J. Teaching Fractions and Ratios for Understanding: Essential Content Knowledge and Instructional Strategies for Teachers. London and New York: Routledge. 2020.

How students develop an understanding of fractions and ratios with lots of sample problems.

Liljedahl, Peter. Building Thinking Classrooms. Accessed July 15, 2023.  https://buildingthinkingclassrooms.com. Teaching practices that get students to think.

NCTM. Principles to Actions: Ensuring Mathematical Success for All. NCTM. 2014. Research-based teaching practices that should be implemented to ensure that all students are mathematically successful.

Newman, Jamila, and Bailey Cato Czupryk. “Six Practices for Accelerating Student Learning This Year”. 2021. TNTP: Reimagining Teaching. October 25. https://tntp.org/blog/post/6-tips-for-accelerating-student-learning-this-year#:~:text=But%20we%20found%20in%20our,the%20last%20year%3A%20learning%20acceleration. Why acceleration is more succesful than remediation and how to accelerate learning in your classroom.

Rossiter, Jeffrey. "Rational Number Placement on the Number Line." Yale National Seminars. 2016. https://teachers.yale.edu/curriculum/viewer/initiative_16.05.07_u. Exemplar curriculum unit for developing student understanding of rational numbers.

Schoen, Harold L. Teaching Mathematics through Problem Solving: Grades 6-12. NCTM. 2006. How to use problem solving in the secondary math classroom.

The Britannica Dictionary.  https://www.britannica.com/dictionary/reasoning#:~:text=Britannica%20Dictionary%20definition%20of%20REASONING,Could%20you%20explain%20your%20reasoning%3F. Used to define terms.

Appendix on Implementing District Standards

MP.2 Reason abstractly and quantitatively.

Mathematically proficient students make sense of quantities and their relationships in problem situations. They bring two complementary abilities to bear on problems involving quantitative relationships: the ability to decontextualize and the ability to contextualize.

MP.4 Model with mathematics.

Mathematically proficient students can apply the mathematics they know to solve problems arising in everyday life, society, and the workplace.

MP.7 Look for and make use of structure.

Mathematically proficient students look closely to discern a pattern or structure.

6.RP.A Ratios and Proportional Relationships: Understand ratio concepts and use ratio reasoning to solve problems.

6.NS.C. The Number System: Apply and extend previous understandings of numbers to the system of rational numbers.

7.RP.A Ratios and Proportional Relationships: Analyze proportional relationships and use them to solve real-world and mathematical problems.

Notes

¹ Lamon, Teaching Fractions, 17.

² Newman and Czupryk 2021.

³ Lamon, Teaching Fractions, 12.

⁴ Lamon, Teaching Fractions, 234.

⁵ NRC, Adding It Up, 94.

⁶ Lamon, Teaching Fractions, 240.

⁷ Lamon, Teaching Fractions, 12.

⁸ NRC, Adding It Up, 8.

⁹ Lamon, Teaching Fractions, 48.

¹⁰ Lamon, Teaching Fractions, 48.

¹¹ Lamon, Teaching Fractions, 103-104.

¹² Lamon, Teaching Fractions, 103-104.

¹³ Lamon, Teaching Fractions, 18.

¹⁴ The Britannica Dictionary.

¹⁵ NRC, Adding It Up, 8.

¹⁶ Lildejahl.

¹⁷ Lildejahl.

¹⁸ Lamon, Teaching Fractions, 65.

¹⁹ Lamon, Teaching Fractions, 76 et seq.

²⁰ Lamon, Teaching Fractions, 30 et seq.

²¹ Lamon, Teaching Fractions, 243 et seq.

²² Howe and Solomon.