My overall goal is for students to have a solid idea as to how patterns work and fit together on a wallpaper design. This includes learning the four different types of isometry as well as the 7 Frieze Patterns. Students will learn how to create their own wallpaper by identifying how the isometries and Frieze patterns all work together.
I've always been the type of person who is completely honest with myself on my academic strengths and weaknesses. Math was something I always struggled with in school. I was always the student who loved to read novels and was often told to put down the book and get to my math homework. My parents always knew how much I procrastinated getting my math assignments completed every night. In all honesty, once I got past basic Algebra my problems only got worse. I remember right before I started geometry in my sophomore year both my brothers telling me how easy the subject was compared to Algebra. I could not have been more excited to finally have a math class that would not be much work. I could not have been more wrong. The teacher once told me, "Some people get it and some don't." In the end I think the teacher passed me only because no one could have made more of an effort to get extra help than I had those 9 months. Thinking about geometry has always made me feel like a failure.
I grew up in a home where both of my parents were teachers. My life revolved around education and the successes and hardships of the occupation. My two older brothers were the type that did not have to study hard to get good grades and being the youngest I was expected to follow in their foot steps. Teaching is a third career for me and probably the greatest life choice I've ever made yet by far the most difficult job. When deciding what subject to focus on I thought a lot about my failure in geometry and other areas where I had a hard time in school. There was no one who would take the time to offer differentiated instruction and the way it was taught in the book was the way the teacher presented to the class. Everything was taught using two dimensional figures and there was not one hands on activity. I've often thought to myself maybe my experience in geometry would have been much different if I could touch and see these shapes and figures. That could have been the missing piece of the puzzle.
When I decided to become a special education teacher it was reasons such as this that inspired me to work with this population of students. I understood their struggle in those subjects that didn't make sense and how frustrating things can be when you look down at your homework assignment and have no idea where to begin so you just start crying. No matter who the student is or their background, everyone wants to be successful. There is no better feeling than receiving a good grade on something you put a lot of time into completing. A good grade gives such a feeling of accomplishment and that all the effort was well worth it. Failing students just look at it and think, "Why keep going?" and just give up.
My goal as a math teacher is to empower students to want to learn and to take an active role in their education. For anyone who has never been identified with a learning disability it would be difficult to understand how much it effects your education and learning style. While I didn't give up and was motivated to pass I can easily see how anyone would just walk away after making such efforts to do well. I now believe that, if it is taught right, anyone can learn any subject.
Every year my goal is to form a community in my classroom, not just a room that a student sits down, stays quiet and takes notes. That has never been my style. It is important for me to remember that, in special education, most students come to me as reluctant learners, especially in math. In designing my lesson plans around a subject I had a difficult time with at their age, I knew I would have to be not just thorough, but incorporate a good balance of hands on activities, paperwork and lecture time. These students are already very much behind where they should be when they walk through the doors of room 224, so we don't have time to waste. Knowing this I have to design something that has the biggest bang for the dollar, so I cover the most important things.
I have been a special education teacher for 7 years and in that time I have witnessed school administration and other teachers dismiss my students as not being able to achieve the high standards of the general education population. Since I am a very realistic person I know we all have our limits, but if something is taught using a variety of different methods couldn't we at least give geometry a try? All students are required to participate in statewide testing once a year in various subjects and Geometry is one of those subjects, but one that I have never taught. When speaking to other math teachers at my school I have learned most of what is on the state testing is basic Geometry. If the students can pick up some of the basic ideas they will be able to at least answer half the questions. While conducting my research of what I really needed to cover and what can be left aside I decided to look at the state standards, consult a math teacher from my school, Professor Roger Howe and one of the books Professor Howe recommended we read. It was then that I understood grids and how things move on them and measurement of angles as the most basic and elementary idea behind geometry. This is something I was never taught and am now just learning. In my observations I have found students have a natural understanding of symmetry and finding a pattern, but need to be taught the more sophisticated ideas such as transformations, rotation, reflections and translations - all rigid motions that tell them how these shapes move within a grid. Studying symmetry transformations also teaches students to pay attention to both the angle measures and length of sides in order to produce an image that is congruent to the original shape.
Everywhere we look one can find symmetry in the environment around us. According to Marcus du Sautoy "Symmetry…A Journey into the Patterns of Nature", "For the mathematician, the pattern searcher, understanding symmetry is one of the principal themes in the quest to chart the mathematical." 1 It takes a trained eye to understand that symmetry is just not about patterns, but how the shapes and figures on that pattern move within the grid it is built upon. This is a new concept for me because I have never trained myself to understand this idea or even expected that it existed. As a very observant person, I can easily identify shapes and patterns within my own space. I never really thought about how all of it fits together in a mathematical format. Anything with a pattern, no matter what it may look like, has symmetry: from art, architecture and even music we listen to everyday. I personally even believe people have symmetry between each other since our DNA is constructed in symmetric form, but that's not math talk.
So what is symmetry exactly? Well from my understanding, symmetry is a shape or image that is repeated to create a balanced pattern. In other words it's not just a bunch of random shapes and images that are unrelated then placed upon a grid. No, there is a balance to it that is determined by what type of symmetry is being used. Symmetry is produced by transformations. The mathematical language is: a figure (or design or pattern) is symmetric under a transformation, if it is left unchanged by doing that transformation. The collection of all transformations that preserve a figure is its collection (or group) of symmetries.
The most familiar transformations are isometries. These can be broken down into four different types: reflection, rotation, translation and glide reflection. Each type of symmetry can be identified based on procedures for testing, but before anyone can test for the type of symmetry you need to have a good understanding as to the characteristics of each type. Remember while there are four different types of isometry, it is not only important to understand how they work on a grid, but it is also essential to comprehend how all four interact with each other because there are mathematical rules to everything.
When I hear "reflection" symmetry I automatically think about mirrors which are exactly what it is all about. So what exactly does a mirror do? Well in its most basic definition a mirror is a piece of glass that reflects light so that when looking into it one can see themselves in it. So how is that important in math? Honestly, it's not so easy to explain, but there is a reason for it. First I must lay out what a reflection or mirror symmetry looks like. Remember making hearts for Valentine's Day cards? Fold the paper in half and cut a half shape of a heart along the folded side. Open it up and you have a heart shape. That is reflection/mirror symmetry. Not that the heart itself has anything to do with symmetry and geometry, but it was created through another image; the half heart, using reflection. Reflection across a line (called the axis of reflection) is a transformation that takes any given point to the point opposite to it on the other side of the line – at the same distance, and on the perpendicular from the original point to the line. Each half heart is the reflection of the other across the midline of the heart. It is an important concept for geometry because it is an isometry, one of the "Legal Move"s, which are motions that can be symmetries of wallpaper/patterns. 2
If a figure has reflection symmetry across a line, every pair of mirror image points on the mirror are unchanged by the reflection, resulting in the image being exactly the same on both sides. A shape and its mirror image are both the exact same distance from the mirror line. 3
Rotation symmetry seems like the easiest of the four legal moves to describe, but there is one important factor never to forget. So rotation symmetry is another rigid motion on the plane that starts at a point and moves to another. Ok so it's not exactly that simple. A fact you must never forget: for something to rotate it must first have a fixed point which is called the rotocenter. 4 If we took a clock, for example, the rotocenter would be the fixed middle point, where the hour, minute and seconds hand are held together in the middle of the face with a screw. So everything rotates around that fixed point or else the clock's hands would fall. It works like an axle in the case of a 3-D shape.
Of course just like mirror reflection there are rules with rotation symmetry. You already know the first: that in order to have this type of symmetry there must be a fixed point or rotocenter. Secondly, the distance from the starting figure to the rotocenter is the same as the distance from the ending figure to the rotocenter. Most importantly, every point rotates through the same angle around the rotocenter. In math rotation angles are measured in a few different ways. One is as fractions of a full-turn and the other is by the degree of the angle of rotation. It is all dependent on what type of information you need to collect. Both are variations of the same thing. So if you want to describe it as fractions of a full turn then that is just basically measuring the angle. For example, ¼ of a full turn is 90 o, and 1/3 of a full turn is 120 o. But when considering the symmetry you measure it to find out how many turns it takes to get back to the identity transformation (starting point) or to the original starting point. This tells us how many repeats of the basic pattern one can expect to find.
The simplest of the rigid motions to visualize is translation symmetry. Basically in translation symmetry all shapes and figures are moved by the exact same distance as well as direction. Every line segment moves to a line segment of the same length, and parallel to the starting segment. Wallpaper designs are the best example of this type of rigid motion. Wallpaper is made by making a nice motif, then translating it over and over again, until it fills up the whole plane, or at least as much of it as you can see. It's not a bunch of different pictures and such randomly placed across the wall because that would be more like an art piece or a child with a crayon drawing on the wall. In most translation situations the pattern is easy to pick out, and it is easy to see how each shape moves throughout the design.
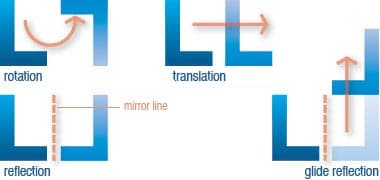
One of the goals of this unit is for my students to learn how shapes and figures move within a grid which includes moving things by those rigid rules, but also by combining those same movements. Translation followed by another translation always equals another translation. Also two mirror/reflection motions in parallel axes gives us a translation. A glide reflection is a mirror reflection followed by a translation parallel to the mirror. A pattern made by repeating a single glide translation looks exactly like foot prints in the sand.
So now we're down to the reason why this unit is being written: Wallpapers and the geometry within them. Wallpaper. I think about it and I must admit it has been a while since I've heard anyone tell me they're busy this weekend because they have wallpaper to put up. A favorite memory is of listening to people complain their walls weren't exactly even so the wallpaper wouldn't match up correctly, therefore, making the pattern off by a centimeter. Oh how I didn't know their pains until now while learning about all this stuff. We still have some up in my Dad's house from the 1980's that he just doesn't seem to want to take down. Maybe because it's a more formal room and wallpaper just adds to making it seem more formal? I really don't know, but I used to love lying on the rug and staring at the big flowers that repeated over and over again. I thought it was fun to look for the mistake in the pattern, but I never found it. Grouping things together with the tile on the bathroom floor and finding how many different ways to put it all together into a shape or formation was fun, and not once did I ever think of it as a geometry problem.
Wallpapers start not on an entire wall but with what are called strip patterns, or also Frieze Patterns. I would consider this the small strip of wallpaper my parents used at the top where the wall meets the ceiling. That strip that had one pattern that ran across it like a line. So it's the same thing over and over again. One cannot have a strip pattern of random images or else it would not be considered a "strip pattern". Shapes with translation symmetry run in one direction and one direction only – usually, horizontally. The top and bottom lines of every strip always stay the same distance apart and there is always an invisible center line called the median. Anything that preserves the strip preserves the median line; therefore, all the symmetries of the strip are the symmetries of the line. The median line can be a mirror of symmetry for the strip. Of course, the points on the line itself will not move, but the two halves of the strip will be switched. Every strip pattern must have translation symmetry, but this could also be combined with other options as well such as reflection (horizontal or vertical) or rotation (by half of a full turn, or 180 o, with rotocenter on the median line).
There are 7 symmetry types of Frieze Patterns that can exist on a strip 5
- "Hop": This looks like someone hopped on one foot along a straight line, and has only translational symmetries (see page titled "Frieze Patterns" example #1).
- "Jump": Act like a bunny rabbit and hop both feet together moving to the right. It includes translation symmetries and reflection in the median line (see page titled "Frieze Patterns" example #2)
- "Sidle": This includes translations and reflections in vertical lines (see page titled "Frieze Patterns" example #3).
- "Spinning hop": This requires making an 180 degree turn while jumping forward. It has translations and half turn rotations (see page titled "Frieze Patterns" example #4).
- "Spinning jump": This contains every possible symmetry: translation, horizontal and vertical reflection and rotation (see page titled "Frieze Patterns" example #5).
- "Step": This looks like foot prints in the sand, and includes both translational and glide symmetries (see page titled "Frieze Patterns" example #6).
- "Spinning sidle" has translation, glide and rotational (by half turn) symmetries (see page titled "Frieze Patterns" example #7). It has vertical reflections but not horizontal. The difference between this and #5 is in how the reflections are related to the rotations. In #5, the rotocenters are on the axes of vertical reflection. Here, the rotocenters are halfway between the vertical reflection axes.
The difference between wallpapers and strip patterns is simple to state: wallpaper covers the entire plane and a strip pattern is just an infinite strip. So wallpaper patterns have translation symmetry in two different directions. Those that have only translation symmetry are the most common and easy to pick out: the pattern such as the wallpaper at my Dad's house. Wallpaper patterns can also use all the various rigid moves as the strip pattern and, in fact, one can build a wallpaper pattern by stacking the same strip one on top of the other. This can be done in several different ways, which can have more or less symmetry. Wallpaper patterns can have rotational symmetry of order 1, 2, 3, 4 or 6, and only these. In addition, they may or may not have reflection or glide reflection symmetries. There are 17 types in all. You can always combine symmetries on wallpaper as long as the pattern remains unchanged and does not vary from the original pattern.
Teaching Strategies
As with any teacher those of us in special education have to be very sensitive as to how a lesson plan is constructed, so we must first look towards our audience. I have explained earlier that most students come into my room hating math and believe me I get why they feel this way. Frustration with not knowing all the proper steps or missing something small that causes the entire problem to be wrong. Yes, I understand because I remember not getting it. Having a classroom of students with learning disabilities is challenging and keeping them on task even more challenging at times. As I tell all teachers, being excited about the subject matter your teaching is just as important as your knowledge of it. Sure geometry wasn't my favorite subject, but I have grown to love and appreciate its challenges. For me it was working with the right program.
I believe in what is called the "direct instruction" approach to teaching math. According to the National Institute for Direct Instruction "Direct Instruction (DI) is a model for teaching that emphasizes well-developed and carefully planned lessons designed around small learning increments and clearly defined and prescribed teaching tasks. It is based on the theory that clear instruction that eliminates misinterpretations can greatly improve and accelerate learning." Sounds like a lot, but in reality it really isn't. Direct Instruction is structured so that you first start with the most simple of skills, master them and build upon what you have mastered to use for the next level. I think it's brilliant because it never leaves the students guessing and sitting frustrated at their desk. No student is asked to try something without first seeing the teacher do it. So the approach is something similar to "Teacher shows students, together they solve, student solves independently". The fact that it's consistent is important. The same vocabulary is used through out the lessons and no short cuts are taught until the students have mastered doing something the long way. I strongly feel that students should not be asked to figure out how to work problems without first having several examples worked out for them by the teacher. That's where most of the frustration comes in. According to the Institute for Direct Instruction most students' biggest problem is that they are given a math equation and they have no clue where to start. Once that happens they just kind of give up. What's the first step to solving this problem? With the Direct Instruction approach they are only asked to work the first step. They master "getting the first step" and then move on. One step at a time. Plus since my program is scripted (which I do like) it becomes a more interactive way to teach. We have a call and respond method which I find keeps the students from getting bored and I can quickly tell if they are getting it or not because it's instant feedback. So my lesson plans will be structured based on the Direct Instruction model of learning with a few personal twists because I also think math should be fun.
I believe the best way to introduce a new subject is to relate it back to things that are familiar to students. For example every year in English class I pick one book that takes place in the San Francisco Bay Area because the setting will be familiar to the students and, therefore, the story becomes higher interest. When introducing symmetry to the students I will use examples from various famous and familiar sites from the area such as the Golden Gate Bridge, Coit Tower, AT&T Park and the Terra Nova High School building, to name a few. Since both my students and I are visual learners I will have pictures taken of the various sites and ask the students to explore the pictures and try to find patterns within the structures and outline them with a marker. Afterwards I want to have the students talk about their findings to the rest of the class. I never remember talking about math when I was a student, and I have come to strongly believe, especially since working with Professor Howe, that math is a very verbal subject matter. It is one thing to be able to solve the problem, but something entirely different to put it into words. To be able to use one's vocabulary to teach another person how to do something is very powerful and the true test of understanding. Most adults can tell you 2 + 2 = 4, but what is 4 exactly? 4 is only a character to represent something else and it is important to be able to identify what that other thing is using one's vocabulary. These lesson plans will not only have the students talking about symmetry, but also give them visuals they can refer to support different learning styles. Again as a visual learner I find having both the verbal and visual support only enhances one's learning.
Students often ask me, how all this relates to their lives? I understand why they ask because like so many people I feel as if I have a limited amount of space in my memory bank for information. What I want is to have the ability to filter the important information with things that are nice to know, but not very useful in my life. This is why with most new concepts I present to the students I also make sure they understand how this is important in their everyday or future lives. Why bother with trivial stuff when there are other things that do make a difference? Students need to understand that geometry is what keeps a building from crumbling to the ground, or keeps the roof over our heads through a method of calculated angles and support beams which are measured and determined through basic geometry and symmetry. That can easily be demonstrated by building a simple house made of cards, which stands up solely because the angles and cards are placed in perfect geometric order. One mistake and the entire thing falls. The same with the game Jenga where players have to pull out wooden blocks without knocking down the entire tower. The house of cards could also be built on grid paper so the students can figure out the optimal distance between the cards, so as to again show symmetry within the structure they are creating.
Also, the Tetris computer game uses geometry. Then I remind them if it wasn't for geometry they would be taking math class outside instead of in the classroom because it's the angles that hold the building up. A football is also a good example of geometry. The shape of the ball and the angle at which you throw it will result in either a perfect spiral or something no one can catch. Where ever there is an angle geometry is present. I asked the same question when I was in school yet no one could explain it to me. So having a practical reason to learn geometry is a great way for them to buy into the importance of getting to know the basic subject. While there is very much a strong science to geometry that is not something I plan on covering in my unit, but I could very well see working with the science teachers to plan on presenting my lesson plans at the same time they are covering it in class. This I plan on exploring once school starts so that the students can see the same thing taught across different subjects, as well as two different teachers. Introducing the practical side of geometry should be done in a fun manner. Since special education consists mainly of boys and a few girls it would be fun and create a lot of interests to make it into a game. Since football is the biggest sport at Terra Nova and I always have a few players in my classes we could start here. Games are a great and fun way to introduce any new subject especially if you don't really tell the students why they're playing the game at first. So my plan is to put the students into groups (size depends on the number of students in class as well as those with experience throwing around a football) each group would have a team leader who would write down all the important things they would tell someone if they had to teach them to throw the football. Each student leader would then present it to the class while a recorder posted each point on the white board. Then I would take it outside and make a game of it by having each student leader show the others how exactly to throw the ball while explaining the importance of using angles while throwing. Making it all into a contest is always fun and increases the student's interests.
I believe strongly that education can and should be fun and challenging all at the same time. There has to be a practical side to everything and it all has to balance out. While I do like to play games lecture time is essential. As I put together the unit it is good to incorporate media as well. So I do use either an overhead projector or power point to present certain information to my students. I always remembered being bored in math class. Yes, that was partly because I didn't get it all the time, but it was also because the teachers presented it with no passion or love of the subject matter. By combining physical games, video games and board games, my lessons connects to all types of students and pique their interests, but just like as with symmetry there has to be a balance. Students will be asked to work problems in their notebooks as presented to the class by the teacher. They will later be tested as to knowledge of the material once each step has been mastered in order to keep track of the benchmarked goals (or the mini goals of each lesson plan) of the unit so if something needs to be reviewed it can quickly be done before the end of the unit.
My final project will be an art piece that each student creates themselves. It wasn't easy to come up with something that both tested their knowledge yet incorporated some type of creativity on their behalf. One of the many reasons why I have enjoyed learning about symmetry is the fact that there is so much art surrounding it. Not just that, but I've been living with it my whole life and never had an understanding or respect as to how it worked.
Students will be asked to visually identify all the rigid movements on paper through looking at examples. I do believe it is important for them to not only be able to see and identify, but create it themselves. So while they will have a test the art project will be the tell tale sign they understand the unit.
As a final project each student will be asked to create wallpaper for 3 of the 7 Frieze Patterns. They will be allowed to use the computer or draw it on paper, whichever they prefer. Then they will be asked to list all the symmetries used in the wallpaper and explain how it was used. I will be expecting each student to make it colorful and stay true to the pattern they design. It can be kept simple or complex depending on their inspiration.

Comments: