Content Objectives

Introduction

For years, I had noticed the same misconception among my third grade students. The first few years it took me by surprise. After that, I knew to expect it, but simply didn’t know what to do to help them. Finally, last year, I couldn’t take it: I had to learn a better way to teach.

What was this mysterious concept my students struggled to understand? Finding the difference when comparing two quantities. Within the first week of my curriculum’s scope and sequence, there it was, the question lying in wait, ready to trick thirty unsuspecting children, silently mocking me: “John has 5 toys. Maria has 9 toys. How many more toys does Maria have than John?” Of the puzzled set, some students found the sum of 5 and 9. Others, more confident in their reasoning, simply believed the answer to be 9. Others correctly found the answer (“Four more toys!”) but only by counting up from 5 on their fingers.

According to the Common Core State Standards, students should be able to master a question such as this one by the end of first grade.¹ An analysis of the previous year’s assessment data revealed that my students were, on average, entering my classroom above grade level in math. In many ways, they were quite proficient. Yet my lessons rarely stuck; at one point, I found myself simply saying the question slower and louder (“How… many… MORE… years…?”), hoping my accentuation of a key word would be enough to do the trick. It wasn’t. I knew something had to change.

This unit is the result of an extensive period of research and planning to get at the heart of my students’ struggle. I wanted to find out what a deep understanding of addition and subtraction would look like in the early elementary grades, so that a third grade student could successfully apply these operations in a wide variety of contexts and problem types. Further, I sought strategies that would help students model the relationships between the quantities within these problems, in order to make sense of and ultimately solve them.

My unit has three overarching goals. First, I want students to be able to reason conceptually about when and how to use addition and subtraction in a wide variety of word problems. Among these problem types, I will place the greatest emphasis on the problem type I’ve described above: comparing two quantities. My second goal is for students to successfully use pictorial models to help them in their reasoning about quantities and their relationships within these word problems. Finally, I want students to be able to use what they have learned about modeling with diagrams to solve two-step addition and subtraction word problems.

School Setting and Background

I teach in a large, urban, neighborhood elementary school. My students are predominantly Mexican-American, while all qualify for free/reduced price lunch. Approximately half of my students are English Language Learners. Our school uses a transitional bilingual program. Students in pre-kindergarten and kindergarten receive instruction predominantly in Spanish, transitioning to English gradually over the primary years. In my third grade classroom, I conduct whole-class lessons mostly in English, while using Spanish to clarify and reiterate key concepts and vocabulary. I also use Spanish in small groups and one-on-one for targeted support of particular students. Since this curriculum unit focuses on research on math content and teaching methods, I do not go into detail about bilingual teaching strategies, but instead focus on the mathematics involved in the unit.

A Taxonomy for Addition and Subtraction Problem Types

The Common Core State Standards provide a useful taxonomy for understanding the main kinds of contexts in which we can use addition and subtraction.² These contexts fall into three categories: change, comparison, and part-part-whole. In change problems, some quantity is either added to or taken away from another quantity over time. In comparison problems, there is a numerical difference between two fixed quantities. In part-part-whole problems, there are two or more component quantities that, when taken together, make up a total quantity.

Within the family of change problems, there are two subcategories: change-increase, in which a quantity is added to an initial amount, and change-decrease, in which a quantity is taken from the initial amount. Further, for each of these two subcategories, there might be one of three possible unknowns. For example, take a change-increase scenario: 3 turtles sat on a log. 4 more turtles joined them. Now there are 7 turtles on the log. Depending on which number is left out of this problem, one could find an unknown initial amount (? + 4 = 7), an unknown amount of change (3 + ? = 7), or an unknown final amount (3 + 4 = ?). Similarly, a change-decrease problem might also have one of three possible unknowns. For example: 10 cows graze in a pasture. 2 cows leave. Now there are 8 cows in the pasture. Again, depending on what is unknown, we might solve for the initial amount (? – 2 = 8), the amount of change (10 - ? = 8), or the final amount (10 – 2 = ?).

  Comparison problems can also be categorized into two subgroups: comparison-more, in which two quantities are compared using “more/greater than” language, and comparison-less, in which two quantities are compared using “less/fewer than” language. Once again, within these two subgroups, there can be three possible unknowns. Let’s consider the comparison-more scenario that I showed my students: John is 5 years old. Maria is 9 years old. Maria is 4 years older than John. Depending on which number is withheld in the problem, one might need to find an unknown lesser amount (? + 4 = 9), an unknown greater amount (5 + ? = 9), or, as was the case in the story about my students, an unknown difference (9 – 5 = ?). The same situation can be expressed as a comparison-less problem, provided that we rearrange the two amounts so that we use “less than” instead of “more than” terminology: John is 5 years old. Maria is 9 years old. John is 4 years younger than Maria. Again, there are the same three possible unknowns.

Part-part-whole problems feature a set of two or more different quantities that, together, compose a whole quantity. This problem type differs from the change problem type because both quantities are static, whereas in a change problem, there is an initial quantity and a change in that quantity over time. A part-part-whole problem can have one of two possible unknowns: either one of the parts is unknown or the whole is unknown. There is no specified ordering of the parts. For example, consider: There are 4 yellow fish and 2 red fish. There are 6 fish altogether. Either one of the parts may be unknown (? + 2 = 6 or 4 + ? = 6) or the whole may be unknown (4 + 2 = ?).

Using the Taxonomy to Investigate Misconceptions of Addition and Subtraction Problems

In all, the taxonomy distinguishes 14 problem types in which addition and subtraction might be used. No wonder my students were confused. In the course of my research, I found out that they were not alone. John Van de Walle, in Elementary and Middle School Mathematics: Teaching Developmentally, explains that it is very common for students in the primary grades to develop an incomplete understanding of addition and subtraction.³ Through exposure to various problem types, students should understand what Randall I. Charles calls one of “big ideas” of elementary mathematics: addition and subtraction can be used to solve problems of the three types categorized in the taxonomy.⁴ Yet it is all too common for students to develop an understanding of these operations that is limited to change and part-part-whole problem types. In other words, students believe addition only means two amounts are put together, and subtraction means an amount is taken away.

Why is this the case? It turns out that comparison problems are more difficult than the other types. One reason is because comparison problems feature a quantity that does not exist concretely. If Ashley has 11 cards and Brenda has 7 cards, then how many more cards does Ashley have than Brenda? Some students have trouble actually seeing that there is an “extra” derived from these quantities. The “4 more cards” does not represent 4 specific cards, but rather the range between the quantities of cards that each girl has.

Further, unlike the other problem types, comparison problems are static. Nothing is coming together or being taken apart. As a result, there are often no clues in the wording of a comparison problem that uniformly suggest a particular operation to use. This is why some researchers suggest that using “equalizing” language might lower the difficulty level of a comparison problem. In this case, we might ask: “How many new cards does Brenda need to get so she will have the same number of cards as Ashley?” This wording suggests an action to take to find the solution. Using this type of equalizing language is a useful strategy to help students understand the meaning of comparison phrases such as “How many more?”

Another example of a challenge posed by comparison problems is how the words “more” or “less” interact with whether the unknown in the problem is the smaller or larger quantity. Consider these two examples, both using the word “more”:

• Alexis has 6 toy cars. Katrina has 3 more toy cars than Alexis. How many toy cars does Katrina have?

• Jennifer reads 12 pages in a book. Jennifer reads 4 more pages than Bryan. How many pages does Bryan read?

Problem (a) has a “consistent” format: the language of the problem (“more”) is consistent with the operation (addition) that we can use to find our solution (e.g., 6 + 3 = ?). This is because the larger number (Katrina’s toy cars) is what is unknown in the problem. Adding the difference to the smaller number will yield the larger quantity. In contrast, problem (b) is “inconsistent” because the word “more” is opposite to the operation that might be used to solve the problem (e.g., 12 – 4 = ?). When a child sees “more,” he is likely to think “addition.” But since the smaller number (Bryan’s pages) is unknown, we must subtract the difference from the larger number in order to find it. Research shows that students are often misled by inconsistently worded comparison problems, revealing a lack of understanding of the relationships within the problem. Indeed, using the opposite operation tends to be the most common type of error for second grade students. Meanwhile, research shows that first graders who make errors in comparison problems are more likely to choose a number from the problem and not perform any operation at all.⁵ So it’s no surprise that these two types of errors I continually saw among many of my third grade students!

Modeling with Mathematics

So those are some of the problems. But what’s the solution? How can we help students successfully reason about quantities and their relationships within a wide variety of word problems? What tools and strategies can we use to help students make reasonable choices about how to use addition and subtraction to find their solution? I researched a variety of pictorial diagrams that can be used to help students reason with quantities and their relationships. I chose the model method, famously used in Singapore Math, as the main tool I would teach my students to use to make sense of word problems.⁶

But first, some background on modeling in mathematics. Pictorial models are simply another way of representing the information given in a word problem. They are helpful for children to use because, as I have described above, the information given in a word problem is often not clear enough to students that they can readily find a solution. As teachers, we can try rewording the problem, emphasizing certain words, even just reading it all again slower and louder. The results will be limited at best. Instead, what students really need is a “re-presentation”—literally, another way of giving the information. Visual diagrams help make clear to students the information that remained hidden before. With this new knowledge, students often have enough insight to make a reasonable choice about which operations to use, and with which quantities.⁷

According to the Singapore model method, students use bars of varying lengths to show the quantities given in a problem, as well as the relationship between those quantities. Within the three families of one-step addition and subtraction problems, there are two types of bar models that are typically used: a one-bar model for change and part-part-whole scenarios, and a two-bar model for comparison. (It is worth noting that two-bar models can also be used for change and part-part-whole; it might be useful to use a two-bar model to emphasize the relationship between these scenarios and comparison scenarios.) Here are two examples of how these types might be depicted.

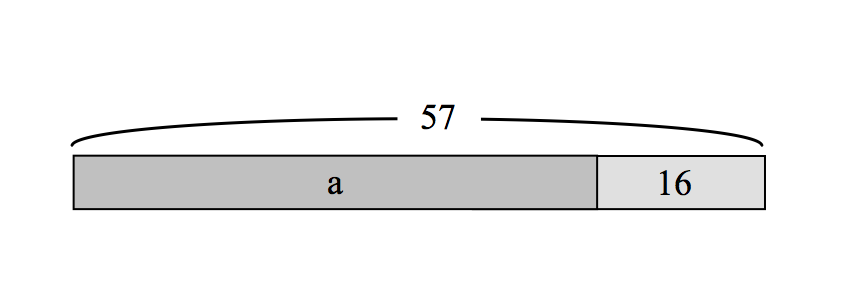
Part-part-whole (part unknown): There were 57 second and third grade students in the art show. 16 of the students were in second grade. How many were in third grade?

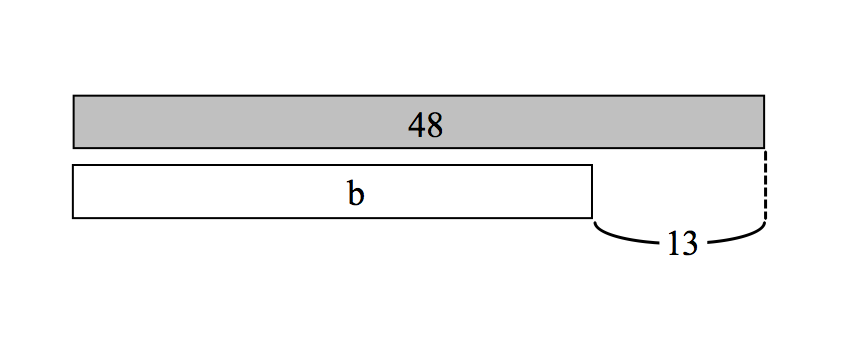
Compare-more (lesser amount unknown): Jose has 48 crayons. Jose has 13 more crayons than Samantha. How many crayons does Samantha have?

When students take information from a word problem and represent the given and unknown quantities as bars of different lengths, they can then make reasonable choices about how to use an operation to find what is unknown. The bar lengths are a visible way of keeping track of the quantities within the problem, so students can return to them naturally to check the reasonableness of their solution. And using this modeling method has proven effective. Lisa England studied the performance of students on a test of one- and two-step addition and subtraction problems. She found that, on average, the students who were taught to use bar models over only four weeks of instruction outperformed their peers on nineteen of the twenty test questions. These students also improved at a greater rate from pre-test to posttest than their peers in a gifted class that did not use the model method as part of instruction.⁸

It is important for teachers to introduce this type of modeling in a gradual, developmentally appropriate way, in order to transition students from concrete to semi-concrete thinking. For example, students first tend to line up counters to show the two quantities in a word problem. I would model for students how to draw small circles within a line of boxes on grid paper. This transition introduces the possibility that these discrete circles, when lined up, can be the basis for a rectangle of a certain length. As bigger numbers appear later in the curriculum, I help students complete the transition to the bar model. A helpful example of this transition appears in the Japanese curriculum Mathematics International. In a word problem about oranges, an image shows circles lined up within rectangles, and then an image of the rectangles without their circles. A helpful caption reads: “Although oranges are countable objects, we expressed the quantity using length in the diagram.” Using this progression, I help students move from using counters, to drawing representations of counters, to simply drawing lengths to represent quantities.⁹

Two-Step Addition and Subtraction Problems

Once students understand the model method, they can use bar models to reason through increasingly complex word problems, such as two-step addition and subtraction problems. We can create a wide variety of these two-step problems by choosing any two one-step problems from the taxonomy described above and incorporating them into a scenario with some known and unknown quantities. Two-step problems are more complex because they require students to keep track of multiple relationships between quantities. Often, one unknown must be found first so that this value can be used in the problem’s second step. Further, there are multiple aspects to a two-step word problem that might affect its difficulty level, such as: the level of difficulty of the component one-step problems; which unknown needs to be found first in order to perform the second operation; and the order that the known and unknown values are presented in the wording of the problem.

Let’s consider an example in which we join the types: change-increase (unknown final) and compare-more (unknown lesser amount):

At the end of the first half of the basketball game, the red team had 36 points. In the second half, the red team scored 29 more points. At the end of the game, the red team had 17 more points than the blue team. How many points did the blue team score?

Now let’s examine how we might represent these quantities using a bar model:

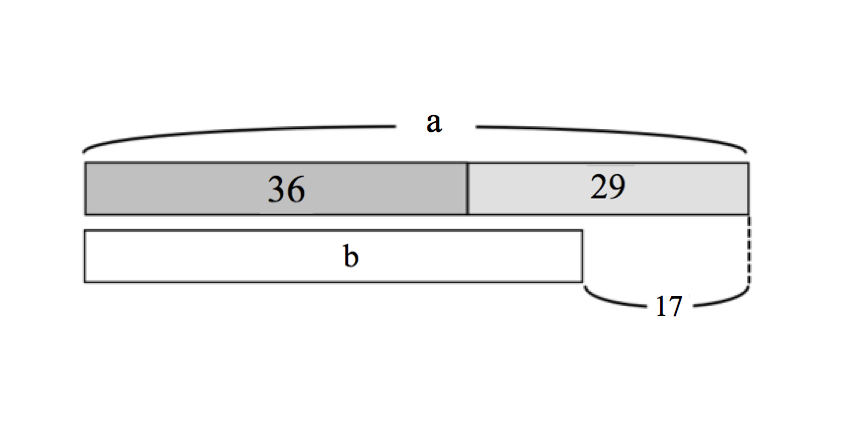
Examining this model, a student may decide to first solve to find the total number of points scored by the red team (36 + 29 = 65). Although the problem does not pose this question directly, the model makes visible the idea that finding this sum may be a helpful first-step in solving the problem in its entirety. Once a student finds the red team’s total, or the length of the top bar, she can subtract the difference (65 – 17 = 48) to find the blue team’s total points, or the length of the bottom bar.

An additional benefit of using the bar model is that students may see alternate solution paths that they would not have considered from solely reading the word problem. For example, when comparing the two bar lengths, a student might notice that finding the length of the top bar is unnecessary. Instead, she might temporarily assume that both teams scored the same number of points in the first half, and simply subtract the difference in total points from the red team’s second half points (29 – 17 = 12). The result would be one of many possible combinations of first half points (36) and second half points (12) for the blue team. Their sum would provide the blue team’s total points (36 + 12 = 48).

Finally, given the difficulty of two-step problems, Van de Walle recommends that teachers help their students focus on finding the “hidden question” within each problem’s context.¹⁰ One way to do this is by first breaking up a two-step problem into its two one-step parts and composing a question for each part. In the example above, we might stop after the first sentence to ask, “How many points did the red team score in all?” By focusing discussion around this question and by drawing attention to its “hidden” nature, we can help students understand the fundamental structure of two-step problems. With practice, students will use this understanding to systematically approach these problems on their own.

Teaching Strategies

Thinking Thematically: Everyday Classroom Scenarios

Throughout this period of research and planning, I considered not only the content to be taught but also the structure of the unit itself. My first decision was to organize my unit around a topic that my students would be both familiar with and excited by. My initial reasoning had to do with knowledge of my student population. 22 of my incoming 27 students are English Language Learners. Research supports the idea that these students learn better when they are able to make connections from day to day within a unit. As lessons proceed, students can draw upon what they learned earlier to steadily build their schema around a topic. With this in mind, I chose the theme of using addition and subtraction to address everyday classroom and school-based scenarios.

Why this theme? For one, I will be teaching this unit at the start of the school year, an exciting time for third grade students. Each day they reacquaint themselves with the structures and systems of the school and their classroom. At my school, early September finds students renewing their excitement over rituals such as tracking their classroom’s days of perfect attendance or counting their number of personal “Caught Being Good” tickets to earn a small prize. Meanwhile, students receive new classroom jobs such as distributing laptops from the computer cart to their classmates or filling out the daily lunch count.

In all of these scenarios (and many more), students can develop and put to use their understanding of the relationship between addition and subtraction. As such, my choice to build a unit around these everyday classroom scenarios takes advantage of my students’ natural excitement for the topic. My choice to make use of these scenarios also makes sense from a mathematical perspective. These activities make up the daily experience of my students at school, and, as a result, my students already have their own strategies and ideas around how to count or track the quantities involved in these scenarios. These personal strategies will be great starting points for building deeper understanding and will provide great fodder for student discussion. Finally, these problem scenarios will be useful because they are relevant throughout the entire school year and so can afford my students many opportunities for revisiting and practicing the mathematical concepts addressed in the unit.

Thinking Structurally: A Progression of Learning

Having a theme is not enough, of course. Throughout my planning, I also considered a number of possible progressions for how I would introduce and develop both the theme and the content. Given past experience, I was pretty sure I would enter my classroom and encounter a number of students who struggled to solve first-grade level comparison problems. I wanted to structure my unit to ensure that, after a few weeks of learning, these same students would be quite adept at solving two-step problems of various types and combinations.

My unit will begin with an introduction to the theme. I will present my students with vignettes of a few classroom scenarios and ask for ideas about what the student in the story should do. An example might be: “Michael is taking the lunch count and needs to know how many students are in class. He looks around the room and sees three empty desks.” This simple, broad description of a scenario can be the basis for an interesting discussion about quick and effective approaches. Michael can count the students he sees one by one. He can count the boys and girls separately and find their sum. Or, more efficiently, he can take the total number of desks (given there is one for each student) and subtract the number of empty desks. Together the students will brainstorm a list of scenarios in which they can use addition and subtraction and at school. This ongoing list will become an anchor in my classroom, a tool to continually reinforce the real-world context of the unit’s content.

After this introduction, the unit will progress according to two main phases, each with its own type of assessment (Figure 1). In the first phase, I will deliver a series of lessons on one-step problems, with more time and attention paid to comparison problems. When teaching these problems, I will scaffold rigor by first beginning with “equalizing” language and moving on to static wording, as described above. It will be during these lessons that I introduce the bar model and help my students use it to reason through quantities and their relationships. Modeling will be especially helpful for students to reason through the more challenging “inconsistent” problems. Knowing that my students will benefit from continued exposure to a wide variety of these one-step problems, I will formally assess them at this point in the unit by asking them to create a “workbook”; each student will develop a problem about a school scenario as well as create an answer key that shows a clear method for solving. I will compile these examples so that students can get further practice by solving the problems of their peers.

In the second phase, students will learn to solve two-step problems, which I will scaffold according to difficulty. This means I will begin with easier one-step component problems, such as change and part-part-whole types, and later combine the more complex “inconsistent” comparison types. As they continue to develop what they have learned about bar models, my students will be able to visualize the multiple quantities and relationships within these increasingly complex scenarios. In this phase, I expect students to discuss multiple solution methods and justify their strategies by referring to their models. It is my goal for students to be able to decompose these two-step problems as a chain of two simpler problems linked by an unknown. Only after they solve for this first unknown will they have enough information to solve the problem in its entirety.

The unit will culminate with a summative assessment of questions for both one- and two-step problems. I will conduct an item analysis to determine which problem types, or combinations of problem types, were easiest for my students and which were most difficult. This information will help me decide which problems my students still need to practice, as well as determine which students are in need of continued support. Later in the year, I will teach a similar unit in which I help students use modeling to reason through various one- and two-step multiplication and division problems. The results of this assessment will help me make decisions about how I might bridge my students’ understanding of addition and subtraction toward a full understanding of multiplication and division.

Structured Problem Solving

So far I have described the theme of the unit and the progression of its lessons. Yet there are more variations in types of problems than I could possibly show my students during this time. How, then, would it be possible to achieve the goal for students to be able to solve any individual addition and subtraction problem they come across? The purpose, ultimately, is for students to develop the habits of mind of analyzing and reasoning through all the types of problems so they can approach any addition or subtraction problem successfully. To develop and transfer this level of higher-order thinking, students must experience regular problem-solving-based lessons and routinely compare and discuss the reasoning behind various approaches to problems. To achieve this end, I use a routine called “structured problem solving” as the daily approach to mathematics instruction in my classroom.

Common in Japan, the purpose of structured problem solving is to both generate interest and excitement in math and to help students develop and discuss ideas that yield robust understanding of math content. Lessons begin with the introduction of a carefully worded problem. Students work alone, or sometimes collaboratively, to solve the problem using what they already know. Next, the teacher selects certain students to present their solution methods to the class. These methods provide the basis for a whole-class discussion in which students compare their mathematical ideas. The teacher facilitates this conversation to help students pull their ideas together and arrive at some new learning. Near the end of the lesson, the teacher helps the students summarize their learning. Finally, students often reflect on what they have learned in a math journal.¹¹

There are three important features of a typical structured problem solving lesson: careful creation and delivery of a problem, facilitation of classroom discussion, and strategic display of student ideas. Below I will describe each of these features and how I use them in my classroom.

To create a good problem, a teacher should think about what would motivate the students to want to solve it. It is not enough for students to want to find a solution only because their teacher expects them to. A good problem should also present some exciting tension that the students are eager to approach and ultimately resolve. This tension should arise from the context of the problem itself and from how the teacher chooses to present the problem. For example, my class gets an extra recess block as a reward after they accumulate 25 days of perfect attendance. Before presenting my students with a problem about how many days remain before they will get their incentive, I might first ask them what games they would play during an extra recess period or to estimate how soon they think they can accumulate their 25 days. I have found that the excitement the teacher builds when leading up to the question in this way can often propel students into an eager mathematical investigation of the problem itself.

In Japan, the facilitation of classroom discussion is referred to as neriage, literally “kneading” or “polishing.” In other words, the artful teacher uses discussion as a way of “polishing” student ideas so that what is produced is a refined understanding of the concept at hand. In my opinion, quality neriage is one of the hardest things I do as a teacher. It begins before the lesson, when I decide what exactly I want my students to learn and then think about all the ways they might try to solve the problem. While students solve, I observe the students’ solution methods and choose a handful of different ideas that I think will help move us toward the new learning I have planned. I then select certain students to present these ideas to the class, using a sequence that I think will help students move from a simple to a more sophisticated understanding of the concept. Then the real work begins. I ask questions that get students to compare the mathematics within each of the solution methods, so that the class arrives not only at a correct solution, but a robust understanding of the mathematics that got them there. Of course, given the complex and at times unpredictable nature of student thinking, this process is a mixture of planning and improvisation, anticipation and reaction. This is what makes neriage so challenging, but also so thrilling.

The third feature of structured problem solving involves how the teacher displays student ideas on the board. Ideally, the board work should develop strategically to “tell the story” of how the mathematical understanding developed throughout the lesson. Ideally, everything written and posted on the board stays there. Nothing is erased. Typically, I begin with a captivating image that has to do with the context at hand, in this case a classroom scenario. Once I build excitement about this topic, I introduce the problem and write it alongside the image. Before releasing the students to solve, I might survey the room for some initial solution ideas and make a list of these possible methods under the problem. Later, as students present their ideas, I carefully represent each student’s method on the board in a way that makes their thinking visible. Once all strategies are up, these became the central reference points for class discussion. I continue to add important student ideas and key points as they arise during discussion. At the lesson’s end, I synthesize the new learning in the form of a summary on the right side of the board, often posing a reflection question alongside the summary (see Figure 2).

Figure 2: Board display for a lesson on finding the area of L-shaped figures.

Classroom Activities

In this section, I will “zoom in” on my plan for two lessons from the unit. The first, Lesson A, is a lesson on reasoning through comparison problems. This lesson will probably take place at the end of the first week of instruction. Later, in Lesson B, I will describe my plan for an introductory lesson on solving two-step problems.

Lesson A

In Lesson A, my objective is for students to see the difference between two comparison-more problems, one with the larger value that is unknown and one with an unknown lesser value. Through comparison of their strategies and discussion, I want students to see that surface-level “tricks”—such as adding the two known values because they see the word “more”—do not always work. In the end, I will sum up our discussion by reiterating that it is necessary to first understand the problem, that is, to make sense of the relationships between the quantities in a problem, before choosing an operation to solve.

To produce a discussion that would lead to this new learning, I will present two similar problems at the start of the lesson. As you will see, the problems below are nearly identical in scenario, wording, and number:

• Comparison-more (larger amount unknown): At the Chavez Carnival, some third-grade students are playing soccer. There is a red team and a blue team. 9 kids are on the red team. Some new kids ask if they can join the game. If 3 kids join the red team, they will have as many kids as the blue team. How many kids are on the blue team?

• Comparison-more (lesser amount unknown): Later at the carnival, some second-grade students are playing soccer. There is a red team and a blue team. 9 kids are on the red team. Some new kids ask if they can join the game. If 3 kids join the blue team, they will have as many kids as the red team. How many kids are on the blue team?

First I will build up background knowledge about our school carnival—one of the most memorable events of each school year—and then present the two problems. I will build tension and humor in the classroom by feigning ignorance: “I see the same numbers, the same words… These problems are the same, right? Do we need to solve both? Maybe we can save time by just answering one?” Inevitably, there will be some students who have caught on that there is a key difference between the two. Otherwise, why would their teacher present them with two problems that seem identical?

After asking for a few initial ideas to get us started, I will have students organize their notebook pages by drawing a line down the center, reserving a separate space on each side for their diagrams and number sentences. Then I will give 5 to 10 minutes for independent problem solving. Afterward, knowing that most students will solve problem (a) correctly, I will call one student to present a bar diagram and correct solution for this problem first. After confirming that the diagram and solution are reasonable, we will move on to problem (b). But first, here is where more drama can help whip up enthusiasm: “Maybe we should stop here? Was I right? Both are the same?” The class will surely be divided on whether the results were the same to both problems. I have found this type of tension is a great way to generate investment in the lesson.

For problem (b), I will call two students to present their diagrams and solutions. One will be a correct representation and solution, while the other will show the common error of choosing the wrong operation. After both solution methods are presented, I will ask questions that encourage students to make sense of the quantities and relationships within the problem. This might be one path of questioning within this section:

• I see two different solutions. Could both be correct? No? Why not?
• Let’s make sure we understand the methods. Can someone use the bar models to explain ______’s method? How about _____’s method?
• Let’s look more closely at the bar model. What does the length of each bar tell us about the two teams? Can you show us what each number in this model represents in the problem?
• How are the two approaches similar? How are they different?
• What do you see that makes sense to you based on your understanding of the problem?
• (Again, feigning ignorance…) I still don’t understand. Why did _______ subtract? The problem says “more.” Wouldn’t it be better to add?
• Which of these problems was easier? Harder? Why?

At the end of our discussion, I will sum up our learning and write a summary statement such as this on the board: When we read word problems, it is important to carefully study the relationship between the numbers before we start adding or subtracting. A bar model helps us to be sure. Students will write down this statement. I will accommodate for students who write slowly or have difficulty copying from the board, by giving out the summary on a paper strip that can be easily glued into their notebooks. Then I will ask students to reflect on what they learned in the lesson. Early in the year, I use sentence starters for the reflection, such as: “Today I learned…” Figure 3 shows a plan for the layout of the board.

Figure 3: A possible board plan for Lesson A.

Lesson B

Lesson B is the first lesson in which I formally expose my students to two-step problems. My objective is for students to begin to see the structure of this type of problem and to understand that it is sometimes necessary to perform a calculation more than once. I created a relatively easy problem by joining a change-increase with a change-decrease problem:

Change-increase (final unknown), change-decrease (final unknown): At the start of the school year, there were 27 students in a class. In the fall, 5 new students joined the class. In the spring, 3 students left the class to go to another school. How many students were in the class at the end of the year?

In this lesson, the format will be the same as in Lesson A: intro to the problem, problem solving, presentation of strategies, comparing and discussing, summarizing and reflecting. Here is the bar diagram and strategy I plan to discuss with students:

A correct solution method would be to first perform 27 + 5 = 32 and then 32 – 3 = 29. I will also choose students to present incorrect solution methods, such as 27 + 5 + 3 = 35. When comparing the methods, I want to keep students focused on what each bar and each number sentence represent from the problem. As discussed above, I also want to draw students’ attention to the “hidden question” within this problem’s context. A path of questioning might be:

• Let’s make sure we understand the methods. Can someone use the bar models to explain ______’s method? How about _____’s method?
• What do you see here that makes sense to you? Can you explain why it makes sense?
• Is it okay to add up these three numbers? What would that mean is happening in the problem? Does that make sense with today’s problem?
• Is there a question that is “hiding” in this problem? Who can explain it?
• How is this problem different than last week’s problems?
• Can you think of another way to solve this problem?

I will help students sum up their learning with a statement such as: We can think of some problems as two one-step problems put together. We may need to add or subtract more than once! As always, I will ask students to reflect on their learning and then ask a few students to share their ideas with the class. Figure 4 shows a possible board plan for this lesson.

Figure 4: A possible board plan for Lesson B

It is important to note that this is a very gradual introduction to two-step problems. One reason this problem is relatively easy is because finding the “hidden question” is not a crucial step in solving the problem. Some students may think of the problem as 27 + 5 – 3 = 29, and may not need a bar diagram to make sense of these operations. The simple nature of this problem allows me an opportunity to gradually introduce the idea of the “hidden question.” For example, I might ask the students if they can find the number of students in the class after the fall. Students should be able to explain that they can use this new quantity (32 students) to help them find the number of students at the end of the year. By using this lesson to turn students’ attention toward this hidden quantity, I can help ease their transition toward more complex problems in which finding the “hidden question” is a necessary step toward finding the solution. Throughout the unit, I will continue to expose my students to progressively more complex problems, until I feel they have become sufficiently proficient in analyzing problems that they will be able to successfully approach most any two-step problem they come across.