Lesson Plan 2
Standard
The student understands the structure of standard measurement systems, both SI and customary, including unit conversions and dimensional analysis
The student evaluates and analyzes formulas and functions of many kinds, using pencil and paper and more advanced technology.
The student rounds numbers used in applications to an appropriate degree of accuracy.
Rationale
Students need to understand that Astronomy is not a great mystery. Using simple Mathematical formulas, we can use data to calculate distances to stars.
Launch
Questions regarding the previous lesson and homework will be discussed.
What is the longest trip that you have ever been on? How long did it take you? When you look into the sky, how far
away do the stars seem? Do you think you could travel to a star? Discuss briefly some history of attempts to
calculate distance to stars. Explain stellar parallax. Do the hand activity to illustrate parallax. (See Overview)
Using Illustration 1, derive the formula 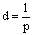 . Explain
the units of measurement. Discuss proper motion using Illustration 2.
. Explain
the units of measurement. Discuss proper motion using Illustration 2.
Explore
Provide each group with a star and the measure of the parallax angle. Have them calculate the distance to their star. When each group is finished, ask them to convert their answer from parsecs to light years. Then have them convert their answer to kilometers and then to meters. Then have them convert from parsecs to miles. Work should be shown for the conversions as taught in Lesson 1.
Each group presents their work to the class. The data is collected into a chart on the white board or a transparency or a giant writing pad. This needs to be kept where it can be used for Lesson 3.
Summarize
How far was the closest star? How does that relate to the longest trip that you have ever taken? How long do you think it would take to reach the closest star? Do you think that could be done in your lifetime? Why or Why not?
Homework
Students will be given 5 stars and their parallax angle measurements. They will do the same work that they did in class including the unit conversions.
Lesson Plan 3
Standard
The student understands the structure of standard measurement systems, both SI and customary, including unit conversions and dimensional analysis
The student evaluates and analyzes formulas and functions of many kinds, using pencil and paper and more advanced technology.
The student rounds numbers used in applications to an appropriate degree of accuracy
Rationale
Students need to understand that Astronomy is not a great mystery. Using simple Mathematical formulas, we can use data to calculate the luminosity of one star in relation to another star whose brightness is known.
Launch
Students are given the formulas for the area of a rectangle and the area of a trapezoid. The first formula is to be solved for h. The second is to be solved for b 2. The results are presented by different students. Discuss the importance of using good Algebra skills to complete this task.
Using the example of area of a circle from the Overview, illustrate how taking two equations and creating a ratio can result in a simpler equation.
Refer students to the chart created in class yesterday. Which of those stars do you think would be the brightest? Why do you think that? Groups share their results with the class and a data table is created.
Explore
Define luminosity and brightness. Present the Inverse-Square Law. Ask the students to solve the equation for L. See discussion in overview. Do not, however, explain that the brightest stars are the farthest away. This is a part of our discovery process. With the class, write the luminosity equation for L 1 and for L 2. Then write the ratio. What disappears from the two equations? This is the equation that will be used. Sirius A will be L 1. Students will be given the distance to Sirius A and the brightness relationship between their star and Sirius A. Working in groups, they will find the luminosity relationship. Groups share their results with the class. Data is added to the chart begun on Day 2.
Summarize
Which star do you now know is the brightest of the stars you were assigned? Is it the closest star? What can you conclude? Why do you think this is true?
Homework
Provide the distance measurement and the brightness ratio of four stars. Students work as taught in class. Provide the brightness ratio and the luminosity ratio for a star and ask students to calculate the distance to the star. The reference star will be Sirius A for all these problems.

Comments: