Strategies
Within the different groups of word problems based on using proportions to solve, there are several different types of situations or categories of problems. There are problems with different difficulty levels and varying subjects. Because the students that I teach have a wide variety of needs, it is important to focus on the main weakness that all of the students tend to have: difficulty setting up proportions to solve word problems. This unit focuses on helping the student to work through several types of problems and correctly put them into proportions. The problems will be used to help the students develop an understanding of the goal of setting up proportions. The different subjects or situations in the word problems to make it possible to better relate to a diverse group of students. There are word problems that represent all different types of proportion problems.
The students will be taught exactly how a proportion problem is set up by using the units in the problem. Before that can be done, there will be a discussion about what the problem itself means. For example, let's say Joey went out of town to visit his grandma, which was a 120-mile journey. He traveled at the same speed for the whole trip. If it took him 2 hours to get there, what was his speed in miles per hour? There would need to be a discussion with the class about the problem itself. I would discuss with them what it means. If it took Joey two hours to get there, and he is traveling at the same rate, what kind of conclusions can we draw from that? Well, we could talk about if we figure out how far he goes in one hour, and then all we would have to do is multiply it by two to get what it would be for two hours.
After having the discussion about what the actual problem is asking, I will then lead the students to write a proportion. Writing a proportion allows a person to correctly solve a problem. The students will need to understand that the problem itself is discussing two different units; hours and miles. I would write that as a ratio, miles/hours. The ratio would be set up in front of the actual proportion so that the students could see where to place the miles and where to place the hours. The following proportion would need to be set up along with the ratio of units in the front:
miles/hours —> 120 miles/ 2 hrs = x miles/ 1 hr
There would then be a discussion about why it should be set up in that fashion. It is like an analogy; 120 miles is to 2 hours in the same way that x miles is to 1 hour. For the equation to make sense, both sides have to have the same units. The same units have to be on the top of the ratios, which is miles in this case, and the same units need to be on the bottom of the ratios, which is hours in this case. Having the students focus on where the units go is the main key. They should always label the numbers that they place in a proportion form so that they can check the units to be sure it is set up correctly. In this case it is miles on top and hours on the bottom. Some students may want to know while miles are on the top and hours are on the bottom. It is crucial for them to understand that it does not matter as long as the units are the same in the numerator and the units are the same in the denominator. That is, for the equation to make sense, both sides have to have the same units. I would show students that the answer would turn out the same if the units in the proportion above were flipped from numerator to denominator. As a class, we would discuss the similarities of the two proportions. The two ratios that make up a proportion are essentially unit rates, which I will go into more clearly below.
Unit rates
Unit rates are the basis of all proportion problems. Beginning with this topic allows the students to not only get an understanding of ratios and proportions, but they begin to see the importance of both units and unit rates. Students must have an understanding of unit rates for several reasons. First, they need to understand what a unit rate actually is. It is, for example how many miles a vehicle travels in one hour or how much it costs for one ounce of cereal, etc. The following set of problems will be used to introduce this topic. The proportions below each of the problems are the correct way to set them up.
A. Traveling cross-country, the Beeper family rode 510 miles in 8.5 hours. At this rate, how many miles did the Beepers drive per hour?
miles/hours —> 510 miles/ 8.5 hrs = x miles/ 1hr
B. Traveling cross-country, the Beeper family went an average of 60 miles per hour. If they traveled for 8.5 hours, how many total miles did they travel?
miles/hours —> x miles/ 8.5 hrs = 60 miles/1 hr
C. Traveling cross-country, the Beeper family went 510 miles at a speed of 60 miles per hour. How many hours did it take them?
miles/hours —> 510 miles/ x hrs = 60 miles/1 hr
The previous problems are all discussing the same situation. The only difference is in each problem a different variable needs to be solved for. Each of the problems are asking the students to look at the amount of miles driven, the amount of hours driven and the speed in miles per hour. Using these three different problems allows students to see the same type of problem could be set up several ways depending on the missing variable. The students will be able to see that in each of the proportions miles are on the top of the two ratios and hours are on the bottom of the ratios. The right side of the proportion represents the unit rate because the Beeper family drove 60 miles in one hour. I specifically chose a word problem that deals with miles per hour for a reason. My students never seem to understand that finding out how many miles per hour a car travels is a unit rate. Unit rates are individual rates of items. For example, if a problem states that a person is driving a certain distance and it takes them a given amount of time to get to a destination, finding the miles per hour would be the unit rate. I always need to stress with them that it is so many miles per one hour. The problems above are ones that I would do with my students. I would then give them problems to work on either individually or in pairs to ensure they can do it on their own. I would take these problems from the appendix. (See Appendix A, numbers 1-13 for additional sample problems based on unit rates.)
The first category that I dealt with was separating proportion problems into three different groups: unit rates, similar figures/scale drawings, and percents. Above I described how I would introduce unit rates to my students. Within unit rates, I determined another group. I constructed problems pertaining to the same topic, but with a different variable left out each time. This will give the students a variety of different ways to see the problems and also ways to set them up given different information. Again, one of the more difficult topics for students is to set up proportions correctly from word problems. This gives them practice in doing it several different ways.
Percents
Another category that I will introduce focuses on percents. Proportions that are set up with percents slightly differ from unit rates. Percents are used in students' lives every day. They see percents on their tests or report cards in the form of a grade. They go shopping and see discounts in stores that are a certain percentage off of the original price. The students will work with word problems that involve percents to set up proportions. Percent proportions are always set up the same way; with one of the ratios being a percent over 100. This is something that I stress to my students. The other ratio in the proportion needs to be set up in a certain way. The students need to look at it two different ways, depending on the type of problem they are working on as either is/of or part/whole. For example: There were eight equal pieces of pizza and Bobby ate two. What percent of the pizza did Bobby eat? As a class we would discuss the contents of the problem and figure out its meaning. If he ate 2 pieces out of the total 8 pieces, that would be one-fourth of the pizza. If we thought of one-fourth as a percent the answer would then be 25%. After understanding the problem, we would as a class come up with a way to set up a proportion. First, we need to identify what it is that is known in the problem. I see that Bobby ate 2 pieces out of the total 8 pieces of pizza. In this case it needs to be set up as a ratio in the form, part/whole. Focusing on the pizza as a whole broken into parts, I would set up the following proportion:
3 pieces (part) / 8 pieces (whole) = x % / 100
The proportion above is set up in so that the percent is the unknown. In the problem itself, it specifically asks what percent of pizza Bobby ate. Using the previous problem as a standard for solving other percent problems, the following examples would be given to the class.
D. There are 206 bones in the human body. There are 33 bones in the spinal column. To the nearest whole percent, what percent of your bones are in your spine?
33 bones (part) / 206 bones (whole) = x % / 100
E. There are 206 bones in the human body. About 16% of them are in the spinal column. About how many bones are in the spinal column?
x bones (part) / 206 bones (whole) = 16% / 100
F. About 16% of the total number of bones in your body are in you spinal column. If there are about 33 bones in the spinal column, about how many total bones are in the human body?
33 bones (part) / x bones (whole) = 16% / 100
The problems above are proportions that are set up with percents. All of the problems are similar in subject matter; they just differ with the variable that is missing. (To see more examples, see Appendix A, numbers 14 - 18.) Within this dimension of percent proportions, I have further broken the problems down. Above, I began by working with ones that were fairly simple, one-step problems that just had a different variable that was missing in each one. I will also vary the problems by making the problems a little more difficult by using complimentary percents and multi-step problems. Complimentary percents are a different type of percent problem. The question in the word problem is formed in such a way that it takes more than solving the proportion to complete the problem. There may be more steps included. For example, Amy went shopping and found a shirt that was on sale for 50% off. How much would the shirt be after the discount if the original price was $26? In this problem, the student is not just looking for the answer to the proportion; they need to take it to a higher level. If the students have the answer to the proportion, that would only tell me what the discount would be. In order to get the correct answer, the student would have to take the answer from solving the percent and subtract it from the original cost. That would then give the discounted price of the shirt. The following are examples of complimentary percents and/or multi-step percent problems.
G. Bob has a coupon for 15% off the price of any item in a sporting goods store. He wants to buy a pair of sneakers that are priced at $36.99. About how much will the sneakers cost after the discount?
x / $ 36.99 = 15% / 100 —> x = $5.55 —> $36.99 - $5.55 = $31.44
H. Lisa went to an electronics store that was going out of business. The sign on the door read "All items on sale for 60% off of the ticketed price." A computer has a price of $649, and a printer has a price of $199 and she needed both items. What was the total cost of the items after the discount?
$199 + $649 = $848 —> x / $ 848 = 60% / 100 —> $848 - $508.80 = $339.20
I. Between 1924 and 1998, the United States won a total of 161 medals in the Winter Olympic Games. If the United States won 59 silver and 42 bronze medals, about what percent of its medals were gold medals?
59 + 42 = 101 —> 161 - 101 = 60 —> 60 gold / 161 total = x% / 100 —> x ≈ 37%
Similar Figures and Scale Models/Drawings
The third main category that my problems are broken into is based around similar figures and scale drawings/models. This group works with setting up proportions in the way that the students learned with unit rates. It is important for students to understand the reasoning for keeping the same variables in the numerators, for example miles, as well as the same variables in the denominators, for example hours. The students will need to be sure to set up a ratio in the beginning labeling what goes on top and what goes on the bottom. They will also need to label all units on every number that they write into the proportions.
Similar figures and scale drawings/models are used in math and other subjects very regularly. In social studies, for example, students are given maps of different countries and cities around the world. The students need to be able to read the maps in order to understand them. Proportions give students an understanding of what a scale actually is. Scales are based on a scale factor. A shape may be stretched in every direction by a certain number or scale factor, which then makes the shape similar to the original. If I am trying to figure out how long it will take me to get somewhere, I use the scale to estimate the amount of time.
Similar figures are used regularly also. Whether it is enlarging or shrinking a picture or drawing blue prints for a new house, proportions are essential to figuring out the ratios. Similar figures are related by a scale change. If you know a length in one figure and the corresponding length in the other, their ratio is the scale figure. This factor then tells you the ratio of any pair of corresponding lengths in the two figures. The equality of the ratios of pairs of corresponding lengths gives a proportion.
The first step in solving the problems is to first draw a sketch. When dealing with similar figures or scale drawings/models, the problem for students is usually introducing two different figures. In order for students to see the correct way to set up a proportion, they need to be able to identify the corresponding sides. Corresponding sides of two shapes are ones that directly relate to each other. For example, if there are two similar triangles given, such as the ones below, identifying the sides that correspond to each other is key. The students would have to identify that the side that is marked 4cm on the first triangle corresponds to the side that is marked 6cm on the larger triangle.
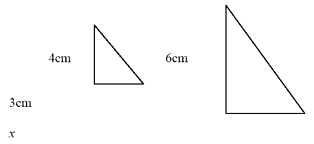
Looking at the two similar triangles there are a few observations that the students need to make and understand. First of all, the two triangles are the same shape but different sizes. That is what actually defines similar figures. Secondly, each side in the small triangle has a corresponding side in the larger triangle. With that information, a proportion can be set up. The ratio of any corresponding sides gives the scale factor. Therefore, the ratios between two pairs of corresponding sides are equal- they form a proportion. The base of the small triangle corresponds to the base of the large triangle and the height of the small triangle corresponds to the height of the large triangle. Therefore, the following proportion could be set up:
4 cm / 6 cm = 3 cm / x
Once the proportion itself is set up, the students should have no problem solving it. Within this category, I have broken the problems into several groups. There will be problems that deal with switching around the same variable in a given situation. For example if problem J below, you could be given the height of the Eiffel tower and not the height of the person. Once a student has an understanding of setting up proportions, it will be easier for them to switch variables around depending on what is given in the problem. Also, there will be problems that will be made more difficult through the use of fractions and decimals. In each of the problems the students will be expected to draw a picture in order to visually see the sides that correspond with each other. The proportion will then be set up based on the similar figures. The following are examples of either similar figure or scale drawing/model problems.
J. On a sunny day, the Eiffel Tower casts a shadow that is 328 feet long. A 6-foot-tall person standing next to the tower casts a 2-foot-long shadow. How tall is the Eiffel Tower?
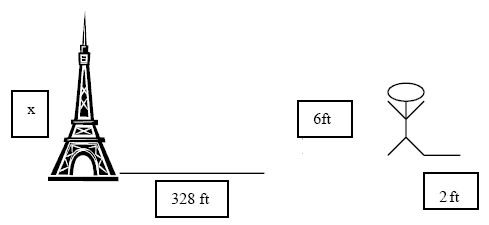
The following proportion would be set up to solve the missing height of the Eiffel Tower:
328 ft / 2 feet = x ft / 6 ft —> x = 984
K. Rachelle's school photo package includes one large photo and several smaller photos. The large photo is similar to the small photo. The small photo is 2 inches long and 1.5 inches wide. If the height of the large photo is 10 inches, what is the width?
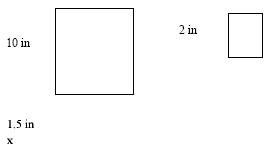
The following proportion would be set up to solve the problem:
10 in / 2 in = x in / 1.5 in —> x = 7.5
The two problems above show the exact process of how students would solve this type of problem. They would first have to sketch a drawing of the problem itself and label the lengths that they know. From there, the proportion could be set up. (See Appendix A, numbers 19 - 25 for additional problems.)
Solving proportions is a broad topic. With this unit, I have been able to analyze the types of problems and separate them into different groups in order to categorize them. The unit itself will allow students to have a much clearer picture of how to set up proportions from word problems. Having the students focus on all of the different dimensions will enable them to successfully solve proportion word problems.

Comments: