Urban Environmental Quality and Human Health: Conceiving a Sustainable Future

Strategies

I plan to use this unit at the very beginning of the school year/semester. It is a relatively short unit, probably only 3-4 days on a block schedule. I hope it will spark some interest, make my students aware of their environment and some social issues affecting it. I want them to think about alternatives with respect to things they do and things they eat. I also want them to recognize that math applies to other aspects of their lives, not just the math classroom. Dimensional Analysis is not typically taught formally in math classes, but it is a skill that got me through my engineering courses in college! I think that teaching it at the beginning of the course will serve as a good review of previously learned skills and get them thinking mathematically again. With respect to Delaware state standards, it addresses the content standards of Numeric Reasoning and Quantitative Reasoning, and the process standards of Communication and Connections.

My high school, in accordance with the school district, has instituted a Literacy Initiative for the upcoming school year for all grade levels and all departments in an effort to improve scores on the high-stakes DSTP (Delaware State Testing Program). As the initial part of my unit, I will develop "Before, During, and After" reading activities for daily articles that provide background information about pesticide use. These activities will not only satisfy the district and school Initiative, but also provide connections between mathematics and other disciplines. Also, by starting the school year with a reading assignment, my students will learn right from the start that they will have to read and process their reading, even in math class.

I've referred to Dimensional Analysis, also known as the Factor-Label Method ¹², several times already. It is a method for keeping track of units in calculations, and is particularly useful when working with complicated formulas. If the units come out "right," then the answer is probably right, too. If data is provided in units other than those needed in a formula, it can be converted to appropriate units by Dimensional Analysis. The underlying mathematic principle is the Identity Property of Multiplication, namely that the value of a number does not change if it is multiplied by the number one. From our knowledge of fractions (said with tongue in cheek, since many students are terrified of fractions), if the numerator and denominator of a fraction are equal, then the fraction is equal to the number one (i.e. 5/5=1). So, if we want to convert units, and we know the conversion factor, we make a fraction equal to one by strategically putting one part of the conversion factor on the top of the fraction (units and all) and the other part in the bottom. We multiply or divide units as we would multiply or divide numbers or variables, and look for and "cancel" values of one. For example, to convert 6 inches to centimeters, we need to know a conversion factor such as 1 in. = 2.54 cm. The calculation, using Dimensional Analysis, is 6inx2.54cm/1in=15.24cm. What I meant, above, by "strategically" arranging the conversion factor is that since 2.54cm/1in=1in/2.54cm=1 , I chose the fraction so that the units I started with (in.) would cancel with the same units in the denominator (in./in.=1), leaving the desired units cm in the numerator. Once we check that the units will work out the way we want, we perform the mathematical operation 6 ´ 2.54 = 15.24 and attach the remaining units to our result. If the problem were to convert from 10cm to inches, we would use the fraction with 1in. in the numerator and 2.54cm in the denominator (10cmx1in./2.54cm) so that cm would cancel and leave only inches as the final units. Then we would compute 6/2.54 = 2.4 because the value 2.54 was in the denominator. This process is also called the Factor-Label Method because you are multiplying (factors) labels and looking at how to set up the equations to cancel the unit labels. It is also possible to do multiple conversions in one calculation. For example, to convert 500cm to yards, I would set it up as 500cmx1in./2.54cmx1ft./12in.x1yd./3ft. Notice that each fraction is equal to one. (Of course, I could have used 1 yd. = 36 in. in place of the 2 ^nd and 3 ^rd factors in the expression above.) First the cm cancel, leaving you with in. Then in. cancel, leaving you with ft., and finally ft. cancel, leaving you with yd., the desired units. When the conversions are set up this way, students can easily see that they need to start with the number 500 and divide it by each of the other numbers. Warning: I have seen students try to type the division steps in all at once and do it incorrectly. For example, if they type 500/2.54x12x3, their product will be incorrect because they would be multiplying by the 12 and 3 rather than dividing. Hopefully, writing out the 3 conversion factors as fractions they will recognize that they must divide three times to convert from cm to yd.

In this unit, pesticide exposures are often given in mg (micrograms, or one-millionth of a gram). Since most students won't have a good feel for metric measurements, I will have them convert to something more familiar: ounces. The most commonly known conversion factor for converting metric mass to English weight units is 1kg = 2.2lb., and then 1lb. = 16oz. It's also helpful to know the metric prefixes, and 1g = 10 ⁶mg. So, if the maximum residue level is 2.3mg, we could set up the calculation with multiple factors, as 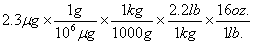. The mg, g, kg, and lb. units will all cancel, leaving oz., as desired. The mathematical calculation is then 2.3/10^6/1000x2.2x16 = 8.1´10^-9. I know that this calculation will trigger the additional discussion with my students of what the "E ^-9" means on their calculator screens. They have all been exposed to Scientific Notation in previous math and science classes, but it never hurts to reinforce its meaning and purpose.

At this point, another follow-up to the conversion of mg to ounces will be the concept of ppm (parts per million) or ppb (parts per billion). It's another example of Numeric Reasoning. The result above, 8.1´10^-9, represents the very small number 0.0000000081, which can be written as the fraction 8.1/1,000,000,000. Since the denominator is the number 1 billion, 8.1´10^-9 is equal to 8.1 ppb. When I have students working with very large or very small numbers like these, I like to help them put them into perspective. So, once again, I will integrate a Literacy strategy of reading aloud to students, interjecting comments as I read. One children's book that I like, How Much is a Million, by David Schwartz, actually states the assumptions used make the analogies for millions and billions of items, so my students can practice Dimensional Analysis computations to confirm the calculations in the book.

Now that the students have regained their math skills, it's time to return to the topic of pesticides. I want students to consider how they are exposed to pesticides, and at what level. I want them to consider their diet, as well as their actions (indoor/outdoor activities, use of pesticides indoors/outdoors, etc.) There are several documents published by the U.S. Government that I will make available on the school computer network's public drive to have students calculate exposure levels to pesticides. First is the EPA's Child-Specific Exposure Factors Handbook (Interim Report), and second is the USDA's Pesticide Data Program Annual Summary, Calendar Year 2006. I will also upload several files with chlorpyrifos exposure data that was submitted to EPA for reregistration of the pesticide.

The 1996 FQPA forced more government groups to focus on potential risks to children. The Child-Specific Exposure Factors Handbook has data extracted from the full EPA Exposure Factors Handbook for adults and children. The child-specific factors include factors that affect children from birth through age 19 years, just perfect for high school students. All routes of pesticide exposure are considered, beginning with ingestion of food and water. There are separate chapters devoted to Breast Milk Intake, Food Intake broken down into categories such as vegetables, grains, fruits, milk, and meat/fish. The chapter on Drinking Water Intake includes direct and indirect (added during food preparation) water use. The handbook even provides data for amounts of Soil Ingestion and Nondietary Ingestion (primarily from hand-to-mouth action by young children). The second type of exposure considered is Inhalation Routes (varies with activity level), and finally Dermal Routes, taking into account the surface area of young children versus older ones. The chapter entitled Activity Factors may apply to any of the three exposure routes. Each chapter describes the studies that produced the data and even states a low, medium or high confidence level for the data provided. Fortunately, the data is presented in a multitude of tables, and you can find a list of tables early in the document.

The Pesticide Data Program Annual Summary, Calendar Year 2006 gives numerical values for pesticide residues on foods and in water. The data covers fruits and vegetables, peanut butter, wheat, poultry, and bottled and municipal drinking water. It also gives information about foods that have multiple pesticides and/or residues. I learned that there can be more than one residue for a single pesticide if it metabolizes or degrades into a different chemical compound. The narrative of the report explains the sampling and laboratory methods used. But, the most useful data in the summary report for this unit is the levels of specific pesticides on specific foods, which is compared directly to the EPA tolerance levels in the same table. I want my students to spend some time with some of the data tables and the narrative that explains how the numbers were derived. This kind of activity is another one of those skills that we don't typically teach directly. But, here is a perfect opportunity for students to experience some real data that applies to them. In addition, interpreting tables and graphs is part of the state standards in all content areas. By preparing a set of questions, I will again satisfy our literacy Initiative and ensure that my students understand the data. I also hope it will generate some excited and constructive discussion in the classroom.

Another significant document in the study of pesticides is the 2006 Update of the Organophosphate Cumulative Risk Assessment published by the EPA. It combines pesticide exposures from a variety of sources and exposure routes for varying age groups (young children, again, being of primary concern because of the FQPA) to make sure overall exposure levels for each pesticide meet the EPA tolerances. This Cumulative Risk Assessment relied on the data from the USDA Pesticide Data Project described above. It is an enormous document full of a lot of statistical justification for the pesticide levels that are stated. However, by plodding through it, I found some items that I would want to share with my students. For example, pest strips and flea collars contribute a large piece of the inhalation exposure route for pesticides in residential scenarios because they continually release the pesticide until it's gone after several months. ¹³ The document also lists the foods consumed by different age groups in decreasing order of consumption. It also states the foods in the top 0.2% for organophosphate residue. In other words, these foods (snap beans, watermelon, and tomatoes are the top three) have more residue than 99.8% of all foods. ¹⁴ Something else that I learned from this document is a long list of acronyms (I suggest you keep a running list if you decide to attack the document), which I have included in Appendix B. And, my big "Ah-hah" after several days at it was that in order to add all types of pesticide exposures together (multiple chemicals with different toxicity levels plus multiple exposure routes), you have to make the data compatible. It's kind of like finding a common denominator before adding fractions. In the pesticide world, you need to find relative toxicity. EPA has a way to do this: they find a Relative Potency Factor (RPF) based on one pesticide that they have a sufficient amount of data for. Then, all other pesticides are compared by ratio to the reference one. Doing the comparisons and interpreting the data is another potential mathematics exercise for students. Also, there are some exponential equations that appear for modeling the effect of different organophosphates on cholinesterase activity. These equations, along with half-life information, could be used in upper level math courses in the study of logarithms.

Now it's time to blend pesticide data with Dimensional Analysis. To keep things relatively simple for this unit, I will focus on EPA data and tolerances for chlorpyrifos, although, I will encourage my students to research EPA data for some other pesticides that they may be familiar with and for alternatives that pose less risk. Going back to the question about the pesticide residue on an apple from the opening of this unit, I will demonstrate how to calculate the amount of residue on an apple as if it had the maximum ("worst-case") reported level of chlorpyrifos and compare it to the corresponding EPA tolerance level. The maximum reported chlorpyrifos residue on an apple was 0.4 ppm. ¹⁵ Hopefully I will be able to procure a balance from the science department so we can find the mass of the apple in front of them. If not, we'll estimate that a medium-sized apple has a mass of approximately 150g. Then the mass of chlorpyrifos of 0.4 ppm by weight would be 0.4/1,000,000x150g=60g/1,000,000, or 6´10^-5g. This small number could be converted to milligrams by 6x10^-5gx1000mg/1g=0.06mg, and could have been done all in one equation. The EPA tolerance for acute exposure to chlorpyrifos is 0.0017 mg/kg-day. ¹⁶ The units mg/kg-day means milligrams of chlorpyrifos per kilogram of body weight per day. Therefore, students need to determine their own body weight in kilograms, using the conversion factor for pounds to kg given above. A petite student that weighs 110lb. would have a mass of 110lb.x1kg/2.2lb.=50kg. This student's tolerance level for chlorpyrifos exposure for one day would then be 0.0017mg/kg/dayx50kgx1day=0.085mg. Since the residue level on the apple (0.06mg) is less than the tolerance level (0.085mg) for this person, the apple should not pose a risk. I would have all students calculate their own exposure tolerance for chlorpyrifos and compare their results to others'. This comparison should help them understand why young children are at a greater risk of pesticide exposure than adults, especially if I have the largest and smallest student in the class stand side by side and report their exposure limits!

Sample inhalation and dermal exposure calculations for dog collars containing chlorpyrifos, based on EPA data from the "Residential" file are next. Adults' inhalation and dermal exposures are reported as 0.74 mg/kg body wt./day and 0.045 mg/kg body wt./day, respectively. ¹⁷ For a male high school student (we're assuming he fits the adult category) that weighs 145 pounds and spends 3 hours a day in the same room with his dog, his inhalation exposure would be calculated as 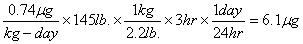. If the same student spent 20 minutes a day petting his dog, his dermal exposure would be . 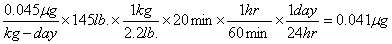The maximum exposure limit for a 145 lb. student would be 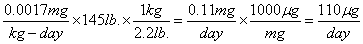. Combining the inhalation and dermal exposure to the student's dog in one day (6.1mg + 0.041mg = 6.1041mg), he is well below the limit for chlorpyrifos exposure (110mg). And again, I would reinforce the differences in the exposure numbers for the largest and smallest student in the classroom.

These are basic examples of using ingestion, inhalation and dermal exposure data to estimate the risk of exposure to chlorpyrifos. There are a multitude of computations that can be done with the information provided in governmental publications and other online resources. For example, Geometry topics, such as surface area and volume, can be embedded in the calculations. Science topics, such as density and concentration, can be included. In addition to the Mathematics topic of logarithms I mentioned earlier, this data could also be used in Statistics units. Refer to the lesson plans in the Classroom Activities section, and Problem Sets in the Appendix for additional resources for mathematical calculations relating to pesticide exposure.