Energy, Environment, and Health

4. Lesson Plans

Lesson plans are divided in two categories, according to the level of difficulty. One level is directed to Algebra-1 students, with applications of linear functions and systems of equations. The manipulation of variables in some formulas is also included. The lessons for Algebra-1 can be easily adjusted for a 7 ^th and 8 ^th grade math classes as well as a Geometry class, given that the word problems involve area and volume.

The second category is devoted to Algebra-2 and they could be used as well in Pre-Calculus and Trigonometry/Math Analysis. This second category includes lessons using linear, quadratic, rational and exponential functions. Graphing is a very important skill to master in order to continue to more advanced math classes; therefore, the interpretation of a graph in a real life situation is also very important to master. The word problems chosen to illustrate one of the aspects of pollution include Mathematical Reasoning, which is mentioned in the Common Core Standards for High School Math. ⁴

Lesson Plan-1: Introduction of Curriculum Unit

Math Level: Algebra-1 & Algebra-2

Content Standards: California Content standards 5, 7, 9, and 16 are addressed in this lesson. These standards are related to solving word problems with equations, graphing lines and linear functions. ^4a

Learning Goals: Relating the danger of pollution, health complications, fracking and the consumption energy.

Prior Learning & Anticipatory Set

Students are familiar with the rising prices of gasoline, but are not aware of the extraction process and the pollution created as a collateral damage. Students will be in groups of 4.

Instructional Strategies

Warm-up for 5 to 10 minutes introducing new vocabulary used in the context of pollution.

A video called "Pollution for Morality" ⁵ will be shown in class for 4 minutes.

Group Work

Discussion about the consequences of pollution will be done within their groups for 5 to 10 minutes. Groups need to come up with 2 main ideas that they noticed were damaging the environment and 2 ideas on how can they quantify the damage. In other words, how can they use math to find the magnitude of the damage.

Sharing / Assessment

Groups will prepare a poster indicating their 2 main ideas about the information seen on the video and their 2 ideas on how can they use math to measure the problem.

Closure

In a video that is about 3:33 minutes in length, CNN explains what fracking is. The remaining of the time will be devoted to discuss the video. ⁶

Vocabulary (Language Objective for English Learners)

A list of unknown words will be created to help students understand the lesson. For instance, the words "Carcinogen," "Shale," and the phrase "Hydraulic Fracturing" are good examples of the new vocabulary.

Lesson Plan-2

Math Level: Algebra-1 & Algebra-2

Content Standards: California Content standards 5, 7, 9, and 16. These standards are related to solving word problems with equations, graphing lines and linear functions. ⁴

Learning Goals: At the end of this lesson students will be able to analyze and solve word problems applying algebraic concepts of linear functions in a real life situation, as well as to calculate volume as a function of the variable radius, with a constant thickness.

Prior Learning & Anticipatory set

Students are familiar with working with variables and formulas as well as the concepts of functions and solving equations and, what they have heard in the news about oil spill. They will be in groups of 4.

Instructional Strategies:

Warm-up for 5 to 8 minutes with review of prior learning experiences, such as solving equations, calculation of volume of a cylinder and linear functions.

"Marine Pollution" video will be presented for 4:29 minutes ^5a showing the real life problem.

After the video, I will devote 5 minutes for comments and questions as whole class.

After the comments, a real life problem will be given to each group. The problem is the same, but the numbers may be different at the discretion of the teacher. This activity will take 10 to 12 minutes.

The problem: Oil Pollution

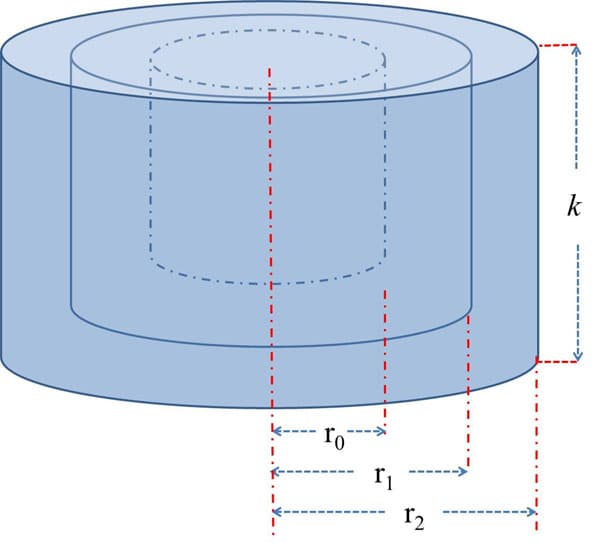
An oil slick spreads evenly in the ocean, in all directions from a ruptured tube (the central point) and it tends to be circular with a radius "y," which changes constantly as a linear function of time. The thickness of the slick is a constant k = 0.023 meters. The radius of the slick after 1 day is 140 meters and after 2 days is 260 meters.

Question-1: What would be the volume of the slick after one week?

Question-2: What is the radius of the ruptured tube?

Solution

A linear function can be written as the model y = mx + b, where y represents the radius of the slick and x represents the time in days.

The information given provides two points (1, 140) and (2, 260), which are going to be substituted in the linear function model to obtain a system of two equations as follows:

y = mx + b

260 = m (2) + b

140 = m (1) + b

After solving the system of equations, it is obtained that m = 120 and b = 20; therefore the linear function is y = 120x + 20

To answer question 1, the number of days would be x = 7. With this value we can find the radius y and, therefore, the volume of the slick after 7 days, using the formula for the volume of a cylinder V = 0.023?? r ²

The radius is y = 120 (7) + 20. After simplifying, y = 860 meters. This result will be substituted as follows:

V = 0.023 (3.14)(860) ²

V = 53,413.912 m ³

To answer question 2, the constant b from the linear function represents the y-intercept of the line, which is the starting value of the radius of the slick. As a consequence, the radius of the tube would be 20 meters.

Closure

Each group will share on a poster, how they found their answer. If the problems have different numbers, it would allow finding a pattern in the solution of the problem. If the numbers are the same we can focus in looking at the different ways students approached the problem. Also, discussions about the consequences on the environment where the slick happened and similarities to the already well known cases of oil spill.

Vocabulary (Language Objective for English Learners)

Examples of words that might be new for English Learners are, slick, thickness, ruptured,

Lesson Plan-3

For this lesson, the approach would be exactly the same as lesson plan-2, but it will be directed to Algebra-2 and Pre-calculus students.

The problem: Oil Pollution

An oil slick spreads evenly in the ocean, in all directions from a ruptured tube (the central point) and it tends to be circular with a radius "y," which changes constantly as a quadratic function of time. The thickness of the slick is a constant k = 0.023 meters. The radius of the slick after 1 hour is 15 meters, after 2 hours is 24 meters and after 3 hours is 37 m.

Question-1: What would be the volume of the slick after 10 hours?

Question-2: What is the radius of the ruptured tube?

Answers: V = 4,159.87 m ³ and radius r = 10m

The above problem can also be adjusted to use exponential equations instead of a quadratic model.

Lesson Plan-4

Math Level: Algebra-2 / Pre-Calculus

Content Standards: California Content standard 12 and 15. These standards are related to solving word problems with exponential functions. ⁷

Learning Goals: At the end of this lesson students will be able to analyze data given with a graph, applying algebraic concepts of exponential and quadratic functions in a real life situation.

Prior Learning & Anticipatory set

Students are familiar with exponential and quadratic models, solving equations involving one of these concepts. They will be in groups of 4.

Instructional Strategies:

Warm-up for 5 to 8 minutes with review of prior learning experiences, such as solving equations with a model and points that belong to the given model.

"CNG Conversion" video will be presented for 5 to 15 minutes ⁸ showing how the process works.

After the video, I will devote 5 minutes for comments and questions as whole class.

After the comments, a real life problem will be given to the groups. This activity will take 10 to 15 minutes.

The problem:

The number of natural gas converted vehicles between 2001 and 2010 is illustrated in the graph below. Blue color bars represent the projected outcome and the red bars represent the actual numbers. The graph uses curved blue and red trends to show the graph of the model.

Write the equation of best fit of the graph obtained with the actual numbers (red trend), knowing that it is of the form y = a?b ^kx

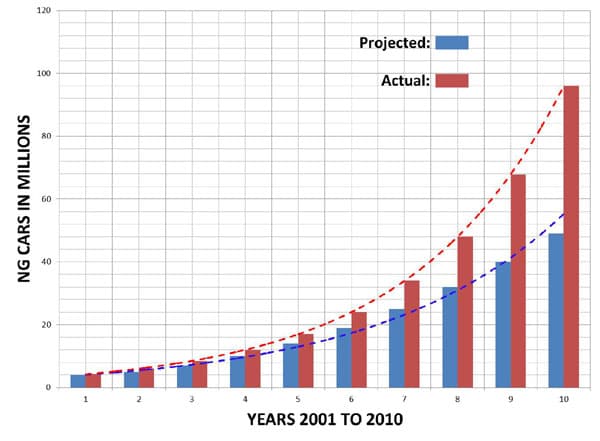
Answer: One of the possible models is y = 3 x 2 ^0.5x

Closure

Groups will compare their equations. Equations may differ, but should have similar numbers.

Language Objective for EL students

Projected vs. Actual, Acronyms CNG, NG,

Additional Problem

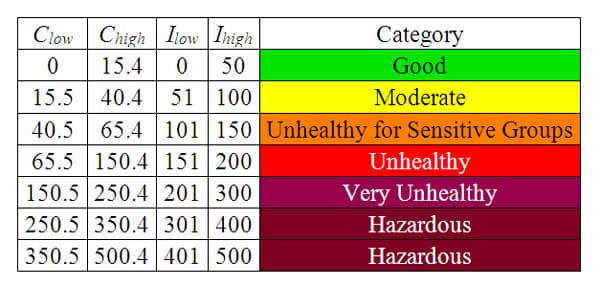
The average concentration of fine particles PM _2.5 is recorded in a monitor for a 24-hour period. The reading of the concentration on the monitor is 20.5 micrograms per cubic meter. What is the AQI? The table of breakpoints for PM _2.5 is given below.

Solution

The value of the concentration "C" is 20.5, which is between 15.5 and 40.4. These two last numbers are the C _low and the C _high in the formula to calculate the AQI. The values of I _low and I _high are the corresponding numbers in the table.

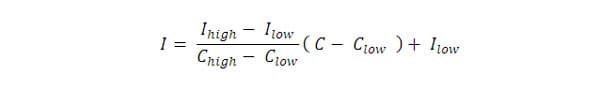
I = (100 – 51)x(20.5 – 15.5)/(40.4 – 15.5) + 51

I = 60.84

For this problem, the result of the AQI of 60.84 is under the yellow range, which is considered "moderate." The table appears above in section 2.4.