Classroom Activities
My curriculum unit will focus on helping students improve their proportional reasoning thereby laying the groundwork for more successful high school math and science experiences. The unit can be used as a “Unit 0” to start the year in any high school math class. Since it is for high school, it will assume elementary understanding of number lines and fractions and work toward bringing the pieces of previous knowledge students bring with them into a cohesive whole.
The Number Line
The unit will begin by defining the number line. I anticipate that many of my students will not need any scaffolding or additional instruction on the number line, but I will plan for supplemental activities/instruction to be used as needed to ensure that all students begin with a solid understanding of number line basics.
Activity 1 (2 Days)
I will begin with instruction that defines number line and related terms. I will emphasize that numbers represented on the number line represent both distance and direction. My goal is for students to understand that the whole numbers 1 and -1 are exactly one unit from the origin (zero). Each whole number is placed a distance from zero that is a multiple of the established unit. After students understand the definition of the number line, each student will use a straight edge and a blank piece of paper to create a number line with numbers from -3 to 3.
As students work, I will move through the room asking individual students questions as needed. Once all students have completed their number line, I will ask whole class questions with the goal of guiding the students to improve their understanding of values of numbers, fraction placement, and fraction comparison. The discussion will guide which questions I ask. Possible questions include:
- Is positive 2 greater than or less than negative 3? How do you know?
- How does negative 1 compare to 0?
- How many units from 0 is negative 2? Positive 3? Positive 1? Negative 3? What do you notice about your answers?
- Where would you place 1⁄2? How did you know where to place it?
- Where would you place 1⁄4? 1⁄8? 1⁄16?
- Where would you place 1⁄3? 2⁄3? 3⁄3? 4⁄3? 5⁄3? 6⁄3?
Once students have built a number line and placed an assortment of fractions on the number line, students will work in pairs to add fraction sets to 8 different number lines. Each pair of students will be given a set of number lines to work with. See Figures 12a and 12b. Students will work together to mark each number line from 3 to 4 with all the fractions which have denominators of 2, 3, 4, 5, 6, 8, and 10.

Figure 12a: Side 1 of Activity 1 Student Handout. This handout should be printed on 11x17 paper.
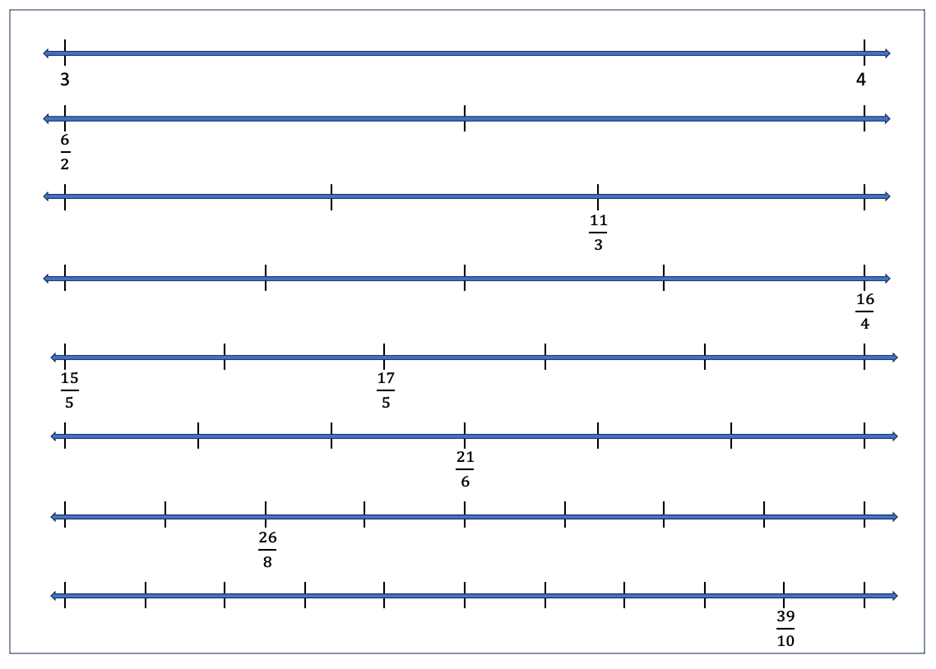
Figure 12b: Side 2 of Activity 1 Student Handout
Again, while students work, I will move through the room asking student pairs questions as needed. Once most pairs have completed their number line, I will ask whole class questions with the goal of guiding the students to improve their understanding of values of numbers, fraction placement, and fraction comparison. The discussion will guide which questions I ask. Possible questions include:
- Is 22⁄6 less than or greater than 20⁄6? How do you know?
- Is 3⁄7 less than or greater than 5⁄7? How do you know?
- Is 18⁄5 less than or greater than 7⁄2? How do you know?
- Is 3⁄5 less than or greater than 1⁄2? How do you know?
- Is 7⁄2 less than or greater than 21⁄6? How do you know?
- What other fractions are equivalent to 7⁄2?
- What is another fraction equivalent to 7⁄2 that is not on our paper? How did you think about that? What is a different way to think about that?
- Is 10⁄3 less than or greater than 18⁄5? How do you know?
- Is 1⁄3less than or greater than 3⁄5? How do you know?
- What if you didn’t have these number lines to look at? How would you compare 5⁄12 and 4⁄17?
What I want my students to demonstrate at the end of this activity is a clear understanding of the magnitude of positive and negative numbers. Do my students understand that it is the placement on the number line that determines which number in a pair has greater numerical value. Is it clear that distance from zero is one concept and relative value is a different concept? Do my students recognize equivalent fractions? Do my students understand the impact the size of the denominator and the numerator have on the size of a fraction?
Activity 2 (1 day)
With our newly improved number sense because of our recent number line work, we will explore addition and subtraction using the number line. Students will be given a handout with 10 number lines numbered from -5 to 5 on one side of their handout and 10 number lines numbered 0 to 1 including various fractions represented on the other side. We will begin by recalling how arrows represent the distance and direction of numbers on the number line.
The initial work will be done whole class guided by slides. See Figure 7a for an example. The first slide would show the first number line in Figure 7a. It would be followed by a slide showing the second number line in Figure 7a. I anticipate it will take 5 to 8 problems for all students to be comfortable representing whole number addition and subtraction on the number line. In each class, I will present as many problems as needed before moving on to working with fractions.
Possible expressions I could ask students to represent/solve include:
- -3 + 2
- 1 + 4
- 4 + 1
- 0 + 3
- 5 + (-2)
- (-2) + 5
- (-2) + (-3)
- 2 - (-3)
- (-3) - 2
- 1 - (-4)
As we move to adding and subtracting fractions, I will start with common denominators and then move to expressions with different denominators. Students will need to think about the fractions and mark their number lines accordingly if the needed partitions are not represented. Several 0 to 1 number lines with no fractions will be provided giving students different options for how they approach solving these expressions. The primary goal of working with fractions in this context is for my students to deepen their conceptual understanding of equivalent fractions.
Possible expressions I could ask students to represent/solve include:
Proportional Reasoning
Once we have completed our number line work, I will introduce proportional reasoning with a thinking task. Students will be randomly assigned to groups of 3. Students will stand with their group and gather around a rolling whiteboard in the center of the room. I will introduce the following problem which is adapted from Teaching Fractions.18
Activity 3 (1 day)
Problem: There are two large pitchers which contain tropical punch flavored Kool-Aid. Each pitcher of Kool-Aid has been made by mixing powdered Kool-Aid flavoring with water. The powdered Kool-Aid comes with a standard size scoop. One pitcher is made with 4 scoops of Kool-Aid mix and 2 gallons of water. The other pitcher is made with 4 scoops of mix and 3 gallons of water. Students are asked to compare the Kool-Aid in the two pitchers.
Questions include: Will one of the drinks have a stronger tropical punch taste? How could you measure the “punchiness” of any Kool-Aid mixture made with the powdered Kool-Aid flavoring and water? Does it matter that one of the pitchers has more liquid in it than the other one does? Why or why not? Suppose you obtained 3 measures from 3 different pitchers whose powdered mix to water ratio were 3 scoops of powdered Kool-Aid to 4 gallons of water, 3 scoops to 5 gallons, and 3 scoops to 2 gallons. How would you use these numbers to rank the mixtures from the weakest to strongest tropical punch taste?
I present the entire problem stopping to draw pictures of the pitchers to provide students with a visual. I will write each question on the board as well. I will ask a student to sum up the facts as a check that students understand the general problem. Then the students are sent to find a space at the whiteboards around the classroom to work on the problem. I do not answer questions until students have had time to work. And as part of the class norm we establish for this type of task, I will not confirm or deny whether students have arrived at a correct answer. I will not directly answer questions about what to do next or how to start. I will answer almost every question a student has by either referring them back to the illustration on the whiteboard that I drew or by asking the student a question to help them move forward.
When I release the students to start working, I task them with answering just the first question. Once a group is confident in their answer to the first question and can explain their “why”, the group will move forward to the more general question of how to measure “punchiness” of any given mixture.
As the groups dive into the problem, I anticipate most students will recognize which pitcher has the strongest taste. By asking how to measure the “punchiness” students will have to think about an answer that is not dependent on the numbers in a specific situation. They will have to generalize what they know about a specific situation. Students will also have to think about what happens to the taste as you add more water or less water.
We will come together as a group to debrief before the end of class.
Activity 4 (3 to 4 days)
The remainder of our time in this unit will be working word problem sets. We will work with selected problems and problems adapted from Teaching Fractions. Students will work with their groups. I will move through the room pushing in as needed. At the end of each class we will come together and share our problem solving strategies.
I will use 3 different sets of word problems. The first set will be proportion problems which do not include numbers. I believe the advantage of using word problems without numbers is that it allows students to not be distracted by the urge to get a final answer. So many of my students approach word problems by pulling out all the numbers they see, adding operations, and hoping for the best. This first set of problems will give students a chance to think about what proportions are and to focus on recognizing the units. Example problems of this type can be found in Teaching Fractions.19
I will supply numbers for the second set of problems. We will begin with 2 or 3 of the problems from the first set to allow students to see the “next step” in solving problems they have already spent time with. Then we will move to a group of problems in two distinct sets. Each set will be similar problems that are each slightly different. The first set of problems will be related to unit conversions. My students struggle with unit conversions. This struggle impacts their success in both math and science. The second set of problems will be related to interest rates. I believe the real-world application of interest rates will help prepare my students for the adult world of credit cards (and what a bad deal they are!) as well as help them to understand car loans and how compound interest works. Ideas for problems of this type can also be found in Teaching Fractions.20
For the final set of problems, I will work with examples of more challenging problems from Teaching Fractions.21 The first two problem sets will include 20 problems each. This final set of problems will contain 3 to 5 problems designed to work like our thinking problems. Depending on how students are progressing I may choose one problem and spend a class period working it with our Thinking Tasks protocol. Then I will introduce a set of 3 challenging problems as group work the next day.

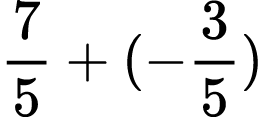
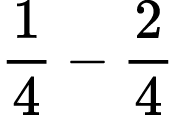
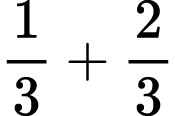
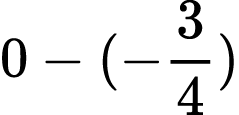
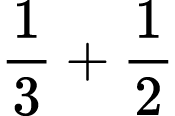
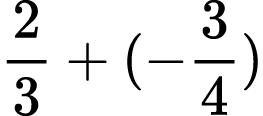
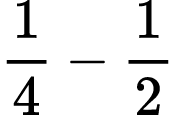
Comments: