Overview
Based on my fourteen years of teaching Algebra to 7th and 8th graders in public middle schools in Oakland and Berkeley, I can confidently say that word problems are the part of the subject that is least liked by the students. Whenever word problems are introduced, many of my students react the same way: blank faces and groans. It feels as if a massive impenetrable steel wall separates my students from engaging with word problems. Many students shut down and literally say “I don’t do word problems”. Their avoidance of taking on the challenge and the reflexive belief of their inability of solving word problems are present at all skill levels. Neither good number sense, nor flexibility with number relationships exempts students from having negative views on word problems. Their apprehension does not dissipate as they enter higher math classes. In fact, many high school teachers in Algebra 2 and Calculus notice similar misgivings from their students. Thus elementary and middle school teachers have an important responsibility to teach students to feel more comfortable and gain confidence with solving word problems.
Another major concept that my 8th graders struggle with is solving multi-step linear equations.
Many of them lack the conceptual understanding from previous grade standards. Many students do not have a clear understanding of the many facets of variables. They lack a formal understanding of the Rules of Arithmetic, which interferes with simplifying expressions. They also lack a robust understanding of equality and equivalence. The combination of this confusion and misunderstanding comes to the surface in many different ways, expected and unexpected, when they are faced with multi-step one variable equations.
The purpose of this curricular unit is to improve my students’ performance in solving linear equations and word problems by teaching the two topics simultaneously so that they can have a more positive and successful experience in high school math classes. This unit works to fully engage students from different cultures and levels of skill, using word problems to flush out and address the many misconceptions and gaps in prerequisite skills and at the same time to help students construct deep conceptual understanding of the procedures of algebra. The focus of the unit is on helping students realize the efficiency of using algebraic equations as they work through progressively more complex word problems using both an arithmetic approach and a procedural algebra approach. It is expected that their reliance on computational strategies will gradually transition to using procedural algebraic problem-solving strategies as problems increase in complexity and as they notice the limitations and benefits of both approaches. Furthermore I hope that facility with both approaches will deepen their understanding of algebra. Moreover I want my students to become flexible problem solvers, which means they can modify their approach when faced with challenges during the problem-solving process. In other words, they can start with an algebraic procedure then switch to an arithmetic approach if they realize their initial approach is too cumbersome or vice versa. Thus, they will effectively learn more about both approaches.
Scope and Sequence of Linear Expressions and Equations
This unit is the last of the four interrelated units developed in 2017 Yale National Initiative (YNI) Math Seminar. Due to the breadth and importance of learning to solve word problems with symbolic algebra, four national Fellows (2017 math Fellows Rachelle Soroten, Jeffrey Rossiter, Xiomara Pacheco, and I) built separate but related curricular units, for each section with word problems as the underlying theme. The first unit covers translating simple one-step and two-step word problems into equations. The second unit delves into translating complex phrases into expressions with many more terms in preparation for deriving multi-step equations. The third unit uses properties of the operation to simplify expressions. This fourth unit focuses on solving equations starting with one–step equations, going up to multi-step equations including variables on both sides of the equal sign. Below is a graphic that shows the scope and sequence of the four curricular units.
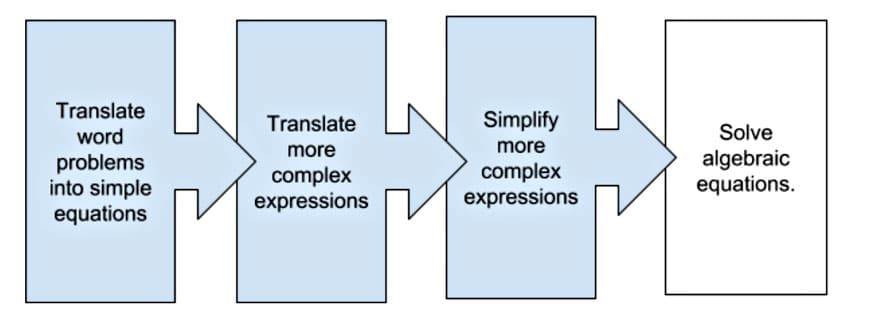

Comments: