The Mathematics of Wallpaper

Content Objectives

The Number Line

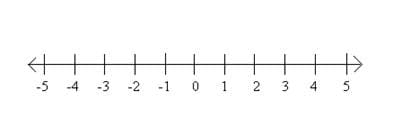
This is a number line. The number line provides a model for explaining the four basic operations for all rational numbers. It is by nature a spatial object: a set of points one can pass through as a journey along a path (Ryan, 2007). Use of the number line allows the student to "situate themselves bodily and spatially in the mathematics in a powerful way (Lakoff and Nunez in Ryan, 2007). It is actions+gestures+words (Ryan, 2007); a dependence on our visual-spatial skills that permits us to conceptualize mathematically the world around us. The numbers on the number line represent a number of units of length. Specifically, a given number on the number line tells the distance between the point that it labels and the origin. This means that the distance between any two points is given by the difference of the numbers labeling those points. 0 represents the point of origin and there are numbers on either side of it; numbers to the left of 0 are called negative numbers. Thus, the sign of a number labeling a point tells you the direction to go from the origin. We call the combination of the direction and length the oriented distance of the point from the origin Number lines can also be combined so that one is horizontal and it is intersected at 0 by a vertical line, and then you have a grid which is called the Cartesian coordinate system. The number line is considered to go on forever on either direction. If it didn't, it would be called the number line segment!

When I began to plan a unit on symmetry, I would never have thought to focus on the number line and multiplication. I kept asking myself, "What does this have to do with symmetry??" But then I found out! The number line, this seemingly simple tool—although it is really quite sophisticated–is foundational for interpreting math geometrically; moving one space—a translation by one unit, which is addition of 1 on the number line is a key part of understanding the symmetry of patterns. We see the beauty of symmetry all around us: in the fabrics we wear, in art (M.C. Escher), architecture (Moorish tiling) and nature (flowers, a beehive). Mesmerized by the beauty of these things, one rarely stops to consider the mathematics that gives rise to it. Doing one thing and then another to a geometric shape is a mathematical operation. Hence, symmetry is infinitely mathematical, therefore to truly understand it; one must first know the mathematics that gives rise to it.

My first job is to determine if my students understand what a number line is and how it works. Even though this particular unit is about multiplication and division, it is worth taking the time to talk to students about how a number line potentially goes on forever, that 0 is called the origin—it has an important place on the line: that all distances are measured from here- and that the units can be broken down into even smaller units. The most important concept about the number line though, is that it shows distance. For example, I will call two students to the front of the classroom and place them some distance apart. Then I will ask another student to come forward and measure off in steps how far apart the two students are. He might say something such as "Five steps." Then I will ask another student to measure off in steps how far apart the two stationary students are. Her answer might be "Three steps." Next we'll use a meter stick to measure the distance so we have a fixed unit. I can ask, "What will happen if so and so starts at this number three spot and takes five steps?" Most of my students are going to say that it is somewhere over to the right (in the manner in which we count left to right). But—I will have that student start at the "3" and actually walk five steps to the left (secretly, of course!) Oh my—this can't be right, they will think! That is when I have their rapt attention and can introduce negative numbers! So, now I must ask, "When we are working on the number line, what else do we need to know besides the distance?" The answer to that is "direction!" There is one math standard regarding negative numbers at my grade level, and that has been selected to be "compacted," which essentially means there isn't time to teach it, however knowing about negative numbers is critical in algebra so whenever I have an opportunity talk about negative numbers, I will do so.

Addition and Subtraction

Prior to introducing the concept of multiplication on the number line, I want to take an opportunity to look at addition first. The reasons are twofold: Addition on the number line represents a translation; and, my students need to have a firm grasp of place value. With addition, there is a conceptualization hierarchy:

1. addition is combining heaps of things, which has a length measurement analog;
2. addition is also combining rods end to end which can be automated using the number line;
3. addition can be accomplished automatically using the number line by combining rods in a standardized way: put one rod on the number line with its left end at zero, and the second rod adjoining it on the right, then you can read off the sum from the location of the right hand end of the second rod.
4. if you add a fixed number to a variable number, the answer is always some units to the right of the other number, so that addition can be thought of as giving a translation x→ x + a of the number line.

If you think about a simple problem such as Fallon had 43 pennies and her mother gave her 68 more, this can be represented in the four ways above.

1. In combining heaps, count 43 pennies and put them in one pile. Then count 68 pennies and put them in another pile. We can combine the two piles, but still need to figure out how many there are altogether. It makes sense to sort them into piles of ten. Students may want to do this with the two groups to begin with, but if not, let them see that it is much easier to work with piles of ten, rather than random groups of coins.
2. Another way I want to show this problem would be to use ten rods and cubes. On the floor, we can lay out four ten rods and three one cubes. Then we want to add the six ten rods and eight one cubes. We have to talk about why we would want to rearrange the rods and cubes in order for all the rods to be together end to end, and then the cubes all together. This kind of representation can be a key to understanding place value. Since we'll have eleven ones cubes we've got to figure out what to do with them. I expect some students will know that once you have ten, you want to put them together to form a tens rod, and at that point you can exchange one rod for the ten ones since they are easier to work with. I think it will be beneficial to take some time to show how this procedure with the ones and tens rods can be extended to three digit addition in order to emphasize the quantity aspect of the base ten decomposition of a number. Even doing four digits is possible, albeit a bit unwieldy! I have access to a large supply of manipulatives, and I can work in the hallway. I think it will be quite amazing for my students to actually see one hundred tens rods lined up in a row in order to show what a one thousand rod would look like! More importantly, this is a superb way to demonstrate the absolute efficiency of our place value system.
3. Using the number line and base ten rods, one begins at 0 and counts 43 units to the right (or four tens and 3 ones), then starting at the number 43, you count 68 (6 tens and 8 ones) units more until you end at the number 111. You want students to be able to see that the first line segment of 43 units is shorter in length than the second segment of 68 units and the second segment of 68 units is shorter than the two line segments put together, and the two line segments end to end are larger than each segment individually. The child can see she is combining and separating because a number line is a template with which to actually see and compare the length of the line segments or distance.
4. Finally, we can use the same numbers to show the problem on a number line. With 0 being the origin or beginning point on the line, we will count to 43 to show that Fallon had 43 pennies to begin. From 43, we will count on 68 more units to represent the pennies her mother gave her. Starting at 43, we will count 1, 2, 3, etc. and stop counting when we say "68." The last digit we land on will be 111. Counting by ones is not the most efficient way to add, but in the beginning I want my students to have complete understanding that each place on the line represents a unit of one. Therefore, we began with x=43, then showed that 43 + a, or 43 + 68= 111.

Different terms can be used to talk about the movement on the number line. I can call the moves on the line "jumps," or I can say "stepping out" by a certain number. I want to teach my students that there are different ways of describing the movement on the number line, however no matter what one calls them; the terms refer to the movement along the line.

I then want to take some time to solve subtraction problems using the same numbers in previous problems. I would ask, "If Fallon has 111 pennies now, and she started with 43, how many did she add? I need to make certain that my students understand that subtraction is the inverse of addition; it is an undoing of the addition problem. Students are often unfamiliar with the language of word problems and don't immediately recognize this as a subtraction problem. I want to spend enough time using the number line to explain addition and subtraction before moving on to multiplication, but I will teach a unit later specifically on regrouping with three and four digit numbers, so I know I will have an opportunity to revisit all that I have taught here.

Multiplication and Division

In the multiplication unit I currently teach we use the array model, so students can visualize what multiplication represents: combinations of equal groups. The foundation for this unit is an area model for multiplication: equal rows and equal columns make a rectangle. I know it is common to teach multiplication as "repeated addition" but studies show that it actually confuses students later when they start multiplying fractions, so I don't want to teach them this terminology. In the context of stories, children are reintroduced to multiplication because they were first introduced to the operation in third grade. I place a certain number of colored square tiles for the overhead on the glass and ask how these tiles can be arranged into rectangles.

If I place twelve tiles on the overhead, one student may come forward and make three columns with four tiles in each column. Remember, rows are horizontal and columns are vertical. We will talk about what this means: If we pretend that the tiles represent cookies, and the student wanted to share his cookies with his friends, then his picture shows that he and two friends would get four cookies each. So the number sentence representing the pictures looks like this: 3 x 4 = 12: three rows, four tiles in each row, so each child gets four cookies. Some students will forget that they are part of the equation, so that is why he is sharing with two friends, he and the two friends make three. I would invite a different student to come forward and find another way to share her cookies. She may decide to take the twelve tiles and arrange them into two rows with six cookies each. That means she will share her cookies with one friend and the two of them will have six cookies each. I would probably point out that she likes cookies very much! The number sentence representing her picture is 2 x 6 = 12. The next student may decide to place the tiles in six rows of two, 6 x 2.

Once my students have exhausted all possibilities for possible rectangles with twelve tiles, I want to do some comparing of the rectangles side by side. I want to ask, "Is the two by six rectangle the same as the six by two rectangle? Is sharing twelve cookies between two people the same as sharing twelve cookies between six people?" The answer is "no." There is a fundamental difference mathematically between these two representations. I will analyze each pair of seemingly similar rectangles with my students. I want them to recognize that even though they appear to be the same, mathematically they are not. However I will teach them that 2 x 6 = 6 x 2 because we can convert a 2x6 rectangle to a 6x2 rectangle by rotating it 90 ^o. We do end up with the same answer, but we don't arrive at that answer in the same manner. I will give my students many opportunities to explore this concept so that they understand it fully.

There are many problems we work out with different numbers of tiles so students understand that the rows and columns must always be uniform. The numerals that represent the rows and columns are called factors and the total number of tiles is the product. When skip counting with students we call those numbers multiples. A given number of copies of a given number are a multiple of that number.

Next, I will introduce multiplication by means of a measurement model using the number line. Since I will have already introduced the number line and how to use it to do addition and subtraction, I think my students will be ready to grasp the notion of using the number line for multiplication. A number on the number line represents the signed distance from the origin. Multiplication may be interpreted geometrically as dilation of the number line by a constant factor. If we have an equation: y=ax, let a equal the constant. Now replace "a" with a number, 3 for example, and let x represent the positive numbers 1-12. So, y=3x1, 3x2, 3x3, etc. A transformation occurs on the number line based on the scale factor. Again, this model offers another geometric model for multiplication as stretching of the number line. The length of each interval is stretched by the given constant factor.

This is a very different way of thinking about multiplication which is not often taught to elementary students. I am still focused on factors and products, but the process is quite different. We are not building a model, but rather using a model to move along at intervals to find a product, or moving to the left if we know the product and one of the factors. If we have a number line with the units marked in segments by ones, 4 x 3 would look like this:

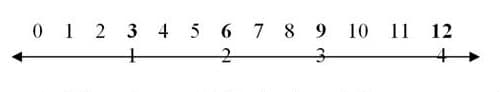
I will introduce multiplication in a similar manner used in the array lesson: If one wants to jump to 12 on the number line, what are different ways one can get there? You want to have equal groups or spaces between jumps on the number line, and you want to land exactly on 12. Students will see that they can make twelve jumps of one or six jumps of two, three jumps of four and four jumps of three, two jumps of six, and finally one jump to twelve. We will write number sentences to describe these jumps so they will see the relationship between jumps on the line and factors and products. We will continue to explore this method using different numbers such as 15, 16, 18, 20 and 24. These are the same numbers students use to explore arrays in the unit, so we can make a connection to the array model now using paper strips of a number line. Still working with the number 12, we can cut the strip representing the product into equal pieces, and stack these pieces on top of each other to make the array/area model. Following are some of the key differences between the area model and the number line model:

1. The array model clearly shows the two factors, but it does not make as clear that the product is a number.
2. In the area/array model, the product is measured in different units than the factors, but on the number line, both factors and the product have equal status.
3. In the array model, the two factors are more alike than in the number line model. In the array model, one factor is the size of a row, the other is the size of a column; but these can be interchanged by reflecting or rotating the array.
4. In the number line model, one factor is the length of the original interval, and the other is the dilation factor, represented for whole numbers by the number of intervals laid out.

Once my students complete these activities, they will work in teams to model multiples of the numbers 2-12 on the number line. For instance, if a team is working on dilation of the number line by two, they will show one jump from 0 to 2, and writ on an index card "x 1" to represent that movement, that is one jump of two. Index cards will be placed to the right of the number line. I want them to model factors from 0 to 12 using their given scale. They will use colored strips of paper to make their models of multiplication using the number line. What I envision they end up with is a sort of pyramid representing each number of jumps on the line. Using the example above, the team would draw a number line on one colored strip of paper. They would show one jump, from 0 to 2 with an arched arrow. They write the corresponding number sentence and tape that and the strip with the number line on the wall. Next, they use another piece of register tape to show two jumps, from 0 to 2, and 2 to 4. That shows two jumps of two, or "x 2." That is written on a card and together the number line and the index card are taped above the first number line. These should all be lined up over a numbered number line, so that any product can be read off readily. They will continue in this manner until they have modeled all the facts from 1x2 to 12x2. We will develop a strategy for marking off uniform intervals so this presents an opportunity for some problem solving. (For example, the children might decide to use the floor tiles as even intervals so they will know where to place the numerals on their number lines.) The largest product we will have to represent is 144, the product of 12 x 12. While that will require a very long piece of register tape, it certainly will provide a clear visual representation of multiplication on the number line! The whole activity should result in a colorful display that will make the dilation aspect very visible.

At some point during this unit, I will show my students how they can "chunk" a problem so that it is easier to solve. For example, if I give the problem 8x7, a student may not know the answer to that but he can solve 8x2=16 and he also knows that 8x5=40. He then uses those facts to figure the answer to 8x7: 16 + 40=56, the answer to 8x7. This is a nice introduction to the distributive property which looks like this:

8x7=8x (5+2)

=(8x5) + (8x2)

=40 + 16

=56

Since both models for multiplication are visual, it is possible to demonstrate this visually with square tiles and number lines. On the overhead, I will construct 8 rows of 5 tiles, and 8 rows of 2 tiles. We will find the total for each rectangle and add those two numbers. On the number line, we will have our strips with the same numbers: 8 jumps of 5, and 8 jumps of 2, and once more we will add the two together to reach a total of 56. Students later learn a strategy called the "break-apart method" for two digit multiplication, which is the essence of the distributive property, so including this piece of instruction here will provide a foundation for teaching and learning that will follow.

With both the array model and the number line model, I will show how division is the inverse of multiplication. Many of my special needs students struggle with this concept when presented with word problems so I know it will take a lot of practice and reinforcement for them to internalize this idea. Fortunately, the number line makes measurement division quite clear by its very nature. Once they know how to find a product by moving a certain number of jumps on the line, I will show how division is just the undoing of multiplication. A problem such as this: "We are having a barbecue. If we have 16 hot dog buns, and each person will eat two hot dogs, how many people will that feed?" can be solved by beginning at the number 16 on the number line, then skipping back by jumps of two to land at zero. By circling or highlighting our jumps, and then counting, students will clearly see that eight people will be able to eat two hot dogs each.