Content
I have had the pleasure of teaching second, third, and fourth grade students. There was something that I noticed about the grade levels that I have taught: students were unable to complete basic computation problems. As I spoke with teachers that taught different grade levels, they also were having the same problem with their students not being able to complete basic computation problems. Many teachers believe that this problem exists because math programs have moved away from the "skill and drill" method. Others believe that students are being exposed to material that is difficult and confusing. I find the perspectives that teachers have shared with me to be quite interesting. Over the years I have felt like I need to crack a special code to help my students be successful with computation problems. After participating in Roger Howe's seminar at the Yale National Initiative, I believe that I have finally cracked the place value code with regard to basic computation problems. The code is to establish a firm foundation with the base-ten system, which needs to be built early on in a child's education. A strong understanding of the base-ten system will allow students to understand place value and be successful with computation problems.
There are two foundation skills that will be discussed several times throughout this unit: base-ten number system (decimal system) and place value. The base-ten number system is a number system that represents numbers. The numbers usually correspond to the number of units in a given set. This number system is composed of the numbers 0, 1, 2, 3, 4, 5, 6, 7, 8, and 9. The reason it is called the base-ten number system is that it is devised of ten numbers. When the numbers bond together, they determine the place value for the given number. Place value is the placement of the number within the decimal system. For example, 9 + 3 = 12, which has a 1 in the tens place, and a 2 in the ones place. Later in this unit we will stress the importance of thinking of the number 12, for example, as a sum of its place value components 10 and 2. Please remember "decimal system" is referring to the base-ten system.
Mathematicians and educators have been studying and learning about math programs being used in the United States, and what they have found is that schools in the United States have been emphasizing the "skill and drill" method. Many people believe skill and drill is the answer to helping students to understand math computation problems, but it isn't. Skill and drill is a quick way to get the information into a student's mind, but it doesn't provide them with logical reasoning and understanding of how the answer is derived. Logical thinking is what prepares students for tougher mathematical concepts later in their educational careers. A reason that this method isn't beneficial is because a student may know a fact one day and be unable to recall the fact the next day. If you build logical reasoning, when they are having difficulty, they will be able to use reasoning skills to produce the answer to the computation problem.
Another interesting discovery that mathematicians and educators have discovered is that Singaporean students are excelling in their math computation skills. 1 The question that this has sparked in me is "Why are Singapore students so successful?" The answer, I discovered, is that Singaporean teachers aren't expected to teach a lot of content units. Instead, Singaporean teachers have identified just a few skills as essential. The teachers work on the identified skills extensively until the students have them mastered. I then began to reflect on the Common Core Standards being adapted here in the United States. 2This trend of thinking is evident with the Common Core Standards. A set of essential skills have been identified for students to learn at each grade level. I immediately thought back to when I first began teaching thirteen years ago. I had several performance indicators (standards) that I was expected to make sure my students had mastered. Later, the standards were revised and I had fewer standards that I had to make sure my students had mastered. So, as you can see, it seems the United States is moving toward adapting the same philosophy as the Singaporean model. The Singaporean philosophy is to teach less, but make sure that a great deal of instruction occurs with these few concepts and that students master the skills being taught.
I have spent a great deal of time researching the Singapore Math Program. This program is commonly referred to as "Primary Mathematics" in the United States. I chose to look at this program because as mentioned before, they are excelling in mathematics in Singapore, and I wanted to find out what skills they are using. One thing I did notice about the textbooks in the Primary Mathematics series is that three main features are discussed in the beginning of each book. Those main features are: conceptual, pictorial, and abstract (algorithm). Students should be successful at each of the above steps prior to moving on to the next step within the process.
The first step is conceptual. During this step, the students get a firm understanding of what is being asked in the context of the given situation. Students will know why math ideas are important and when to use the skills. During this step of the process, new ideas will be associated with old ideas. Linking new ideas with old ideas helps students to relate to new information better. The second step, pictorial refers to linking pictures with the mathematical concept. Students will use manipulatives or draw pictures to illustrate the concept that they were just taught. Once the students have a firm understanding of the conceptual and pictorial steps, the third step, the algorithm is taught. The algorithm is a step by step process for solving a math problem. Within the United States, we have been accustomed to working with the algorithm and not emphasizing the conceptual or pictorial step. I then began to wonder why many educators are changing things now after we have been doing it the other way for so many years. What I have learned from my research and during my time in the Yale seminar makes sense. Algorithms are very abstract. The symbols used can be as complex as the procedure used in any given computation problem. Given the fact that the algorithm is so abstract, the student focuses on the procedure needed to solve the problem instead of understanding what the symbols mean. The next thing I noticed is that with this new way of presenting information, parents begin to feel helpless with helping their children. I try to reassure them that it is a process with a purpose. The algorithm will be introduced, but not until a bit later. Unfortunately, there are still some parents who feel the need to continue with sharing their philosophy with their child. I try to remind them of Roger Howe's math rule: "Shortcuts are for the experts!" I hope that this will be the motivation that my parents need in order to withhold the algorithm with their child until the appropriate time.
Many math programs in the United State have begun to adapt concept driven math programs. What I have noticed is that with the implementation of these new concept driven programs, some of the previous skills that were taught have been lost. One of those previous skills would be an emphasis on the base-ten system described earlier. Since this is the number system used in the United States, it is important that I expose my students to this primary number system. By spending time with the base-ten system, I aim to build a firm foundation with numbers. This firm foundation will prove to be beneficial later by allowing my student to be flexible with numbers. Because my students are flexible with numbers, they will be able to complete mental math problems with a great deal of proficiency.
All of the above research has made we wonder, "What would be the most appropriate way to teach my students how to complete computation problems?" During my seminars with Roger Howe, he shared four steps that he urged be established early in an elementary mathematics program to lead to success in computation problems. Each of these steps is extremely important. The four steps I am about to share follow the three steps mentioned above: conceptual, pictorial, and abstract. I never move on to the next step if the current step isn't understood. Moving to the next step prematurely will create frustration and will hinder a students ability to be successful with completing future steps. During this unit, I teach skills simultaneously and not separately as they may appear in current and previous math programs. Concepts are being taught simultaneously because I don't want my student to view them as two separate skills. I want my students to see the relationship between the skills. The discovery of this relationship will allow my students to become great with mathematical computations.
In the next section, I will discuss Howe's four steps mentioned above. I personally found the information that was shared to be quite informative. I hope that you will see how cracking the place value code will help your students be successful with understanding place value.
Flexibility with Facts to 10 and Decomposing Tens and Ones
All students need to be flexible with adding and subtracting number facts to 10 and decomposing teen numbers into tens and ones. Students knowing facts to 10 is a first foundational step towards successful addition and subtraction. Students should be taught their facts without flash cards. Working without flash cards allows my students to become flexible with the parts of numbers that can make a specific whole number. A flexible number sense should lead students to think of the many possibilities of how numbers can used to solve problems. Repeated work with numbers will also help students become familiar with their addition facts and recognize them instantaneously. Rearranging numbers to obtain a certain sum or difference is a great way to reinforce the facts without making it a memorization process. If you give the students the number 6, they should be able to give you the following numbers as sums of 6:
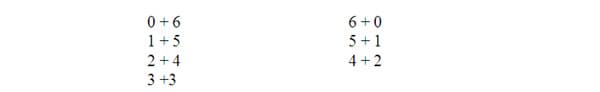
(They do not have to been in the correct order as I have presented them.) I would introduce inverse operations next, which "undo" the previous equation. So, if you have addition, what is the inverse operation? Yes, subtraction is the inverse operation of addition. I introduce subtraction with the following steps: 6 – ___ = 4 (2 goes in the blank). Working with these same numbers, one can form "fact families":

Fact families are a collection of related addition and subtraction equations or inverse operations. However, I am not separating this concept as it is often presented in math programs. Being able to decompose the numbers as explained above will help students to learn how to decompose larger numbers later. Starting with smaller numbers will help you to ensure that your students understand the conceptual part of this process before larger numbers are used.
Using Facts to 10 to Decompose Tens and Ones and Add and Subtract Facts to 20
Once your students have a firm foundation of the facts to ten, spend some time discussing the teen numbers. The teen numbers are 11, 12, 13, 14, 15, 16, 17, 18, and 19. I never considered the teen numbers as being unusual prior to my seminar with Roger Howe. However, in his seminar, he mentioned that teen numbers have funny names: eleven, twelve, thirteen, and fourteen are the most abstract. Fifteen, sixteen, seventeen, eighteen, and nineteen are weird, but a little bit easier to understand than the previous four. Unlike the base-ten number 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, teen numbers do not have a great correlation with their names. Therefore, the number words for teen numbers give an appearance of being abstract for younger children. In Singapore, they have a technique for introducing these numbers to their students, that I feel will help with understanding the teen numbers. They teach the numbers with an emphasis on the base-ten system. When teaching the teen numbers, I use number cards. Eleven would be taught as one ten and one one, twelve as one ten and two ones, thirteen as one ten and three ones, and this technique would continue until all teen numbers were taught in this manner. Next to the numbers I would use a card with ten written on it and a card with the number of ones written on it. They would be overlapped a little to emphasize that the two numbers need to bond together to make eleven.

By introducing the numbers this way I allow my students to relate numbers to the base-ten system. The introduction of numbers in this manner also gives students a concrete relationship between the number, word, and the amount the number is representing.
Once student have a firm grasp of this concept, I teach them how to add and subtract by decomposing numbers with the same strategy as I used with the teen numbers. Here is an example of what I am expecting from my students: given the problem of adding 13 + 7, I want my student to recognize that 13 can be decomposed as

so that 13 + 7 = 10 + 3 + 7= ___. Then I would like for them to realize that 3 + 7 = 10. Finally, they would say 10 + 10 = 20. The methods I have described above help students to be flexible when trying to answer computational problems.
Here is an example for subtraction: given the problem of subtracting 19 – 3 = ___, I hope that my students will realize that 19 and be decomposed to
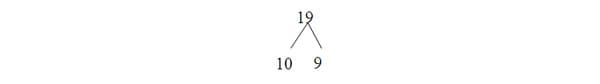
and therefore that they are solving the problem 10 + 9 – 3 = ___. Next, I want them to recognize that nine can be decomposed to 6 + 3. The equation has now become:
10 + 6 + 3 – 3 = ___. Right away my students will ideally recognize that 3 – 3 = 0 due to my work with inverse operations described in the previous step. Finally, they arrive at 10 + 6 = 16. Again decomposing numbers allows for students to be flexible with their addition and subtraction and more fluent with math computations.
Decomposing a General Two Digit Number into Tens and Ones
After students successfully carry out addition and subtraction within 20, and gain comfortability with decomposing these numbers into tens and ones, the next step is to carry out these same ideas with general two digit numbers. The numbers that I focus on during this step are the "ty" number. The "ty" numbers are 20, 30, 40, 50, 60, 70, 80, and 90. The goal is to get my students to realize that 20 is composed of two tens, 30 is composed of 3 tens, etc. Once this connect is made, I will look at numbers with tens and ones. An example would be 34. I am expecting my students to tell me it has 3 tens and 4 ones. Once again, number cards are a useful tool to illustrate this. For example, to illustrate the decomposition of the number 34, I would have a 30 written on one card and 4 written on another card. The two cards would be place over one another so that they overlap. Using number cards in this way helps students to understand that the numbers have to bond together to make 34. I practice this with a lot of intensity so that students become fluent with decomposing numbers. The more practice they have will allow the concept to become second nature for them when thinking about two digit numbers. By developing this skill early in my students' educational career, they will increase their abilities and to complete mental math calculations. It is also important to pay attention to how your students talk about numbers. If you ask your student "What numbers make up 32?" 3 and 2 is an incorrect response. Students should respond with either 30 and 2 or 3 tens and 2 ones. This is a great way to emphasize what you just taught them. Decomposing numbers into tens and ones will lend itself nicely to the next step in this process, adding and subtracting number.
Add and Subtract General Two Digit Numbers with Decomposition
By this point in the process a firm foundation of the base-ten system has been established, a great deal of time has been spent with decomposing numbers and the first two steps in the Singaporean approach described earlier. By now we are ready to begin working on general addition and subtraction, and using the algorithm, the third Singaporean steps. The algorithm is a very abstract method, but the foundations previously established in the base-ten number system will aid in students' understanding of the algorithm and what they are being asked to calculate. In the process of learning flexibility with numbers as described above, students will develop their logical thinking skills, which is extremely beneficial in adding tens and ones. As the numbers become larger in their mathematics education, students will reflect on the base-ten model that has been taught as their foundation and they will know that numbers can be decomposed.
If my students are presented with 23 + 32 = ___ for example, I am expecting them to decompose the numbers as follows:

Next, I want them to add 20 + 30 = 50 and 3 + 2 = 5 together. They should arrive at
50 + 5 = 55. Prior to this method being shown to them, they may have felt the need to use a calculator because the numbers were so large and overwhelming. I always tell my students "In math, you can move your numbers around to make it comfortable for you." After this seminar I need to say "You can decompose and move numbers around to make it easier for you." Here is an example of what I am expecting in subtraction. 45 – 32 = ___. I would expect the problem to be decomposed as follows:

Next the multiples of ten should be subtracted from one another: 40 – 30 = 10 and the ones subtracted from one another 5 – 2 = 3. Therefore, the final answer should be 10 + 3 = 13.
You might be thinking that the previous examples are somewhat special. Indeed, there are two additional very unique situations that can occur in addition and subtraction: "regrouping" and "borrowing". Essentially with regrouping you have enough ones to make a ten and still have some ones, so the extra ones are moved to the tens place as one ten. So, if you have 15 ones, it can be written and one ten and 5 ones. Here is an example of how students think about a regrouping situation. Given the problem of adding 32 + 29 = ___, students who have gained a comfortablility in decomposing numbers into their place value numbers would decompose the numbers:

Next, they should add their tens and ones: 30 + 20 = 50 and 2 + 9 = 11. As you see, we have 11 ones. This can be decomposed to 10+1. So, they will take and at the new
10 + 50 = 60. The equation now becomes: 60 + 1 = 61.
The second situation that occurs, borrowing, occurs in subtraction. Essentially, this means you don't have enough to subtract a number from another number, so you move to the next place value to get help. Here is an illustration of borrowing using the base-ten system. Given the problem 80 – 33 = ___, students should now know to decompose 33 as 30 + 3. When they are then faced with the fact that they can not subtract 3 ones from the 0 ones found in the number 80, they should decompose the number 80 as 70 + 10. Thus, they are left with the decompositions:

Then students should subtract 70 – 30 = 40 and 10 – 3 = 7, so 40 + 7 = 47.
I could also begin to develop measurement skills by using the number line. In my research I discovered the saying "We can't subtract a bigger number from a smaller one", (for example the "0 – 3" that students first encounter in the example above), is false! The reason for this being a false statement is that later on, students will learn to subtract a bigger number from a smaller number. If you are telling them this now, they will think that it is impossible to complete their future math computations later. Also, instead of referring to it as borrowing refer to it as decomposing. As you can see, this process has begun to crack the place value code early on and will help my students be successful with their mathematical computations!

Comments: