Background
The goal of the unit is to have my students be competent and confident in working with numbers of all sizes, using the tool of scientific notation. To accomplish this, I will have them work with sets of numbers drawn from various topics of interest, with an emphasis on astronomy, since that is an important topic in our syllabus, but also from other areas that should interest them. For example, an early lesson might discuss the volumes, masses, and densities of the planets and the Sun. Other topics I plan to deal with include:
- Currency Values
- Wealth and Income
- Time
- Distance
- Size
- Information and memory in computers.
- HR Diagram
One of the high points will be discussing size, temperature and luminosity of stars,
as encoded in the Hertsprung-Russell diagram.
Students should understand that base 10 notation is a concise method for writing numbers, in which the position of each digit determines it value. They should easily be able to identify the place value of numbers up to three digits, including the one, tens, and hundreds place. This also applies to either side of the decimal point, where the three digits to the right represent tenths, hundredths and thousandths. Next students need to understand how place value operates. They should recognize that an increase of each place value represents an increase by a factor of 10. The same is true for a decrease in place value with the place value decreasing by a factor of 10. This makes the next place value 10 times bigger or smaller depending on which direction the place is moved.
To help express this idea, students will practice decomposing numbers like 752 into 700 + 50 + 2 showing the value of each digit in the number. We will call the individual terms like 700 and 50 and 2, single place numbers, since each one has only one non-zero digit. It should be explicitly discussed that these numbers could be expressed using the power of 10 just as our base 10 number system describes. This can easily be done by writing each 'single place number' as a-digit-times-a-power-of-10. Students will perform that task by explaining how 752 can be expressed as 7 x 100 + 5 x 10 + 2 x 1. This notion becomes even more clear when it is expressed in exponent notation as follows: 7 x 10 2 + 5x10 1 + 5 x 10 0. As mentioned before this pattern of notation can be used on both sides of the decimal place. To continue with this idea, students will write out how 58.33 can be expressed using scientific notation. Many students may come up with the following as an answer:
5 x 10 1 + 8x10 0 + 3 x 10 - 1 + 3 x 10 - 2
If done correctly this should prepare the students for how notation also explains how the Law of exponents works, giving the reciprocal of the number when it is represented by a negative exponent. Simply put, changing the sign of the exponent turns a power into its reciprocal (i.e. 10 - 1 = 1/10, 10 - 2 = 1/10 2 or 1/100). A lesson on fractions is not included in this unit, however it can be explored if needed.
The conclusion of the previous activity will lead us to compare the sizes of the single place numbers. The idea here is to get the students to understand the significance of the single place numbers and eventually how rounding makes numbers easier to understand. Therefore, students will compare the sizes of all single place numbers identifying which numbers are greater than others. They should conclude that the largest single place number is larger than all others combined. For example, in the number 752, the 700 is larger (in this case, much larger) than the 50 + 2. Further, the 700 + 50 already represents almost all the number. The missing 2 is negligible for many purposes.
Similar reasoning applies to numbers of any size. If we take
7,524 = 7000 + 500 + 20 + 4,
then the 7000 is (again, much) larger than the 524, and the 7000 + 500 = 7500 is much much larger than the 24 represented by the last two digits. It is always like this.
This is the motivation for scientific notation. If we have a number like
752 = 7x10 2 + 5x10 1+ 2x10 0,
then the largest base ten unit involved in it is 100 = 10 2. The idea of scientific notation is to express the number relative to this unit. So we write
700 = 7x 10 2 , and 50 = 5x10 1 = 5x10 - 1 + 2= (2x10 - 1)x10 2, and 2 = 2x10 0 = (2x10 - 2)x10 2 .
Putting these together gives
752 = 7x10 2 + (5x10 - 1)x10 2+ (2x10 - 2)x10 2 = (7 + 5x10 - 1 + 2x10 - 2)x10 2
= (7 +.5 +.02)x10 2 = 7.52x10 2 .
Thus, the whole number is expressed as a multiple of its largest base ten unit. This is the basic idea of scientific notation.
Further inspection of this idea will lead my students to understand the role of accuracy in scientific notation. For example, they will compare the first two single place numbers to each other and identify that the first two are ten times larger than all others combined. Taking it one step further the students will be asked to take the first three single places and come to find that they are at least 100 times larger than all the others. This will lead to their understanding of how significant figures are determined by observing how stating a number to its first three places gives you very good approximation of the original number. A student then may ask for an example of such a scenario. Comparisons will be made to objects give you accurate estimations by rounding to the first three place, like the radius of the Earth, which is approximately 4000 miles (More accurately, 3960 miles, or about 1% less). Here they will see that the error made in this estimation is unimportant for the most part. They will find that two or often, even one digit gives you a good approximation. This will be made clear in each step by rounding the numbers to the first one, two, and three places.
It is essential to reiterate the realization that scientific notation makes computation of large and small numbers quite simple. Students might believe that numbers of these magnitudes are too difficult to compute because of their size. However, if the students identify what scientific notation does to a number, they can begin to accept the reality of how simple calculating these numbers can be. To capture these ideas, students will be asked to use zeros to represent single place numbers. This will be followed with instructions to attach exponents to the zeros in the single's place and write out the proper notation. They should respond with answers that look like the following:
10 3 = 1000, 10 5 = 100,000, 10 7 = 10,000,000.
Hopefully, by performing this task students will begin to see how the process of factoring out the largest power of ten allows us to obtain scientific notation. It also saves us the time of writing all of those zeros. This will help to highlight the value of using scientific notation.
For students to completely understand scientific notation they must become more familiar with how to write out the notation. To help with that, students will be given a set of numbers and asked to convert those numbers into scientific notation. For instance, they will be given the number of seconds in a year to be 31,560,000.0 and then asked to convert to the most appropriate form of scientific notation. Another problem might give them the mass of the sun to be 1,989,000,000,000,000,000,000,000,000,000,000 grams in which they would have to convert the number to the most appropriate form of scientific notation. They could also be asked to give the closest approximation to each number as they can, using rounding techniques. This should get them to realize how rounding a number is connected to the notation of the number.
In addition, they will again be asked to round their answers to a specified number of significant figures, i.e. 1 st digit, two leftmost digits, etc. The reinforcement of this idea is critical for obtaining the objectives and will remain a common theme throughout much of the unit. They will follow that by comparing the rounded numbers to the actual value, and expressing each difference as a percent error. This will help them to see that the main information is found in the leading digits. To add rigor to the lesson, I will ask my students to express the numbers in different units. For example, they could convert minutes to years, or kilograms to milligrams. This purpose of this activity is to get my students to understand what numbers are significant and how their magnitudes are affected when the units are changed. This will also lead into a discussion on accuracy, which will be discussed more thoroughly later in the unit. More problems to practice their writing of scientific notation can be found in the appendix.
Another example that could be used to employ the order of magnitudes is money and how its applied to everyday life. The examples will take a specific value, like the value of money in Zimbabwe (1 Zimbabwe dollar = $10 - 1 7 USdollars), and compare it the value of money in the United States. When they compare the numbers they should keep in my mind the theory of a base ten number system and recognize how significant the difference is. They will be able to do so by subtracting values from one another writing out the value in scientific notation.
In addition, they could be asked how much a pile of million dollar bills in Zimbabwe currency weighs, if each Zimbabwe bill were the same size as an American dollar, and the total pile was equal in value to one American dollar. (The weight of a dollar bill can obtained via web browsers on the Internet) Then to ensure their understanding they will be asked discuss the differences in the two problems. By computing these numbers students recognize the way notations of a number can make concepts more clear. Several more problems like the ones above will be used to reinforce the idea that scientific notation can represent magnitudes of very big and very small numbers. These problems can be found in the appendix. It should also be noted that many of the problems given would require access to additional information via the Internet or any other database of information.
Then students could then be asked what the ratios imply and if any connection could be made about earth and moon behaviors because of the ratio between the mass of the earth and moon. Understanding ratios will further lead the students on a path of connecting accuracy to scientific notation. Additionally, comparing very large numbers and finding normal sized numbers to replace these very large numbers can get students to see that these large numbers can be handled quite easily and can produce information they can comprehend. Additional problems on comparing magnitudes and comparing their ratio can be found in the appendix. What follows will be examples of activities that are meant to emphasize the relationship that accuracy shares with scientific notation.
When evaluating different sets of data, scientists depend on the accuracy of results. Accurate data provides scientist with the reliability they need when declaring theories and laws of science. This is found to be true in many other activities as well, including the government and pharmaceutical industries, where the accuracy of numbers can have dramatic effect on profitability. The complexities of science sometimes determine the accuracy of results. Often, the more precise the science, the more accurate the results need to be. The inaccuracy of results in science and the industries mentioned above could be costly and fatal depending on the circumstance. Frequently these results are given as estimations. Estimations help when calculating very big or very small numbers by eliminating many insignificant numbers and focusing on the numbers that matter. These numbers tend to have the largest magnitude and are emphasized because their inaccuracy could cause the most change in the result. My students need to understand that basic principle to progress through the unit. Therefore, they will analyze the difference in ratios of many sets of problems and speculate on what they can infer from the differences It is important to note that estimations can often be misleading even from the most reliable of sources. My students will be given then following example to highlight this point. NASA's original claim was that the probability of a space shuttle crash was about 1 in 100,000. My students will be asked to examine this further to check its validity. After taking a closer look into NASA's claim, they will see it suggest otherwise. If the claim is true and we assume that a space shuttle takes off everyday, then we can calculate that NASA should expect to have a crash once every 300 years. This can easily be calculated by the following equation:
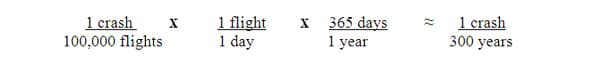
Obviously, NASA has not been fortunate enough to experience that type of probability for crashing, proving how misleading estimates can sometimes be.
Accurately expressing numbers in scientific notation, involves two main ideas. First, significant figures must be established and consistent throughout the problem. Second, relative error of estimations helps make clear the importance of the leftmost digits by comparing the ratio of the estimation to its original value. Both of the ideas allow a person to obtain a better handle on how accuracy is expressed and emphasized in scientific notation. Significant figures refers to the number of digits we are sure are correct when giving the result of a measurement. The number of digits that are usually included for significant figures rarely goes past 4 digits. Claiming any level of accuracy past 4 digits can be deceptive because it insinuates that we know more about the number than we actually do. We are limited by our technology; This leads us to only rely on numbers we can be absolutely certain about. The leftmost higher magnitude digits found in the result represent these numbers. If the significant figures are not identified at the start of the problem, my students could become confused. Students will reflect on that by revisiting the mass of the Sun. As an introductory question, I will ask the class to compute problems using the mass of the Sun. Half the class will use scientific notation and the other half will use normal base ten notation. Following the exercise my students should recognize that it was significantly easier to complete the problem using scientific notation. Accordingly, they should see that this makes identification of appropriate significant figures critically important when computing scientific notation problems.
Students will begin to understand this even more by participating in an activity that concentrates on the accuracy of the leftmost digits. They will be asked to create 10 numbers at random. The criteria for the numbers selected include: three of the digits should be over 3 digits; and 3 more of the numbers should be just 3 digits. Next, they will compute what percentage of a whole number the first digit, the first 2 digits, and the first 3 digits of a number accounts for. Furthermore, problems of this type will be reinforced through many more problems given in the appendix, leading my students to comprehend the significance of the leftmost digits. Some of the problems involve the collection of data from the Internet, making this an appropriate exercise for this developing multiple skills. They will take the problems and round each piece of data to one and two places and compute the ratios of the following: I) the numbers they find on the internet to answer basic data questions II) the same number rounded to the first digits III) the same number rounded to first two digits. Following that they could round the answers they get in I) to the first and second digit and then compare the numbers they get to II) and III). The repeated use of rounding and computing ratios will assist my students retention of the concepts and illuminate the overarching objective of the unit. They will find that they always get the same answer, or close to it (although having only one digit accuracy sometimes might lead to significant discrepancy). This will help to convince the students that they don't need very many digits before they have a pretty good handle on the number. This should be one the most valuable lessons they can learn from the unit and could prove to be quite useful throughout their life.
It is extremely important that scientists and mathematicians have a method to check that their estimations are accurate. Accordingly, an expression was devised to identify the accuracy of estimations. The following expression is referred to as Absolute Relative Difference. It also can be referred to as Relative Error or Relative Change. The expression demonstrates how accuracy can be calculated as well as the importance of the leftmost digits. It is properly utilized when we have some number/quantity represented by Q. It then follow that we approximate the number Q by Q'. Students will be given an example of that case represented by the length of the calendar year. They will read how the original calendar year was represented by 365 days, however, over time, it became clear that 365 was not an accurate account of the amount of days in a year. Thus, a new Julian calendar was submitted giving a more accurate account of the length of the year at 365.25 days. Once again, this was found to be inaccurate. This lead to the development of a new Gregorian calendar year which identifies the length of the year as 365.25 – 1/100 + 1/400. Believe it or not that number was still found to be inaccurate and today we use the very precise number of 365.242199 days in the solar calendar year. In this case we see that understanding the value of the leftmost numbers gives us insight to inaccuracies of the past. The students will then be instructed to use the equation below and take the actual length of the year and have that subtracted by the previous estimates of the length of the year. That number can then be divided by the actual length f the year, giving us the absolute relative difference. This will indicate how accurate the original estimates of the calendar year were. That situation can be represented with subsequent equations:

As expressed earlier in the unit, students learn best when the information being taught to them relates to some aspect of their life. Accordingly, included in this unit will be examples that are applicable in a variety of ways to each of the students I teach. The researched information of each example below should assist the teacher in understanding the relationship that is shared between the examples and the student. Detailed exploration of each application of scientific notation is necessary to obtain a robust understanding. As a result, the background information that follows should also be shared with the students.
A few examples that would be of particular interest to the students would be the fact that the richest man in the world, Warren Buffet, is worth more than most countries with a net worth of nearly 62 x 10 9, or 62,000,000,000 dollars. Also, the students might find it interesting that the cost of all real estate in Manhattan is at 169 x 10 9, or 169,000,000,000 dollars. (This figure is for the land only, not the buildings.) Wrapping your mind that much money can be difficult but clearly it can be seen how scientific notation could make it much easier. We could ask, for example, how many Warren Buffets it would take to buy all the land in Manhattan. After we discuss the relevance of the amount of money people possess, they will use that information to compute information relating the Sun's mass to the Warren Buffet's Wealth.
The next applications talks about the great sizes of objects in space. Much of the information that is included in this section will reinforce ideas gone over in the previous paragraph regarding time as an example for using scientific notation. However, one distinction during this section of the unit will be the focus that is given to the "Powers of 10" video that will be shown and its relevance to accuracy. In the video, the narrator discussed the way our planet along with the universe can be broken down into powers of 10. The video is extremely effective at giving the audience accurate visualizations to help comprehend how our universe is broken up into powers of 10. However, how these sizes can be accurately calculated is a mystery to the students, since there isn't a way for people to actually experience these values first hand. At this point students will begin to recognize the importance of scientists' estimation as well as how accurate they often are. In turn, this will help the students to see how accuracy is connected to scientific notation.
This concept will be carried over to the lessons when students attempt to grasp the immense sizes and distances that exist in space. There are many examples that can be used to express those concepts, including planet and star size in conjunction with distance from planet to planet and galaxy to galaxy. For size, the examples are similar in that we will compare the sizes of planets and stars to one another, all using scientific notation to express the values. Included in these examples will be another revisit to the mass of the Sun. The Sun has the greatest mass our solar system, therefore comparing other objects in the solar system to our Sun reiterates the importance and usefulness of the notation and rounding of numbers. When comparing the different values, students will take the opportunity to practice their estimation skills making the values as accurate as possible. Once this section of the unit is complete, the students will have had an adequate amount of real-life examples to apply scientific notation and master the foundations that produce the intricate yet straightforward method of manipulating numbers.
Distance
The idea of a light year is a critical concept for the students to comprehend because the many uses it has in Astronomy. However, the idea of it sometimes perplexes students because they can no wrap their minds around the actual size of the number. To be specific, the light year is used to describe distances in space. It can sometimes be misrepresented by the light speed, which is a derivative of a light year. The fact that most of space is a empty vacuum with celestial bodies sporadically occupying parts of it makes its necessary for scientific notation to exist. It helps to explain the distances of space in between these bodies since the space is so vast.
Because of its vastness the empty space in between can only practically be represented by light years. As a result, light year is represented as 10 1 6 meters, 10 trillion kilometers, or 6 trillion miles. Again, the conversion of these units can be good practice for understanding how valuable estimation can be. The introduction of the light year provides an excellent opportunity to compare the orders of magnitudes, which can be seen in the different ways a light ear represented above. Also, this will help to emphasize how size can be represented in various ways using scientific notation. This would also be a good time to point out how using only one digit provides a very good approximation of the distance one light year is. In accordance, my students will be given the fact that light speed travels at 299, 792, 458 meters per second. Then they will be given the distance from the Sun to the Earth and asked to calculate the time its takes the light to reach earth based on this information. They will come to find that it only takes 8 minutes for light leaving the Sun to reach Earth, even though it has to cover a great distance. This intends to emphasize the great distances and great speed of objects in space and how they can be managed fairly easily by using the correct notation.
Further questions that can be used to address those concepts might go as follows: How big is the solar system in light years? Or express distance of closest star Proxima Centauri in scientific notation. In addition, another tangible situation that can be used to emphasize the light year concepts considers the distance the amount of cars driven in the US travels in a year and comparing that to distance in space. The question could ask: What is the distance 150 million cars in the US and they travel in one year, if the average car travels 12, 000 miles per year? When students are done completing this problem they should share it with the class for discussion purposes. The answer should resemble something like the following: 150 million = 1.5 x 10 8, and 12,000 = 1.2x 10 4, so the product is 1.8x10 1 2 miles, which is about 1/3 of a light year! To follow up this question they could be asked how long would it take us to drive to the star Proxima Centauri at that rate? The students can then compare that answer to the different distances that specific planets are from Earth. That type of problem can be adjusted in various ways to meet the needs of students. However, yet again it is important to underscore the use of scientific notation to make these events easier for people to process. These questions are pertinent to assessing whether students are obtaining enough understanding to apply the concepts in other context. During these exercises students will experience the practice of identifying appropriate size and accuracy leading to an absolute understanding of scientific notation. Additional problems to supplement these ideas can be found in the appendix.
Luminosity, Temperature, Size
The example I will use to illustrate the application of scientific notation to temperature will involve the Hertzsprung-Russell diagram (HR Diagram). The HR Diagram compares luminosity (absolute magnitude), temperature, color and size of a star. It brilliantly demonstrates the relationship all of those characteristics share with each other. The values expressed on the diagram are very large numbers and thus using scientific notation is necessary to understand the comparisons. In fact, the luminosity scale on the HR diagram is not linear, but exponential. A change of magnitude by 1 signifies a tenfold change in brightness. I will take care to explain this carefully, and help students to read the HR diagram correctly. Once students understand what the chart is trying to express along with the way it tries to expresses it, they can then attempt to answer a problem like the following:
The Sun is 6,000 oK, how much hotter is the sun than our solar system's next closest star, Proxima Centauri? The students will also be asked to express all values in scientific notation and then interpret the meaning of the result. They can also be asked to compare ratios of the different luminosities of stars since the luminosity is represented in base logarithmic fashion using base 10 exponents to express their value (10 - 3, 10 - 2, 10 - 1, 10 1, 10 2, 10 3). The complexities of the HR diagram can be difficult to understand, however after much practice and experience with scientific notation the students should be prepared to handle the intricacies of the diagram. Their experience will help them to identify the explosion in numbers that takes place as they move around the HR diagram.
When comparing the magnitudes to one another the students can identify the differences along with how those differences correlate with other qualities expressed on the chart. Recognizing the correlation will provide students with an understanding of how movement up or down one order of magnitude (place value) can dramatically affect the qualities of stars.
Computer Science
Bits can be defined as any form of information that is converted into binary digits each having a value of 1 or 0. This may seem too simple at first, however bits can be organized in an infinite amount of various strings of bits that relay information to our computer. When the numbers start to become too big or small for practical use, they are given prefixes like kilo, mega, and giga to clarify the amount of memory being utilized.
Here, students will gain more practice with the notation and relate it to another relevant aspect of their life. This provides yet another chance for students to identify how the notation makes abstract ideas in their lives more clear. By this time, they should start to realize that the use scientific notation offers clarity on many ideas that once may have seemed too complex. Through a more thorough examination of computer science the students will identify that eight million bits is equal to one megabyte, which is the equivalent of one short novel on stored on a computer (8,000,000 bits= 1 megabyte= 1 short novel). To simplify the information even further, students will be asked to convert that those numbers and many more to scientific notation, i.e. 8 million bits can be also looked at as 8 x 10 ^ 6 bits. When finished with this application of scientific notation students should understand that 8 million bits= 1 megabyte= 8 x 10 6 bits.
Using order or magnitude to discuss computer science presents students with ideas that are tangible and relevant since computers are a major part of their lives. Identifying the connection to scientific notation allows students differentiate between memory size and the abilities that more memory size offers computers. This directly relates to order of magnitude, in that students will be able to clearly recognize that the higher the order or magnitude the more capabilities computers have. Comparing these orders of magnitude to computer memory and then to devices they use every day makes this concept evident to the students.

Comments: