Lesson Plans
Lesson-1: Introduction to the unit "There is math in your heart." Time: 50 minutes. (Suggested for Algebra-1 and Algebra-2)
Facts of the cardiovascular system from the quantitative point of view (10 minutes)
In this portion of the lesson, teacher presents facts of the cardiovascular system, which are directly related to conversion of units and scientific notation, such as diameter of vessels, flow of circulation, and pressure. Other important facts to mention are that the heart works as a pump to supply oxygen to the entire body and that the vessels divide creating more section areas, for which the pressure getting far away from the heart is each time lesser.
Class discussion about the numerical and functional facts presented (15 minutes)
Allocating a few minutes for the "why's" and "how's," and approaching the answers using students' prior knowledge, will enable the class to participate.
Learning about conversion factors and scientific notation (15 minutes)
To understand the size of the vessels, it is necessary to help students to compare the diameter of the vessels with the diameter of their wrist. After presenting examples on conversion of units and scientific notation, students solve exercises on the white board. Other options include individual small white boards or plane paper.
Closure and assigning homework (10 minutes)
A handout with exercises about scientific notation and conversion of units will be handled to the class. Examples for the homework are presented.
Lesson-2: Using formulas, Formula of area and formula of flow, what is flow? (Suggested for Algebra-1 and Algebra-2)
Presenting facts about flow, proportions and working with formulas (25 min)
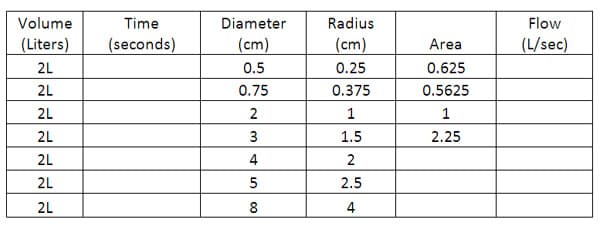
To understand flow an empty bottle of soda of preferable 2 liter will be used. Students will fill up the bottles with water, and the will measure the time that it takes to empty it, through tubes of different diameters. The data will be recorded in a table and later used to analyze the results.
Keeping the volume constant (2 liter), the time to empty the bottle depends only on the sectional area of the tube; and the sectional area of the tube depends on the square of the radius. Radius is half of the diameter of the tube.
Comparison of recorded data (15 minutes)
Flow is calculated as volume over the sectional area; therefore, in each case, the only variable is the diameter of the tubes (or the radius of the tube), because the volume is the same. The expression obtained will look like: Q = V/t, where Q is flow, V is volume and t is the time that the bottle takes to empty.
Students will fill in the blank spaces on the attached table and will find out the relationship between flow and area.
Presentation of conclusions and class discussion (10 minutes)
Students will present their results per groups. Conclusions obtained will be written on the white board or on a large sticky paper to hang it on the wall.
Lesson-3: What is Pressure? (Suggested for Algebra-1 and Algebra-2)
Lecture about pressure (10 minutes)
Using the third picture from section 4 "The Math of the Heart," explanation about understanding atmospheric pressure will be presented. The next part is the explanation of the transformation from the general formula P=F*g/A, where P is pressure, F is the force applied on area A; to the use of density and height of a fluid with the formula P = ρhg.
Practicing Exercises about pressure (15 minutes)
The last part of the lesson is to describe what blood pressure is as well as difference of pressure. At this point, some conversion of units will be presented.
Sharing solutions and explaining before the class (10)
Students present their solutions before the class
Closure and assigning homework; checking for understanding (10 minutes)
Checking for understanding will include questions about difference of pressure and conversion of units.
Lesson-4: Using series (Suggested for Algebra-2)
Lecture about sum of all the terms of a series (15minutes)
The summation of all the terms of a sequence uses the example illustrated in section 4 "The Math of the Heart," and it is based on the wrong assumption that the cross sectional area of the new vessels is exactly half of the previous one. This assumption will conclude that the sum of all cross sectional areas is equal to the initial area. Off course this assumption is not right. Using the example illustrated on figure-2 of section-4, it is demonstrated that the sum of all sectional areas of all the vessels is greater than the cross sectional area of the initial vessel.
Exercises about sum of terms of a series (15 minutes)
Students' presentations (20 minutes)

Comments: