From Arithmetic to Algebra: Variables, Word Problems, Fractions and the Rules

Unit Content

Measurements, and Units

Science is based on the collection and analysis of data, which is often quantitative in nature, represented by a number with an assigned unit. The scientifically accepted unit system (the SI system) recognizes seven base units (i.e., meter, kilogram, second, ampere, kelvin, mole, candela). The system was established in 1960, based on the meter-kilogram-second system of units, with the intention to maintain congruency among the international community. ^IV Prefixes are added to each base unit to denote multiples of the original unit by a power of ten. For example, a millimeter describes a thousandth of a meter and a kilometer indicates 1000 meters. Measurements and units are the first window into the intricate relationship between mathematics and science; they provide the context for analysis and allow repeatability in experimentation. In fact, measurements give rise to numbers through the description of a given quantity as a multiple of the chosen base unit (i.e., kilogram, meter, second).

It is essential to understand the proportional relationships among a variety of measurements to compare quantities. We will examine several problems that ask students to convert between SI and non-SI using appropriate conversion factors.

Unit Conversion with proportional relationships

1. Coach Blais brought 32 L of water to the football game, and she divided the water equally between 8

How many milliliters of water did Coach Blais put in each cooler?

Let x equal the volume of water per water cooler.

Here is the calculation of the total number of milliliters of water provided by Coach Blais.

1 liter = 1000 milliliters

1 L / 1000 milliliters = 32 L / 32000 milliliters

32 (1 L) / 32 (1000 milliliters) = 32 L / 32000 milliliters

Since there are 8 water coolers,

32000 ml / 8 water coolers = x ml/cooler

x = 4000 ml per water cooler

2. A spacecraft travels 7000 meters per second.

What is the spacecraft’s speed in miles per hour?

1 inch = 2.54 cm = 0.0254 m   60 seconds = 1 minute

12 inches = 1 foot  60 minutes = 1 hour

1 foot = 12 × .0254 m = 0.3048 meters, hence 1 meter = (1/.3048) feet ≈ 3.28 feet.

1 mile = 5280 feet

Solution I

This problem asks students to convert between rates of speed. Since the relationship between m/s and mph is a proportional one, a natural approach to this problem would be to find the unit rate: how many mph is 1 m/s?

For this solution we multiply 7000 m by 3.28 feet since we know from the list of conversion factors above that every meter approximates to 3.28 feet.

7000 m/ 1 s = x mile/ 1 hr

Step I.  (7000 m/ 1s)(3.28 ft/ 1 m) = 22,960 ft/s ≈ 23000 ft / s.

It should be noted that measurements are limited in their relative degree of accuracy, so we must acknowledge this constraint by rounding products of quantities to the appropriate number of significant figures. In our problem, the 3-digit approximation of 1 meter = 3.28 feet restricts all subsequent calculations to three significant figures thus 22,960 ft/s should be rounded to 23,000 ft/s. Rounding errors can have a compounding effect on calculations and can cause solutions to deviate. We must recognize the limitation of our solutions and use significant figures as a convention in reporting our solutions.

Once we have calculated meters to feet, the next step would be to convert feet to miles. We divide 23,000 feet by 5280 feet since there are 5280 feet for every mile.

Step II.  (23000 ft/ 1s)(1 mile / 5280 ft)  ≈ 4.3560 miles / s ≈ 4.36 miles/s

Next we convert seconds to hours, by multiplying 60 seconds by 60 minutes. We know that for every minute there are 60 seconds and for every hour there are 60 minutes thus the product of these two ratios will determine the number of seconds in a hour.  

Step III.  (1 min / 60 sec)(1 hr/ 60 min) = 1 hr / 3600 s

Finally we combine our terms from the distance (meter to miles) and time (seconds to minutes) conversions to determine the speed of the spacecraft in miles per hours.

Step VI.   4.36 mi / 1 s = x mi / 3600 s

3600(4.36 mi) / 3600 (1 s) = 15,696 mi / 1 hr ≈ 15,700 mi / 1 hr

Solution II

Alternatively, this problem could more accurately be solved using the official definition of an inch which is equivalent to 2.54 cm. Again, three significant digits are retained on all subsequent calculations for this solution since 1 inch = 2.54 cm. This ratio could then derive the ratio of meters to miles, as is discussed below.

If the official definition of an inch is 2.54 cm then we can convert this ratio’s equivalency to feet. Since there are twelve inches in a foot, multiplying the ratio of 1 inch to 2.54 cm by 12 would convert inches to feet.

Step I.  1 inch / 2.54 cm = 12 inches / 30.48 cm = 1 ft / 30.48 cm

The next step would convert feet to miles. Since we know there are 5280 feet in a mile we multiply the product from the previous step by 5280 thus for every mile there are 160,934.4 cm.

Step II.  1 ft (5280) / 30.48 (5280) cm = 5280 ft / 160,934.4 cm = 1 mi / 160,934.4 cm

The next step requires the transformation of our ratio from the previous step. Since our recorded speed of the spacecraft is meters per second, we must convert centimeters to meters. There are 100 centimeters for every meter thus we divide 160,934.4 cm by 100 resulting in 1609.344 meters for every mile.

Step III.  (160,934.4 cm )(1 m /100 cm) = 1609.344 m

1 mi / 1609.344 m

Lastly we can take determine how many miles are in 7000 meters by using the ratio that was previously determined.  

Step IV.  (7000 m)(1 mi / 1609.344 m) ≈ 4.35 miles

We utilize the same strategy from the previous solution to convert seconds to hours by multiplying 60 seconds by 60 minutes (see alternative solution).

Step V.  (1 min / 60 sec)(1 hr/ 60 min) = 1 hr / 3600 s

Finally we combine our terms from the distance (meter to miles) and time (seconds to minutes) conversions to determine the speed of the spacecraft in miles per hours.

Step VI.  4.36 mi / 1 s = x mi / 3600 s

3600(4.36 mi) / 3600 (1 s) = 15,700 mi / 1 hr

Solution III

A third approach to this problem looks to convert miles to kilometers using the conversion factors previously established. There are 5280 feet in one mile and 0.3028 feet in a meter, resulting in 160,934.4 meters or approximately 1.61 km.

Step I.  1 mile = 5280 feet = (5280)×(0.3048 m) = 1609.3440 m =

1.6093440 km  ≈ 1.61 km

The speed of the spacecraft is traveling at 7,000 m/s or 7 km/s, by multiplying 7km by 3600 seconds we can determine approximately how many km/hr the spacecraft travels. Only 3 significant digits are maintained in our approximation of miles per kilometer

Step II.  7,000 m/s = 7 km/s = (7 km/s)×(3600 s/hr) = 25,200 km/hr

≈ (25,200 km/hr)

Finally we convert km/hr to miles/hr by using the ratio previously determined in step I, again the solution is rounded 3 significant figures.

Step III.  (25,200 km/hr)×(1 mi/1.61 km) = (25,200/1.61) m/hr

≈  15,652.1739 m/hr

≈ 15,700 m/hr

This problem highlights the importance of significant figures with regards to overall accuracy of a solution. We will not touch upon this concept as it is beyond the scope of this unit but should be taken into consideration for future modifications. The systematic process of writing each proportion will allow the students to account for each ratio and solve problems that require multiple conversions. The alternative solutions will offer skills to be practiced and enable rich discussions of ratios to facilitate a deeper understanding of the derivation of measurements that quantify speed, velocity, and acceleration introduced later in the kinematics unit.

Position in the context of vector and scalar quantities

An object’s position is its location within space, defined by a coordinate system as a frame of reference (Figure 1). An object’s starting position is traditionally placed at the origin of the coordinate system, unless otherwise stated.

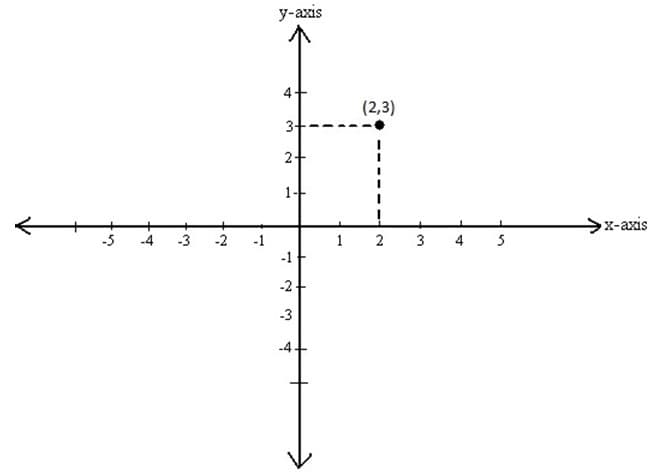
Figure 1. This illustration depicts a common coordinate system used to display the position of an object moving in a plane. We assume that the reader is familiar with the conventions of the Cartesian coordinate system, and will not review them here. However, I will make sure that my students understand these issues.

The displacement of an object is the overall change in spatial location (i.e., final position – initial position), denoted by ∆s, which includes change in direction. ^II By contrast the distance traveled by an object is the length of the total path an object travels along, regardless of direction. Both displacement and distance are measured with the SI unit meters.

Students have trouble understanding displacement, because it is a vector quantity. In general, vectors are harder to understand since both the x and y components are needed to determine direction of an object’s motion. Students will participate in inquiry investigations that differentiate scalar and vector quantities prior to the introduction of distance and displacement in the classroom (see Activities). Distance and displacement represent two fundamentally different types of quantities, scalar and vector. Essentially, an object’s physical position can be described by two classification schemas ^III. A scalar quantity is described by a numerical value that represents a fixed measurement (for example, distance and speed are scalar quantities). To describe a vector quantity, such as displacement or velocity, you need to specify a direction as well as a magnitude. Vectors in the plane, which are the main concern in this unit, can also be described by their Cartesian coordinates (x, y). These numbers, describe in this paired number notation, implicitly specify a direction. The first coordinate indicates a displacement in the horizontal direction, and the second coordinate indicates a displacement in the vertical direction. The magnitudes of these two displacements in different directions determines the direction of the vector (x, y), by a somewhat complicated formula involving trigonometry. These will be essential concepts to master prior to the introduction of distance and displacement problem sets. It should be noted that students will be asked to interpret text and diagrams to reinforce mathematic translations. My students will be interpreting and constructing graphs based on data measurements throughout the year and it will be essential for them to refine these skills to develop their conceptual understanding of rates of motion. Let’s look at some examples to illustrate the difference between an object’s total distance traveled compared to the object’s displacement.

1. A car completes five laps along an oval track 5,000 meters long. Find the car’s displacement and its distance traveled in meters.

Since the car returns to the same position as the starting position after every lap, the number of laps the car completes is irrelevant when considering its displacement. Thus there is no difference between the car’s final position and its initial position equating to a displacement of zero. The total distance the car traveled is 25000 m. This is calculated by multiplying 5000 m by 5 since the track is 5000 m in length and the car completed five laps.

Displacement

s _final – s _initial = ∆s

0 m _final – 0 m _initial = ∆s = 0 m

Total Distance Traveled

5000 m = length of track

5 = number of laps

(5000m) + (5000m) + (5000m) + (5000m) + (5000m) = 25000 m

(5000m/lap)×(5 laps) = 25000 m

2. What is the displacement and total distance traveled in the figure below? Describe the motion of a person walking from point A to point C on the position-time graph. (Note: The vertical axis of the graph indicates the distance an object travels and the horizontal axis represents time)

Figure 2. This position-time graph illustrates the motion of an object from position A to C. For this example the points A, B, and C are restricted to space in one direction.

The walker starts at 0 m at time t = 0 seconds, the walker travels 30 m in a positive direction over 25 seconds. The walker then travels 23 m in a negative direction from t = 25 s to t = 65, spanning 40 seconds. The total distance traveled is 53 m, whereas the walker’s displacement is 7 m in the positive direction. Another way to phrase the walker’s displacement is a net gain of 7 m forwards. Signed numbers have a vector component indicating over net direction along a line (e.g., left – right, up – down, or forwards – backwards). Students often find it difficult to translate graphs into words, which is essential for mastery (see Activities). Thus, decomposing the motion depicted by the graph into its components will be essential to develop translation skills. Over the course of the unit, several problems of this type will be presented, gradually increasing in complexity, with additional path segments and directions.

Displacement

 s _final – s _initial = ∆s

7 m _final – 0 m _initial = ∆s = +7 m

Total Distance Traveled

(AB) ̅= 30 m

(BC) ̅= 23 m

(AB) ̅ + (BC) ̅ = (AC) ̅

30m + 23m = d

53 m = d

Rates of Motion

Proportional relationships are essential to understanding rates of motion in physics; they compare two equal ratios. This can be written algebraically with the following equation.

x₂ / x₁ = y₂ / y₁

This equation expresses the key aspect of proportionality: a relationship between two variables is called proportional if, when one quantity changes by some factor, the other quantity changes by the same factor. For example pencils are sold in a set of 10 for 2 dollars (Table 1). If 50 pencils were bought, a proportional relationship could be setup to determine the overall cost. 50/10 = 5, that is, 50 pencils is five times as much as 10 pencils. This is the x₂/x₁ in the equation above. If I buy 5 times as many pencils, I must pay 5 times as much. This is the y₂/y₁ in the equation above. Thus, y₂/y₁ = 5 also. Since we are given that y₁, the cost of 10 pencils, is $2, the cost of 10 pencils is 5×$2 = $10.

Proportional relationships can be, and usually are, expressed in terms of a constant of proportionality, also known as a rate of proportionality, or a rate of conversion. This rate appears if we multiply the equation above that defines a proportional relationship by y₁/x₂. This turns the proportionality relationship into the relation

y₁ / x₁ = y₂ / x₂.

This equation says that the ratio of the amount of y to the corresponding amount of x is the same for corresponding the first pair values as for the second. If we fix one of the pairs of values, and let the other ones vary arbitrarily, we can conclude that this ratio is always the same, for any pair of corresponding values. This common ratio is called the constant (or rate) of proportionality. It is important to note that, although we call it a “constant”, which suggests a number, the constant of proportionality is typically not a number, but has units attached to it. For example, in our example of pencils and dollars, as the table below shows, the constant of proportionality, is 5 pencils/dollar.

Table 1. Describes the cost of pencils at a flat rate of 1 dollar for every 5 pencils.

The calculations below illustrate the derivation of the proportionality constant with regards to the cost per pencil as has previously been described.

x₂ / x₁ = y₂ / y₁

2 dollars / 1 dollar = 10 pencils / 5 pencils

The proportionality constant is found by multiplying both sides of the first equation by y₁ / x₂.

y₁ / x₁ = y₂ / x₂

5 pencils / 1 dollar = 10 pencils / 2 dollars

r = 5 pencils/dollar.

To determine the cost of 50 pencils we can setup two equal ratios with the quotient equating to the proportionality constant since we have previously determined a proportional relationship between number of pencils and total costs.

y₁ / x₁ = y₂ / x₂ = 5

10 pencils / 2 dollars = 50 pencils / y₁  = 5 pencils/1 dollar

where y₁ equals the cost of 50 pencils.

50  =  5

y₁  =  1

y₁  =  10 dollars

Many students understand rate with respect to the slope of the line between two points in a coordinate system. This fundamental concept of mathematics will be reviewed using several real-world applications. Students will describe and provide examples of rates prior to its derivation and introduction through the lens of motion.

In physics this is most often demonstrated in kinematic problems with respect to rate of change in velocity and acceleration of an object. An object that travels from one position to another over a set period of time experiences a physical phenomenon known as motion. ^II  Rates are found in many facets of life including interest rates, currency conversions, measurement conversions from one unit to another of the same type (e.g., units of length, such as feet to meters), prices of items, inflation rates or even the production rates of goods or services, and of course rates of motion.

To further expand upon the idea of proportional relationships we will first discuss the concept of constant motion and its relevance to speed and velocity. An object is in constant velocity if the displacement, both in distance and direction, traveled by the object is the same in any two equal time intervals (for example, every second, or every minute). An object is in constant speed if it travels the same total distance in any two equal time intervals. Two objects can have the same constant speed but different velocities if, for example, one is traveling around a circle and the other travels in a linear fashion. As the object that is traveling in a circle is constantly changing directions, its velocity will vary, even if it travels at a constant speed. Both velocity and speed are two metrics used to quantify changes in an object’s position per unit of time.

A reexamination of scalar and vector quantities within the context of an object’s motion will highlight the importance of this classification with regard to speed and velocity. To be ready for this, students must have mastery of basic arithmetic functions, be familiar with algebra, and have experience with ratios. This unit will heavily focus on introducing students to proportional relationships with specific attention placed on rates and ratios related to motion. In addition, students should have the capacity to translate between different schemes of graphical representations of data. We will examine these concepts in detail with respect to the following example.

A bullet train travels 600 miles northward in six hours, and then reverses direction for 3 hours, traveling 300 miles south. What is the train’s average speed and average velocity?

The average speed of an object is determined by the total distance traveled in a given amount of time. Thus for every hour the bullet train travels a total distance of 100 miles. Alternatively, the train travels 900 miles for a total trip duration of 9 hours resulting in an average speed of 100 mph. Velocity is derived from the concept of displacement and includes direction in the description to an object’s motion. The average velocity is based on the train’s displacement per unit of time and would only include the difference between the train’s final position and initial position. Since the train reversed directions for 3 hours the train moved a total of 300 miles in 9 hours, resulting in an average velocity of 33 mph (to the nearest whole mph) northward. From the train’s original position, it moved a net direction north of 300 miles; thus the average velocity of the train would be written as 33 mph, northward.

Average speed = total distance traveled / time of travel

= (600 mi + 300 mi) / 9 hrs

= (900 mi) / 9 hrs

= 100 mi / hr

Average velocity = displacement / time

= (s _final – s _initial) / (t _final – t _initial)

= (600 mi northwards – 300 mi northwards)/(9 hrs – 0) =(300 mi – 0) / (9 hrs – 0)

= 300 mi / 9 hrs

= 33.33 mi / hr, Northwards

The tables below describe two objects traveling in constant motion at 1 second intervals of time. The object’s position, duration of travel, and displacement per unit of time is recorded. Assume that each object starts in the same position and describe each object’s motion

Object I

Object II

Table 2. Describes two objects traveling in constant motion at 1 second intervals of time. The object’s position, duration of travel, and displacement per unit of time is recorded. Assume each object starts at the same position.

When examining objects I and II from the data tables above we can see that two objects start at the same location; however the nature of motion for each object is quite different. For example, object I experiences constant speed over a period of 7 seconds; for every second the object moves 3 meters. The average speed and velocity of object I would be 3 m/s. If the movement of object I were to be graphically illustrated we would observe a linear slope, meaning that every point along the slope would represent the same rate of speed. (See Figure 3 below, left side).

When we examine object II’s motion we see an initial rate greater than that of object I. After 3 seconds object II alters its direction of motion and begins to move back towards its place of origin. Upon closer examination we can determine that object II is not traveling at a constant speed. The distances traveled in different one second intervals are different; moreover the direction of travel is also different in different 1 second intervals. The total distance traveled by object II is 28 meters out and 28 meters back, for a total of 56 meters. It does this over a period of 7 seconds. Hence, the average speed of object II is 56m/7s = 8.0 m/s, however, the speed in different one second intervals along the trip may be faster or slower since the speed is not uniform. For example, in the third second object II travels 18 meters, for a speed of 18m/s.

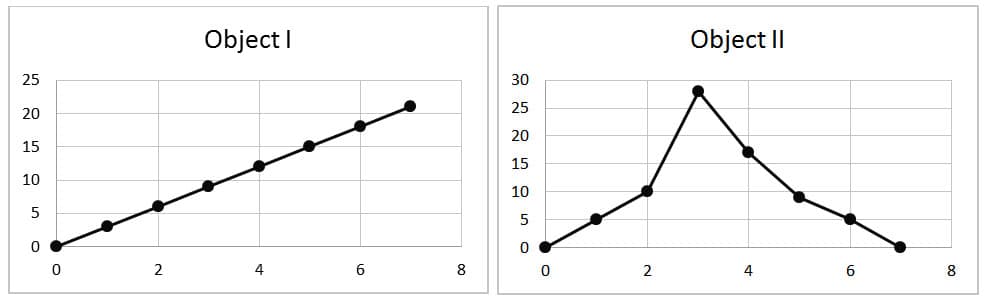
Figure 3. The position time graphs illustrate the motion of two objects. The linear slope of objects I depicts constant motion whereas object II exhibits motion at varying velocities.

Constant velocity occurs when an object travels the same distance and direction in any single unit of time. This means that in two units of time, it has double the displacement of one second, and in three seconds, it has triple the displacement, and so on for longer intervals. This means that the relation between displacement and time traveled is a proportional one. From our discussion above of proportional relationships, we know that this relationship can be described algebraically by the following equation, where velocity of an object is denoted by v, total displacement is represented by d and time is t. For constant velocity motion, the velocity is the constant of proportionality between displacement and time.

v = d/t

If for example an object moves at a constant velocity of 20 m/s for 10 s eastward, the object would be displaced 200 m, Eastward.

v = d/t

d = vt

d = (20m/s)(10s)

d = 200 m, Eastward

The equation could be transformed to calculate the interval of time, as long as the scenario explicitly states the object travels at a constant velocity. This unique relationship between time, displacement, and velocity only applies to objects that are traveling in constant motion and the same direction. If you were to plot a position-time graph that involved a constant rate, a linear slope would result. This demonstrates graphically the proportional relationship between total displacements per unit of time in the case of constant velocity. At every point along the slope the same rate would result meaning that the average velocity and instantaneous velocity of the object would be the same. In order other words, for every unit of time the velocity of the object would be the same.

How long does it take for a runner traveling at a constant speed of 5 meters per second to travel 1500 meters?

s = d/t

t = d/s

t = (1500 m)(5 m/s)

t = 300 s