The Unit
As someone who is proficient in math and art, I sometimes use measurement in very casual ways. If I need a 7 foot of paper to decorate my bulletin board, I go tear off a piece of paper from the large roll. I’m typically quite accurate without using a measuring tool. If I need a piece of fabric, I estimate what I need based on the width of the bolt and the lay of the pattern. When I’m cooking, I often don’t use measuring cups and spoons, unless it is vital for the recipe.
My students are rarely proficient in math and even if they are, they are likely not as adept at estimating the things mentioned above, more due to experience than understanding. In our seminar, we worked on measurement using square units. We studied polyominoes as a potentially effective device to get students to understand the concepts of perimeter, area, and volume using the most basic of units. I would like to include skills on how to use a ruler, as well, to get students to actively use their knowledge of perimeter, area, and volume in real life scenarios and begin to get that needed experience in measurement.
Rules for Rulers
Far too often, students don’t know to start at 0 when using a ruler. When there is a gap at the beginning of the ruler before 0, they don’t understand to skip it. Once a student told me that he always thought since he was supposed to skip the little gap that the teacher meant to skip to 1, so he always had. We want to dispel any misunderstandings and start with the basics of measurement with a short introduction to rulers, yardsticks, and measuring tapes that we will then use to actively measure things large and small to gain more experience. We will emphasize the idea that a number on a ruler is telling you how many unit lengths away from the zero point it is located, these units usually being either inches or centimeters.
Forms, Properties, and Units of Measurement
Forms of Measurement
There are many forms of measurement: time, weight, mass, velocity, atmospheric pressure, temperature, altitude, distance, and depth, to name a few. Even counting is a form of measurement. Then of course, there is our focus- perimeter, area, and volume. These are forms of measurement we see and use almost every day, often without even thinking about it. For a quick example, “do you want the small, medium, or large drink?” involves a measure of volume. Asking students for examples of perimeter, area, and volume will give a quick overview of student understanding of these specific forms of measurement.
Properties of Measurement
There are four key properties of measurement that we took note of in our seminar: comparison, combination, repetition, and partition. Though each is very simple, I feel that some students will benefit from going over them, others may feel more confident starting the unit with something they understand well enough, and others who thoroughly understand can be of assistance to others around them that need extra help.
1. Comparison is when we compare two quantities with respect to the same measurable attribute. This comparison can be represented as equal, unequal, less than, or greater than.
A |________|
B |__________| If A<B, A>C, and A=D, we conclude that B>D and B>C.
C |______|
D |________|
2. Combination is when two of the same form of measurement of varying amounts are combined, or added together, as seen in addition.
A |________| B |__________| A+B= |________|__________|
This may be extended to encompass subtraction, also.
3. Replication is the repeated copying of one unit of the same form of measure, a form of multiplication.
A= |________| 2A= |________|__________| 3A= |_____|______|______|
4. Partition is when a unit or group of units of a single form of measure are subdivided into equal parts, a form of division.
A= |________| A= 1/2 A + 1/2 A |____|____|
These four properties guarantee that we can use numbers to express any measurable attribute of a quantity as a certain multiple of a pre-selected unit of the same attribute. That is, we can express the length of some object as a certain number of inches, or the area of some region as a certain number of square miles, or the weight of a bag of apples as a certain number of pounds, and so forth. But for the number to have meaning, we need to specify the unit.
Units of Measurement
Units of measurement will depend on what is being measured and the tool doing the measuring. It is impossible to measure volume in degrees or temperature in ounces, perimeter in minutes or area in kilowatts. Units for length include, but are not limited to, inches, feet, yards, miles, and their metric counterparts- centimeters, meters, and kilometers. A measurement is created when a number is attached to an individual quantity by choosing a unit of measure. The width of a piece of copy paper is 8 ½ inches. The paper’s actual width is the individual quantity. 8 ½ is the number, which is an adjective to modify the noun, inches. The important thing to know is, all numbers need a unit in order to take on meaning. If you ask me how many tables there are in my classroom and I say 7, you understand I am saying 7 tables. However, if I randomly tell you I need 7, you will likely have no idea what I am talking about. Is it dollars? Pizzas? Boa Constrictors? You won’t know until I say that what I need is actually 7 pencils. Attend to the unit, it matters.
Area, Perimeter, and Volume
Area and perimeter are basic geometry concepts. However, getting students to reliably associate the name with the purpose or the equation is a bit harder than just telling them once. Perhaps a good way to explain is it in everyday terms. If the gym teacher asks students to walk the perimeter of the gym, what does she want them to do? Does she want them to walk randomly around the entire gym floor bumping into each other or does she want them to walk around the outer edge? Most students understand the teacher wants them to walk around the outer edge. As well, when the teacher asks students to clean up their areas, they generally understand it isn’t just the edges of the space around them to be cleaned, but the entire desk and floor around them that the teacher wants cleaned up (whether they actually clean it up or not). Perimeter versus area is understood in both instances, however, students may not connect these ideas to geometry concepts in math class. Volume is the three-dimensional space that something occupies, such as air. Students can easily recognize the difference between a 12 oz can of soda vs. a 20 oz bottle vs. a 32 oz drink cup at the gas station as a physical example, but may not fully comprehend the numbers associated with the containers. We will be dealing with rectangles and squares in this unit- the most basic of shapes, and whole numbers, so that students will become more comfortable with the ideas and methods presented rather than being wrapped up in algebra and fractional arithmetic.
Relation of Units of Length, Area, and Volume


Note: For irregular shapes and forms it may be necessary to decompose, or break down, the shape or form before calculating area or volume. To get perimeter of an irregular shape, simply add the lengths of every side together.
Polyominoes
“Polyominoes are the shapes made by joining squares edge to edge. They were named and first studied by mathematician Solomon W. Golomb, starting in 1953.”4 Most people know what dominoes are, though they may have been called biominoes if Mr. Golomb had named them. His work with polyominoes has changed the world forever in many ways. “He developed a game (polyominoes) that was the later basis for the later computer game Tetris.”5 Many students will immediately recognize the polyomino shapes as Tetris pieces. Golomb’s mathematical research was “regarded as vital to the digital communications revolution…His concepts known as Golomb rulers and Golomb sequences were used to make possible such digital communications as internet and cellular telephone networks.”6
Polyominoes show how complicated planar shapes can be and how simple rectangles are.7 This is why we break down complicated shapes into simple shapes to find area and perimeter. Below are polyominos up to number 6, they do however go on and on. We will only be using up to the number 6 for our unit. Students can challenge themselves by going higher.

Polyominos can be rearranged so long as every square is touching another square, edge to edge.

If each square unit is not edge to edge with another unit it becomes a separate unit.
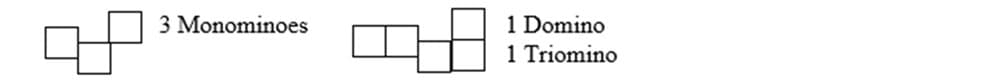
When introducing polyominoes, I will show students, one unit, then the domino and explain how it only has the one way to present it, side by side. Next, the triomino, side by side or as an L form (as seen above). Students will work together (see Polyomino activity) to find the polyominoes of the 4-unit tetrominoes (5 variations) and 5-unit pentominoes (12 variations) and present them on the board by teams.
Next, we will look at hexominoes, the six-unit polyominoes. Hexominoes will always fit into one of the six areas of an enclosing rectangle shown below.

There are 35 combinations within these enclosing rectangles. It is a challenge to find them all, and flips, rotations, and mirror images may be hard to eliminate, but do not count. It is important to note that the perimeter and area of the enclosing rectangles are different, as are the perimeters of the created hexominoes within the enclosing rectangles. Hexominoes will all automatically have an area of 6 units2 because they all consist of 6 individual unit squares. Students will investigate and find all the Hexominoes in small groups and as a class.
Hexomino Nets and Tetradic Cuboids
A net is a 2-D shape that can be folded up to make a 3-D form. Nets are also defined in geometry as “A pattern that you can cut and fold to make a model of a solid shape.”7 The area of a net is equal to the surface area of the form. Some hexominoes are nets for a cube. A tetrad is any group of four things and a cuboid is a form made by putting cubes together, in ways similar to the formation of polyominoes in the plane. When four cubes come together to create a form, where each cube must have one face completely touching the face of another cube, they form a tetradic cuboid.
Creating Nets Out of Hexominoes
Of the 35 hexominoes there are 11 that can be cut out and folded to make a cube; these are called cube nets. The challenge that will be presented may be done visually, though some individuals may need to cut out the shapes of the nets and fold them up to determine if they will form a cube or not. In the mathematics textbook, Mathematics for Elementary Students, Sybilla Beckman notes that “One important reason to study geometry is that it promotes the ability to visualize and mentally manipulate objects in space. This is a necessary skill for many professions.”8 She also mentions a report from the U.S. Department of Labor that states “being able to ‘see things in the mind’s eye’ is a foundational skill for solid job performance”.9 Students will work in pairs to discover which of the 35 hexominoes fold into cubes, as described in the Activities section. Students will each pick a cube net of their choice and recreate it.
The following are the 11 hexominoes that can form a cube.

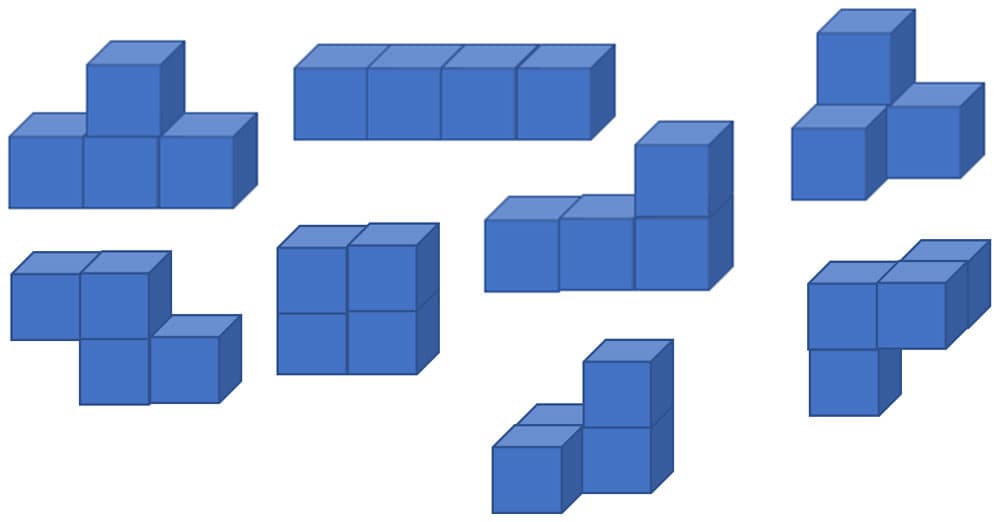
Tetradic Cuboids
When 4 students get together, with the cubes they created from their hexomino nets, they will work together to assemble tetradic cuboids. I will challenge each group of 4 students to make as many different tetradic cuboids as they can. When they make one, they will sketch it, then disassemble their cubes to make another one. These cuboids will be the models for the final product in this unit, a tetradic cuboid made of clay slabs.
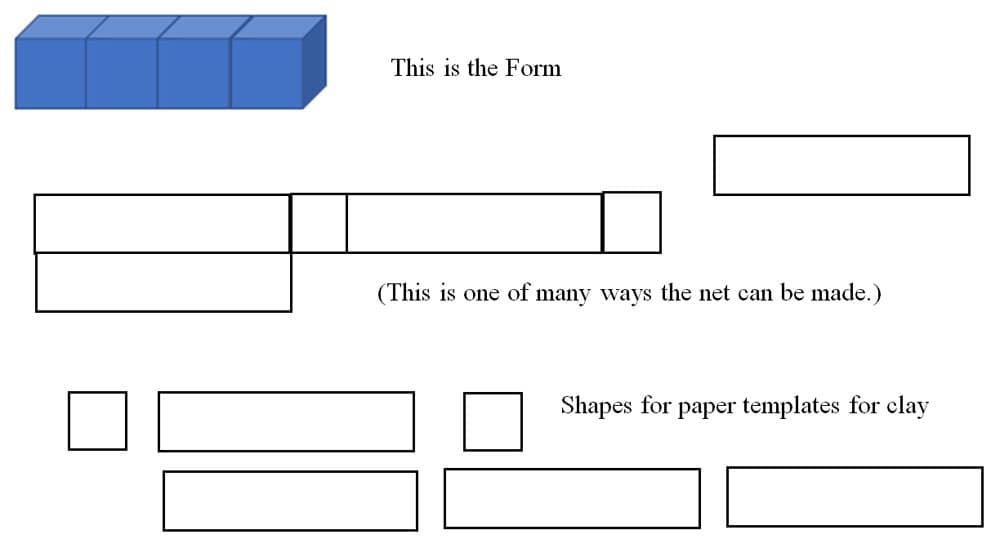
The clay slabs will be made from paper templates of the planar surfaces of the cuboids. For example, the square prism would have two 1-unit squares for the ends and four 4-unit straight slabs for the sides. If these are assembled into a plane figure in preparation for making the cuboid, the plane figure will be a net for the cuboid. Students can also create a cardstock net that will be folded and glued so they can use it as a model of the tetradic cuboid they will build out of clay.

Comments: