Titus-Bode Law - Estimations of the mean distance from the sun using Earth as a unit of 1
| Distance to Sun in Astronomical Units | |||||||
| Planets | +4 | Total | Div by 10 | Titus-Bode | Actual | Difference | |
| Mercury | 0 | 4 | 4 | 0.40 | 0.40 | 0.39 | -0.01 |
| Venus | 3 | 4 | 7 | 0.70 | 0.70 | 0.72 | 0.02 |
| Earth | 6 | 4 | 10 | 1.00 | 1.00 | 1.00 | 0.00 |
| Mars | 12 | 4 | 16 | 1.60 | 1.60 | 1.52 | -0.08 |
| Asteroid Belt | 24 | 4 | 28 | 2.80 | 2.80 | 2.80 | 0.00 |
| Jupiter | 48 | 4 | 52 | 5.20 | 5.20 | 5.20 | 0.00 |
| Saturn | 96 | 4 | 100 | 10.00 | 10.00 | 9.54 | -0.46 |
| Uranus | 192 | 4 | 196 | 19.60 | 19.60 | 19.18 | -0.42 |
| Neptune | 384 | 4 | 388 | 38.80 | 38.80 | 30.06 | -8.74 |
| Pluto | 768 | 4 | 772 | 77.20 | 77.20 | 39.44 | -37.76 |
Taking the difference between the predictions of Titus-Bode and what is know today, we see that overall, the Titus-Bode Law does a fairly good job of predicting a planet's mean distance from the sun.
We can also use another statistical concept to illustrate the accuracy of the Titus-Bode Law predictions –; the scatter or XY diagram. A scatter diagram graphically illustrates the relationship between two variables or items of interests. In this case, that would be Titus-Bode calculation of mean distance and the accepted calculation of mean distance.
The chart below is a XY diagram of our raw data –; Astronomical Units calculated using Titus-Bode and current accepted AU measurements, with a line drawn to connect the points or observations.
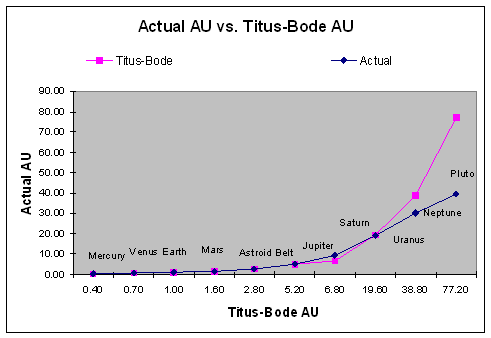
As we look at this chart, we can see that there are two somewhat bent, but almost identical lines. How strong is the relationship between these measurement systems? A statistician by the name of Carl Pearson studied this type of phenomenon and he figured out a way to calculate both the strength and direction of a linear relationship. Since we have a fairly linear relationship, we can use Pearson's product moment correlation coefficient, or r. To do this, he developed the following very famous formula.

Where
- r = correlation coefficient
- x = individual observations of a variable (Titus-Bode)
- x¯= the average of the X variables
- y = individual observation of another variable (current measurements)
- y¯= the average of the Y variables
- Sx = the standard deviation of the X variables
- Sy = the standard deviation of the Y variables
Before we attack this foreboding looking equation, it might be a good idea to review the elements that make up the equation. To do this, we need to review some of the basics of descriptive statistics. Statistics is divided into two main branches, descriptive and inferential. In descriptive, we merely describe and plot the data with no value judgments; the data is used to describe a phenomena of interest. In inferential statistics, value judgments are made. In this example, Titus-Bode vs. Actual, we will hypothesize, or make an educated guess, that there is little or no real (significant) difference between the two groups of data.
The first item that we will look at in this equation is the average or mean which is denoted by a bar over the variable such as x¯ (verbalized as "xbar"). The mean is the sum of all the variables divided by the total number of variables. The standard statistical equation for this is Σ x/n. The Greek letter sigma (Σ) in the numerator translates to "sum all"; the denominator tells us to divide by the number of observations (n). For example, if we took the height in inches of three students in a class of 25 and got 60, 65 and 70, we would add the heights together and get 195 and divide by 3 to get an average height of 65 inches.
The mean or average probably is the widely used of the statistical procedure; and it is also the most abused. Data is greatly influenced by a few or even a single much larger or smaller observation, with the result not accurately describing our collection of observations. Instead, we may want to use the median to describe the data. The median is the middle value of an ordered set of observations. In our case, the median would be 65. This is just like the median in a highway –; the middle between the two lanes going in opposite directions. If there is an even number of observations (say 6, 10, 14, 100), the middle two numbers are averaged; if the number of observations is odd, then the middle value is used. There is a final descriptive statistic called the mode, which refers to the most often, or most common, occurring value. In our example there is no mode. These three measures (mean, mode, and median) are often referred to as measures of central tendency as they describe the center of the data (or where the data tends to cluster) in a given data set.
An observation or data point is part of a set or group of data. For an observation to be meaningful, it needs a reference point and a way of measuring the relationship of that observation to that reference point. We call this reference point is the mean and our measurement is the Standard Deviation. Standard refers to the norm or what is expected (in statistics, this is typically the mean) and deviation is the difference or numeric distance that an individual data point is from the standard. To do this, we need to find the standard or mean, x¯ which we already have calculated as 65. By subtracting 65 from 60, 65 and 70 we get differences of -5,0 and +5. If we add these differences together we get 0. This doesn't do us much good. This zero problem exists anytime we get a group of data, find the mean and then subtract the mean from each item and add the differences. (Your might want to ask student to verify or "prove" this to themselves with a very simple data set.) To avoid this problem and maintain the differences, we square the differences. This is called the variance. The -5 squared is 25, 0 squared is still 0 and 5 squared is 25. We can now add theses numbers and get 50. But this 50 doesn't tells us very much so now we need to find the average difference. To do this, we divide by the number of variables. In our case n = 3 so that 50/3 approximately equals 16.7. But what does this 16.7 square inches mean? We now need to turn this number back into something that is meaningful (the original unit of measurement, or inches), so we take the square root of our 16.7 square inches, which is approximately 4.1 inches –; this is the average difference of each variable from the mean.
The statistical formula for what we have just done is:
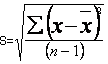
where s = the standard deviation and
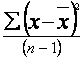 = the
variance
= the
variance
For purposes of illustration we use 3 for the denominator. In actual practice if we take a sample of data we must subtract one from the number of observations or n-1 as the denominator. Statisticians do this because of what is called the error of the mean. That is, if we take many samples of data from the whole population, each mean will be slightly different assuming we take an unbiased sample based on some random selection. Also note that the English "S". This implies a sample or a part of the population and not a census or including all members of the population. Since standard deviation is a measure of how close data is together and there is always an element of error in using samples the denominator is decreased by one. The purpose of this is to be conservative in claiming how close the data is. The smaller the denominator, the larger the quotient. Statistics always wants to error on the conservative side of analysis. A larger standard deviation will have a flatter curve while a smaller standard deviation will have a steeper curve indicating that the data is grouped much closer. If every element of a population is included in our data we use the lower case Greek sigma, F in place of s and we use N instead of n-1. In this case, we have considered only a small sample of every element, so there is an error of the mean but to simplify calculations, we used the value of N or 3.
In nature most data, when graphed, follows what the statisticians call a normal distribution or bell shaped curve. The bell shaped curve indicates that the majority of the data fall under the center of curve. The chart on the next page illustrates this normal distribution but with a slight "twist" –; it has a mean (center) of 0. The numbers along the base of the curve, ranging from -4 to + 4 represent standard deviations. Now we have combined our reference point (the mean) and our measurement of the distance from an observation to the reference point (the standard deviation).
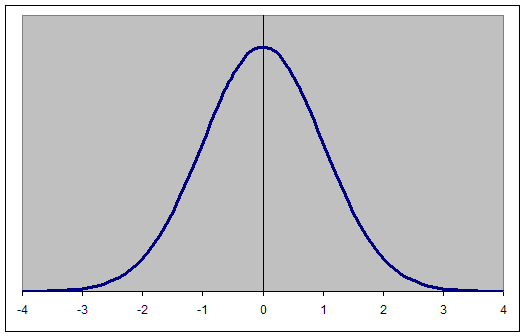
This is a standard normal distribution. The centerline at 0 represents the mean, mode and median which in normal distribution are the same (in addition, it divides the data in two, with 50% on one side of the line and 50% on the other). Data having a wider range would produce a flatter curve while data with a more narrow range would produce a more steep slope. In our example, the zero represents 65, the + 1 would represent 65 + 4 (standard deviation) or 69, and the -1 would represent 65-4 or 61. The higher and lower the standard deviation marks go the fewer the observations having that value; that is, at a -3, there would be very short people and at + 3, the people would be very tall.
The French mathematician Abraham de Moivre discovered the formula for this curve using calculus. He determined that if you add or subtract one standard deviation to the mean you capture about 34% of the area under the curve for a total of 68% of the data. A repeat of this addition and subtraction, gives two standard deviations yielding about 95 percent of the area under the curve and three standard deviations is about 99 percent of the area. Since the ends of the graph, called the tails, go on forever (infinity), there is no limit to the number of standard deviations one can calculate; therefore, 100% of the observations are under the curve. Since the exact calculation of the percentages are very complicated, we use a z or t score table to calculate the location (in percentage) of an individual score expressed in standard deviations. The calculation of a z-score is as follows:

Where
- x = the observation of interest (a specific point)
- x¯= the average of the observations (mean); and,
- S = the standard deviation of the variable x
Most every statistics text has a table for Z. By looking up the value in the columns of the table, the body of the table gives you the percentile of a given x.
So far, this discussion has been about one variable. When the discussion turns to two variables, an x and a y, there is covariance (the extent to which two variables vary from their means). This covariance becomes important when we want to calculate the strength and direction (correlation) between two variables or measurement systems. Covariance is mathematically expressed as:
Cov(x,y) = Σ (x- x¯ ) (y- y¯) /N-1
Using our Titus-Bode and Actual AU data, we illustrate this principle.

The products of the differences are multiplied and the sum of the products is then divided by (N-1) since we are using a sample and not the population and want the average. However, this doesn't really mean much or tell us a lot because we have not standardized it. To do this, we must consider the standard deviations of the two variables (and brings us back to our original express of the correlation coefficient, or r).
The table below is an insert from an Excel worksheet that manually calculates the standard deviations of our two variables (Titus-Bode or x, and Actual or y). I often have student do a similar worksheet manually to get the basic idea of how the calculations are done manually before having them work calculators and spreadsheets.
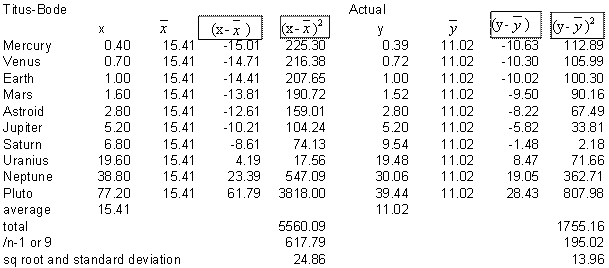
The product of the two standard deviations is (24.86)(13.96) = 347. Dividing the covariance by the product of the standard deviations or, 333.12/347 yields and r = + .96
A correlation coefficient can only take on values between -1 to +1. This value gives us the strength (the number: the higher the number, the stronger the relationship) and direction (the + or -) of the relationship between our two variables or measurement systems. In our example, r = +.96 , a strong and positive relationship. Had our ratio turned out to be a + 1, there would be perfect correlation, meaning that the measurement systems were identical, and the a graph would show the two lines atop each other. As the ratio goes from + 1 to 0 there is less strength between the two until at 0 there is no relationship. Below 0, the strength of the relationship is reversed. In such a case, one variable increase as the other decreases. For example, from birth to about age 20, we get taller; this is a positive relationship. If the coefficient is zero, then there is no correlation; the scatter diagram looks like a circle of dots (an example might be finding the relationship between brown eyed people and I.Q). A negative correlation is illustrated by the fact that after the age of 40 we tend to shrink or as we age passed 20, our height decreases.
Calculating r can be done many ways. Using a TI83 hand calculator, press Clear and then clear memory by pressing the "gold" key and then the "mem" key located at the + sign, press 7 (reset), press 1 (all ram),press 2 and then press the enter key twice. Press the "stat" key and then the "edit" key. This brings up a spreadsheet. Key the x variables in column 1 and the y variables in column 2. Variables may be entered in other columns, but the calculator uses these two columns as the default. Press "gold" key and then the "quit" key to get a blank screen. You must now activate "diagnosticOn" . To do this, press the "gold" key and then the "catalog" or 0 key. Either scroll down to "diagnosticOn" or, since you are in the alpha mode, press the "d" or "x - 1" key to get to the d's and then scroll down to the "diagnosticOn" key and press enter. Press the "stat" key, use the right arrow to go to "calc" at the top of the screen and enter 4 or "LinearReg (ax+b). Voila, you should see y = ax + b, a = .539, b = 2.67, r 2 = 92 and r = .96. So if you wish to graph the best-fit line to our data, you have y = .539x + 2.67. Our "r" is the same as we manually calculated above. But we now have r 2 which should be R 2 . This is the square of little r or .96*.96 or .92. R 2, though not needed here, is the measure of the amount of variability in one variable explained by another variable. In English this means that little r tells us that there is a very strong relationship between the two variables 96% and R 2 tells us 92% of Titus-Bode explains Actual astronomical units.
In Excel, the calculation is much easier. Go to "Tools" on the toolbar and open up "Add-ins" to see if "Analysis Toolpack" is installed. If not, check the box and it will self install on most current releases of EXCEL. Enter the two columns of variables on a worksheet and grab them in a rectangle with the mouse. Go to "Tools" and press "Data Analsis", highlight "Correlation Coefficient" and answer the questions. You might also use the "Descriptive Statistics" option. Set up and the first time use can be frustrating, but once used, subsequent uses are quick and easy. On all these automated systems, patience is rewarded.

Comments: