Strategies and Classroom Activities
Drawing Free-Body Diagrams
The objectives demonstrate the process involved in the analysis of any object in static equilibrium. After demonstrating to the students how to draw a free-body diagrams I will have the students work in pairs at two desks moved together to draw free-body diagrams from a worksheet. Each group is given handouts with eighteen diagrams of objects in different physical situations from which they must draw and label the free-body diagrams. They will first draw the free body diagrams on large (two feet by four feet) white boards. The large white boards allow me to circulate in the room and help students on an individual basis, the students are not permitted to move to the next free-body diagrams until I have checked their board. Students in this situation can be self-paced and with the partner have discourse about their diagrams. The students will copy the correct free-body diagram onto their worksheet to have a permanent record of the picture and the free-body diagram just like in figures 1 and 2 above. To summarize the activity a discussion will follow to find the similarities and differences in the different situations. I want the students to recognize that the free-body diagram for a weight hanging from a wire is the same as a book at rest on a table except the book is in compression and the wire is in tension. There are many of these similarities in drawing free-body diagrams.
The next step will be to have students develop free-body diagrams not from drawings or pictures of the physical situation, but from written descriptions of physical situations. For example the student will start with the following description of a physical situation: A student pushes on a desk with a force of 50 Newtons at an angle of 30 o and the desk does not budge. Draw and label the free-body diagram. The student must use the textual clues to develop the free-body diagram. For example the word budge means the desk is in static equilibrium and the sum of the forces must equal zero. Then they must conclude that when "a student pushes on the desk" there is resistive force acting on the desk that is not clearly defined. That resistive force is static friction. When using word problems as opposed to diagrams, the solutions can vary from student to student. For example one student will draw the student pushing to the right and in a downward direction (the 30 o angle above the horizontal) and another might draw the force from the left and pushing upward (the 30 o angle below the axis). The lack of detailed information in the above example can lead to different interpretations of the problem. There will be class discussion on how word problems of this type can be interpreted differently and how the free-body diagrams would differ but the process of determining a solution would be the same.
Vector addition strategies
Graphical analysis
Students will practice the graphical analysis of vectors addition using rulers and protractors. Initially, I will model graphical analysis as direct instruction in a whole group format. As a group we will step through a problem, setting the scale, drawing each vector to scale in a head to tail fashion and determining the solution by drawing and measuring the vector from the tail of the first vector to the head of the last vector. The student will then practice a problem independently, and again as a homework assignment. Students generally do not have difficulties with the process of graphical analysis of vectors. Their problem arises with making the scale either too large or too small. A few students need extra help with using the protractor and understanding what is meant by a direction in the form of, 50 o East of South. Students will get frustrated with the graphical addition because the time commitment to make a scaled drawing. That leads to teaching the mathematical method of vector addition.
Mathematical addition of vectors
Prior to the unit on Newton's Laws and forces the students have been taught how to resolve vectors into their horizontal and vertical components using right triangle trigonometry. Therefore the only new skill to develop in this unit is how to sum the vertical and horizontal components. The free-body diagram is vital in this process. The student must examine the free-body diagrams to add and subtract all the components of the forces in the horizontal direction and then set that sum equal to zero. They will then repeat the same process in the vertical direction. If the free-body diagram is not correct then the formula developed from this diagram will be incorrect. The equations of static equilibrium developed will then be solved using algebraic techniques for any unknown forces. The ability to analyze a free-body diagram in to a mathematical relationship is the most difficult skill in the introductory physics classes; therefore the students must practice the skill repeatedly.
Bridge Building
The purpose of the bridge building project is to help students practice the analysis of a real structure in static equilibrium. The students will design and build a bridge and apply their knowledge of how to analyze forces to determine the forces in one portion of their bridge structure. The dimensions of the elevated bridge will be 35 centimeter long, 15 centimeters above the ground level and 5 cm wide. Each student must draw a scaled drawing of their proposed bridge structure which reinforces the same type of skills as graphical analysis of vectors. I will introduce the inquiry bridge building project by showing a power-point presentation of various bridge designs. The power point will show a truss system, an arch support and a suspended bridge design. In each system we will discuss how the forces are transferred from the bridge deck to the ground support. Students will have to limit their model design to a trussed bridge constructed from dry pasta and glue to limit the materials that must be made available. Dry pasta will be used because it is inexpensive, available in various sizes, such as spaghetti, linguine, fettuccini, and lasagna for the road bed and requires no tools to cut. In addition to the scaled drawing the students will have to show the free-body diagram for a section of their bridge and determine the force in each member for a given load of 100N. Upon completion, the bridges will be tested for their mechanical efficiency. The mechanical efficiency of a structure is the ratio of the mass the structure can support compared to the mass of the structure.
To determine the forces in each member of a truss panel, instruction on how to sum the torque or moment around a point must be accomplished. The students will do a numerical solution to the bridge project and a graphical solution. To begin a numerical solution the students must draw a free-body diagram of one panel of their truss bridge design as shown in figure 6, below.
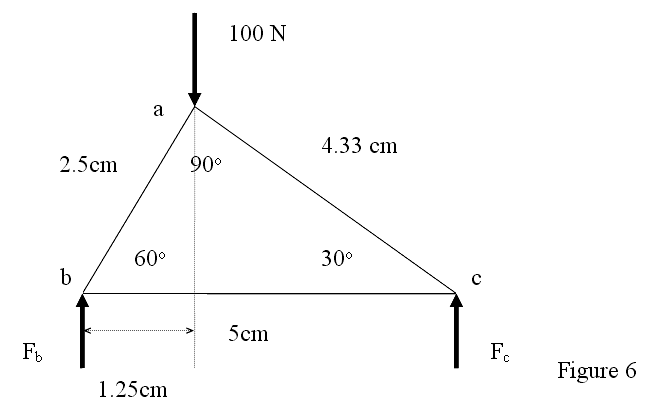
We will begin the numerical solution by finding the sum of the torque, which is the product of the force and the moment arm, around point b and setting it equal to zero. The result will be the following:
∑Τ b = 100N(1.25cm)-F c(5.0cm) = 0
Solving for F c = 25 N
Next the students will sum the forces in the vertical direction and set the sum equal to zero to find F b the result will be the following.
∑Fy = 100N - 25 N - F b = 0
Therefore F b = 75 N
It is customary to begin finding the forces in each member of a truss at the left reaction point F b in figure 6. We begin by drawing the free-body diagram of joint b as shown below in figure 7 below. Also shown in the figure are the sum of the vertical forces to solve for the force in the ab member and the sum of the horizontal forces to solve for the forces in the bc member of the truss. The solutions are F a b = 86.6 N and F b c = 43.3 N.
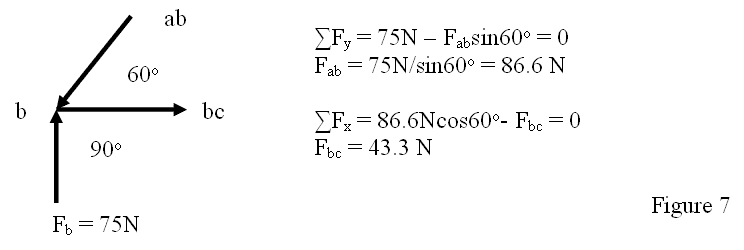
An identical process would be followed for the c point on the truss panel to solve for the force in the ac member or we can solve for ac member at the point a. The free-body diagrams and the force equation for the c point are show in figure 8 below.
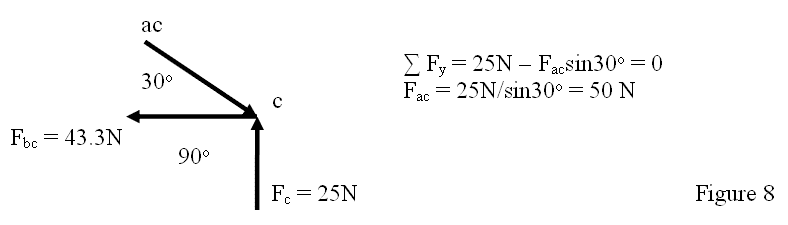
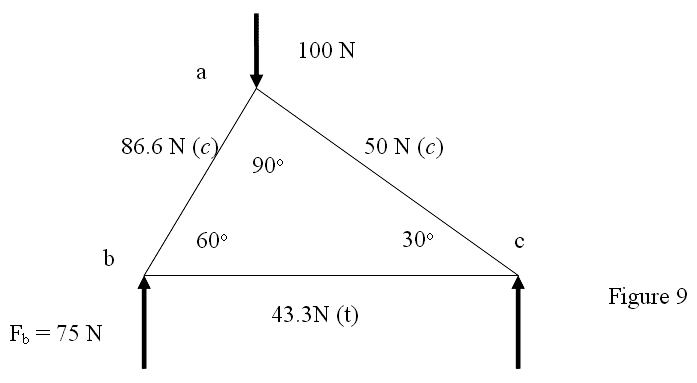
The final summary diagram that shows all the forces on and within the truss panel is shown in figure 9 below. A compressive force is indicated by a (c) next to the magnitude and a tensile force with a (t). 2
In a final discussion of the student's bridge analysis, I will ask the students the following questions about the forces in the members of one part of their bridges based on their free-body diagram analysis. Which members are in tension and which are in compression? Which members have the most force in them and the least amount of force and why? How can you change the material you use to optimize the design of your bridge?
When the models are complete, they will be tested for the mechanical efficiency by loading the bridge on the road bed until failure occurs. Then, in a final discussion that includes a power point of pictures of truss structures other than bridges, such as buildings boat, and airplanes. The class will have a whole group discussion about the connection between the bridge structure and analysis of other structures in the world.

Comments: