Appendix B: Extended Scope and Sequence
Number Bonds to 10
My students come to second grade with a large deficit in their understanding of the relationships between numbers contained in what we usually refer to as "fact families." I think it is important to concretely show students the relationship between the numbers in a fact family. "How are 7, 3 and 4 related? Can you show me with a picture?" When we start to represent the relationship between the members of a "fact family," we are dealing with pictorial representations called "number bonds." It is the manipulation of these number bonds that will help our students see and remember the connection between the numbers in a fact family.
What is ten?
Very young children in the United States are not taught to understand that our number system is based on a decimal notation. They are not usually taught to appreciate what "base-10" means until about 2 nd grade. I feel that this is entirely too late to introduce such an integral and fundamental explanation of our number system. 13
I start my math curriculum by focusing on what a digit is because this is the foundation for later knowledge of place value and order of magnitude. I explain that there are ten digits (0,1,2,3,4,5,6,7,8,9) that we combine in a variety of ways to represent any number we can imagine. I further explain that the way in which we arrange these digits holds meaning. I reintroduce the digits from our decimal system with a picture of the value they represent.

I then show the students a number of counters pictured on the overhead. They have to choose the correct symbol to represent that number, and once we agree, we write the digit on the board. I do this with many quantities of counters from 0-9.
Once the class seems familiar with the digits, I show them ten counters. I ask them how they would write this number using the digits. I often ask, "Is there a digit for this value? Can we write this number using just one of the digits?" When they answer, "No!" I take this opportunity to explain that in our decimal notation system we love to work with groups of ten. "Working with groups of ten is easy. 10 is a very round number, which makes it easy to deal with. Adding something to zero is simple because any number plus zero leaves you with the number you started with (n + 0 = n). Zero doesn't ask us to change anything. When we get a full group of ten, it deserves a higher ranking, so we bundle that ten together and call it by a new name. Instead of having ten single items, we now have 1 group of ten." I then explain that this is how we "compose a ten", and we show that we have one ten by putting the digit for one in the tens place on a tens and ones chart. "This is how we communicate that we have one group of ten." Then I ask, "But do we have anything else to count? Are there any counters left over after we make a ten?" When they answer correctly, I assert that since there aren't any counters left we need to account for that in our number, so we write a 0 in the ones place to show that we have made one group of ten and have no extra pieces left to count. I can also ask, "If we didn't write the zero, how would we know that we are talking about 1 ten and not just 1 one?"
I would then have them break into pairs to quickly practice this with amounts from 0-10. Partner A puts a number of counters into the ones place on a "Tens & Ones" chart. Partner B counts the counters and decides if they represent a one-digit number or a group of ten. If the counters equal 10 then Partner B must pick up all of the counters and put them in a cup. The cup is then moved to the tens place on the chart. If he or she is correct, they switch roles and continue to play. This may seem like a very low level activity for second graders, but I feel like it is extremely worth investing the small amount of time it would take to have this discussion and practice the process.
Composing and Decomposing 10
The foundation has now been laid for further exploration of how to compose a ten. The lessons taught in the first quarter are focused on giving the students the opportunity to compose and decompose 10 in a variety of ways. The goal is that the students be able to readily retrieve all the possible ways of combining single-digit numbers to equal ten. I want them to see 2 and automatically know that if you added 8, you would be able to compose a ten. Conversely, I want them to think that if they started with ten and needed just 6, they would have to break apart that very round number into 6 pieces and 4 pieces. There are a number of activities that you can do to reinforce the composition and decomposition of a ten.
One such activity involves displaying 10 beans in a variety of combinations on popsicle sticks. Each child gets 5 popsicle sticks, and they are asked to glue a1 bean on the left side and nine small beans on the right side of the stick, leaving a space in the middle. For example, the popsicle sticks might look like this, where the 0's are beans.
| Model of Popsicle Stick | Number Bonds Represented |
| 0 000000000 | 10 = 1 + 9 or 9 +1 |
| 00 00000000 | 10 = 2 + 8 or 8 + 2 |
| 000 0000000 | 10 = 3 + 7 or 7 + 3 |
| 0000 000000 | 10 = 4 + 6 or 6 + 4 |
| 00000 00000 | 10 = 5 + 5 |
This is a visual representation of a number bond. They can physically see that 1+9=10. Furthermore, if they flip the popsicle stick around, they see the commutative property of addition in noticing that it's also 9+1=10. They will do this with 2 and 8, 3 and 7, 4 and 6, and 5 and 5. The sticks can be saved in bags for further explorations.
Another way of reinforcing the composition of 10 is to use Cuisenaire rods. They are measured in cm and are in lengths from 1 unit to 12 units. Therefore, you could have each student measure each different colored rod with a cm ruler and have him/her mark on the rod how long it is. The students could then be prompted to find all of the combinations of rods that are equal length to the 10 rod. This might look like this:
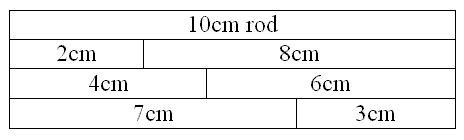
There are many more activities that one can use to increase student confidence in composing and decomposing ten. I want to stress how important this skill is as a building block for later understanding.
Number Bonds to 20
Once the students can readily compose and decompose a 10 (noting that I will use these terms alongside of "make" and "unmake"), they will be ready to move to addition and subtraction facts to 20. It does not make sense to teach students to just rely on the "count on" and "count back" methods in adding and subtracting to 20. This does not instill in them an appreciation for the efficient system that is decimal notation. Instead, it implies that our mathematics is without a logical system for communicating numbers, when in reality our system is very sophisticated.
One possible way to avoid deficits created through just counting on and counting back, is to emphasize that the numbers from 10-20 are composed of one ten and a number of ones. For example, 17 should automatically be seen as one ten and seven ones. We can help young children internalize this view (for immediate retrieval) by consistently pairing the combined digits with the expanded form of the decimal notation and a visual representation. This may look like the following:
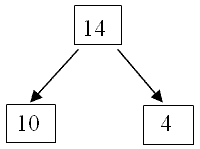
If we are consistent in showing this triplet in the same ways/forms then we are helping our students see the "teen" numbers in a more useful and meaningful way. The development of this perspective is pertinent because it gives students a uniform view of the logic of our decimal notation system. You may want to draw their attention to the illogical way we name the numbers from 11-19 in English. We call 1 ten and 1 one eleven. It would make more sense if this was called "tenty-one" because it would follow the pattern set later with "twenty-one" or "fifty-one," for example. It would also be helpful to try to point out how to hear the "ten" in "fourteen." "Can you hear the "ten" in 14? It sounds a little funny, but it's there at the end. So, "four-teen" means we have four more than ten, and if you listen carefully, you can hear the "four" and the "ten." This would have to make accommodations for the number names of 11, 12, 13 or 15. For example, in "fifteen" neither the "five" nor the "ten" are obvious in the word "fifteen."
To reiterate, if we only began to talk about "regrouping" when we deal with numbers larger than 20, we do not give any recognition to the structure of the decimal notation system. And thus, we end up with children who are confused and unable to successfully perform higher-level addition and subtraction computations. In an attempt to counteract this, we will spend a large amount of time doing "teen" computations with the decimal notation system in mind. We will continue to compose and decompose a 10 whenever necessary. The process may look something like this,
14 + 6 = (10 + 4) + 6
We can now see that we can work with 4 + 6 first.
So, 14 + 6 becomes 10 + (4 + 6) and 4 + 6 = 10
14 + 6 = 10 + (10)
The new 10 plus the original 10 from 14 is equal to 2 tens or 20.
14 + 6 = 20
When we start to represent familiar numbers as a sum of its parts, then it becomes easier to look at all the possible relationships. We could look at 17 in a variety of ways. It could be 10+7 or 11+6 or 12+5, etc. The ability to see the teen numbers in this way will give students the opportunity to approach problems from many points of reference. They could solve 17-9 by thinking first that 17 = 10 + 7. They could then proceed to do 10 - 9 = 1, and then 1 + 7 = 8. Or a child might see that 17 = 9 + 8. They then would easily recognize that they could just subtract that 9 and be left with the 8, so they would successfully solve 17 - 9 as equaling 8.
Exploring Multiples of 10 and Order of Magnitude
Towards the end of the 2 nd quarter focused on doing these sorts of activities with numbers to 20, we will begin to look at multiples of 10 up to 100. Now that the students can compose and decompose a 10 readily and are strong with facts to 20, we can then begin to explore expanded notation and order of magnitude. I think a logical activity to start with is to concretely explore the relationship between a single digit number and a multiple of 10 with the same leading digit.
We will start with 20, since we at this point we are focused on all computations dealing with numbers up to 20. I will talk about 20 in reference to the way we discussed 10. We will compose and decompose 20, using base 10 blocks as a way to see the actual bundling and breaking apart of the 2 groups of 10.
It is now that I will also introduce the idea of multiples of 10. We will talk about 20 as being ten times bigger than 2. We will see a quantity of 2 alongside a quantity of 20. I will ask, "Which group looks bigger? Do you know how much bigger this group is? It's ten times bigger than the group of 2!" We will then proceed to split the 20 pieces into 10 groups of 2. (This is an opportunity to also reinforce counting by 2s.) In this way, they will see that if you have ten groups of 2 items, you have 20 things. We will then talk about 3 and 30 in the same fashion, making the point that 30 is 10 times bigger than three. We will continue this with 40 and 50. I have chosen to stop at 50 at this point for three reasons. First, looking at five multiples of ten should be enough to establish a pattern. Second, I don't want to explore the concept of 100 equaling ten 10s until I have laid a stronger foundation. Third, we are going to make centimeter rulers that measure up to 50 centimeters, and this activity will be a perfect compliment to the idea that 10 is 1 ten, 20 is 2 tens, 30 is 3 tens, 40 is 4 tens, and 50 is 5 tens.

Comments: