Background
I read dozens of articles about Number Sense before formulating my own working definition of it. I break it down into three major categories: Number Systems, Mathematical Operations, and Flexibility in Mathematical Situations. The Number System refers to recognizing different types of numbers, place value, relative magnitude of numbers, and different representations of them. Mathematical Operations encompasses addition, subtraction, multiplication, division and the relationships between them. It also includes understanding the effect of these operations on different types of numbers, and the Rules of Arithmetic that govern operations. Flexibility in Mathematical Situations is the ability to recognize multiple ways to work with numbers/data and identify the most efficient method with which to proceed. It also includes the ability to recognize the reasonableness of answers and when an answer requires an estimate versus an exact answer. 4 Gaining flexibility in mathematical situations is really the ultimate goal of this unit because it is what will allow students to perform mental arithmetic.
Number Systems
I think nearly every high school math book begins by identifying and naming sets of numbers. There are the Natural (or Counting) numbers starting at one and increasing forever. Whole numbers are the Natural numbers and zero. Integers are the set of all Whole numbers and their opposites, so now we have positive and negative numbers. Simply put, Rational numbers are all those that can be written as a fraction (i.e. a quotient of two integers). Since Integers can be written as a fraction with a denominator of one, or in any equivalent form, they are included in the set of Rational numbers. Irrational numbers are all other Real numbers than cannot be written as a fraction. Well known examples are π and Sqrt(3). The Real numbers consist of the Rational numbers together with the Irrational numbers. Real numbers can be represented as points on the number line. When students reach Algebra 2 or Precalculus they learn about Complex numbers that are comprised of a real and an imaginary component, and Complex numbers can be represented as points in the plane.
Students with good number sense recognize multiple representations of numbers - pictures, symbols, graphs, or number lines can be used to represent numbers - and there are multiple symbolic ways to represent a number. For example, the symbols 3/2, 1.5, 1x1/2, and 1 + 5/10 all represent the same number.
Place value
We spent a considerable amount of seminar time discussing the remarkable characteristics of our base 10 number system. It is a compact method in which whole numbers are represented as sequences of digits, and the position of each digit determines its value. Students can identify the hundreds, tens and ones places in a three-digit number; however, as Roger Howe said, the names for the positions are often treated merely as vocabulary words. We considered a progression of representations for the expanded, or decomposed, form of numbers. Initially, young students decompose the number 532 into 500 + 30 + 2 showing the value of each digit. Later, students recognize place value as powers of ten. Each "single-place number" can be written as a digit-times-a-power-of-10, and any number can therefore be written as the sum of digits-times-a-power-of-10. For example, 745 can be written as the sum: 745 = 7x100 + 4x10 + 5x1 which becomes 7x10x10 + 4x10 + 5x1. For my high school students who have experience with exponents and scientific notation, each single place number can also be written as a digit-times-a-power of ten in exponential form. Thus, 745 = 7x10 2 + 4x10 1 + 5x10 0. The pattern of decreasing the power of 10, going from left to right, continues for numbers having decimal places; the number 45.16 can be written as 4x10 1 + 5x10 0 + 1x10 - 1 + 6x10 - 2. Decomposing numbers in this way, will illustrate to my students why 10 0 is defined as one, and why, according to the Laws of Exponents, negative exponents represent reciprocals (i.e. 10 - 1 = 1/10 1 and 10 - 2 = 1/10 2=1/100). Expanding decimal numbers in terms of reciprocals of powers of 10 also illustrates the relative size of each place value. In this form, I can emphasize to students the fact that the fraction 1/10 is larger than 1/100 because they both have the same numerator, but the fraction with the smaller denominator represents a larger number because the "whole" is being divided into fewer, and therefore larger, pieces. In fact, 1/100 is only 1/10 of 1/10. It's not that I think my Precalculus students don't understand place value, but I'm sure they have not discussed it in many years of math classes, and they have not explicitly written numbers in expanded form using exponential form, or what they have learned in science classes as scientific notation. I think practice in decomposing numbers in this way will help them internalize the meaning and size of numbers.
Number Line and Order of Magnitude
The next stage in building number sense is getting a feel for the relative size of numbers. For smaller numbers, the number line can connect quantity and measurement. This idea was also discussed in our seminar. In order to visualize the relative size of place values, the first step is to define one unit on the number line as the distance between zero and one. Then the number two on the number line is twice that same distance from zero, and the number ten is located ten times that distance from zero; the distance from zero to 100 is 100 times longer than one unit and also ten times longer than ten units. The distance between zero and one can be divided into ten equal spaces to show tenths on the number line. A meter stick is a number line that illustrates the relative sizes of three orders of magnitude: 1 meter = 10 decimeters = 100 centimeters = 1000 millimeters (the smallest marking on the stick).
The power of ten determines the Order of Magnitude of a number; each order of magnitude is related to the next by a factor of ten. Some familiar scales report only the Order of Magnitude. The numbers on the Richter scale, describing the magnitude of earthquakes, are the powers of ten. A magnitude 7 (=10 7) earthquake is actually ten times stronger than a magnitude 6 (=10 6) earthquake. On the pH scale, a solution with pH = 3 is 100 times more acidic than one with pH = 5. Likewise, decibels are the powers of ten used when measuring the intensity of sound. These are all logarithmic scales (pH is a negative logarithm), which I can use as examples of applications for my Precalculus students. I present more Order of Magnitude problems in the Activities section and in the sample problem sets in Appendix C.
Mathematical Operations
Once students are adept at expanding numbers based on place value, they can operate on them. They can add and subtract using the process they previously learned as "combining like terms." The "like terms" are those that have the same place value! They will add each place separately. Since each place contains a single digit, the addition proceeds quickly and easily. Even in cases that require regrouping, students at this level should not feel the need to use a calculator. As an example, to find the sum of 4,289 and 5,176, the first step is to expand each number: 4289 = 4x10 3 + 2x10 2 + 8x10 1 + 9x10 0, and 5176 = 5x10 3 + 1x10 2 + 7x10 1 + 6x10 0. To find the sum, we add like terms: (4x10 3 + 5x10 3) + (2x10 2 + 1x10 2) + (8x10 1 + 7x10 1) + (9x10 0 + 6x10 0). Then, the sum becomes 9x10 3 + 3x10 2 + 15x10 1 + 15x10 0. We recognize that 15x10 0 (aka 15) must be rewritten as 1x10 1 + 5x10 0 making the tens place 16x10 1 (aka 160), which in turn is rewritten as 1x10 2 + 6x10 1. Our final sum becomes 9x10 3 + 4x10 2 + 6x10 1 + 5x10 0, which is put back together as 9,465. At first this process may seem cumbersome, but as Roger Howe told us repeatedly, "Shortcuts are the privilege of the expert." It is well-worth spending the time to reinforce understanding of place value and require students to expand the single digit numbers so they can move towards mental calculations. In fact, I would expect students to add two or three 2-digit numbers mentally by adding the digits having the same place value.
Within the above example for finding the sum of two four-digit numbers, there is a perfect opportunity to address some of the Properties of Arithmetic, namely the Associative and Commutative Properties of Addition, and the Distributive Property of Multiplication over Addition/Subtraction. (All nine Rules of Arithmetic are defined in Appendix B.) Students have been taught these properties, but typically in isolation, so they have very little carryover for when they might be useful. Once each number was written in expanded form, combinations of the Commutative and Associative Properties allowed us to rearrange the terms to place like terms next to each other and group them together. Although, it wasn't illustrated precisely the way textbooks state it, the Associative Property allowed us to group the like terms to work with them as four pairs of sums. It is the Distributive Property that allowed us to combine the like terms to form a single term with the same power of 10. When adding 4x10 3 + 5x10 3, what we actually did was factor out the common factor of 10 3 which gave us (4 + 5)x10 3. We then performed the arithmetic in parenthesis, giving us 9x10 3.
We perform subtraction the same as addition, using the expanded form of multi-digit numbers. We subtract single place numbers with the same power of 10. If we need to borrow, we convert one unit of the next higher place value, to make 10 units of the place that needs it, since the next place to the left is ten times larger than the given one. For example, to find the difference between 17.2 and 9.8 we begin by writing each number in expanded form: 1x10 1 + 7x10 0 + 2x10 - 1 - 9x10 0 - 8x10 - 1. Rearranging and regrouping, we get 1x10 1 + (7x10 0 - 9x10 0) + (2x10 - 1 - 8x10 - 1). We will need to borrow twice (1x10 1 = 10x10 0 and 7x10 0 = 6x10 0 + 10x10 - 1), so the difference becomes 0x10 1 + (16x10 0 - 9x10 0) + (12x10 - 1 - 8x10 - 1) which is equal to 7x10 0 + 4x10 - 1, or 7.4. Later, in the Flexibility section of this unit, I will discuss methods that would make such a subtraction problem easier to do mentally, without pencil and paper. However, as mentioned earlier, students with good number sense need to be flexible in their mental calculation strategies, and there will be times that it is simplest to subtract single digit numbers place by place.
We can also perform multi-digit multiplication by expanding each number into its single digit components and multiplying each component from one number by each component of the second number and adding the resulting products. Essentially we are applying the Distributive Property multiple times. For example, multiplying a two-digit number by a three-digit number requires using the Distributive Property twice: (a + b)(c + d + e) = (a + b)c + (a + b)d + (a + b)e = ac + bc + ad + bd + ae + be. This process can be extended to any size numbers, and leads to what Roger Howe and Susan Epp refer to as the Extended Distributive Property, or the "Each with each" rule. 5 In practice, however, I find it easier to set up the multiplication as we did in the seminar, using a grid to ensure I don't miss any products. I will demonstrate the process by finding the product of 482 x 736. First, expand 482 = 4x10 2 + 8x10 1 + 2x10 0 and 736 = 4x10 2 + 8x10 1 + 2x10 0. Next, label three columns of a box with the components of 482 and label three rows with the components of 736, as shown below. (The Commutative Property of Multiplication allows us to multiply in any order, so there is no significance to putting 482 on the top and 736 on the side; they could be reversed.) Using what is called an area model, although the boxes are not drawn to scale, multiply the two "dimensions" (base = 4x10 2 + 8x10 1 + 2x10 0 and height = 7x10 2 + 3x10 1 + 6x10 0 ) to compute its area. The total area of the shaded region is the composite sum of all nine individual shaded boxes.

Notice that all of the multiplications involve only single digits, meaning students only need to know their basic multiplication facts from one to nine. Also, notice that like terms can be found on diagonals going from the lower left to upper right of the box. Thus, grouping like terms can be done quickly; the product of 482 x 736 = 28x10 4 + (12+56)x10 3 + (24+24+14)x10 2 + (48+6)x10 1 + 12x10 0. After simplifying, the product becomes 28x10 4 + 68x10 3 + 62x10 2 + 54x10 1 + 12x10 0. To finally get the number in standard decimal form, we do regrouping. Regrouping five times from right to left, we get 3x10 5 + 5x10 4 + 4x10 3 + 7x10 2 + 5x10 1 + 2x10 0, or 354,752. This area model method can be applied to any number of digits, whether the two factors have the same number of digits or not. While I would not expect my students to multiply two three-digit numbers without paper and pencil, I would expect them to be calculator-free.
This multiplication example presents the opportunity to reinforce more Rules of Arithmetic - the Commutative and Associative Properties of Multiplication, as well as the Extended Distributive Property (aka "Each with Each" rule). The Distributive Property appears as the "Each with Each" rule, and then again when we sum the terms involving a given power of ten. In each box we arrange the four individual factors so we first multiply the single digits together and then multiply the powers of ten together. In the process, we are also demonstrating the Law of Exponents - when multiplying the same base (in this case the base is 10), we add the exponents. In other words, if we multiply 10 2x10 1, we are multiplying ten twice and then once more for a total of 10 3. The fact that this does not depend on the way the factors of 10 are grouped, only on the total number of factors, is another instance of the Associative Rule.
Since I am not allowing students to use calculators for this, multi-digit multiplication is a perfect opportunity to practice estimation to check the reasonableness of their answer. Performing the product of just the largest place value from each number gives us 4x10 2x7x10 2 = 28x10 4 = 2x10 5 + 8x10 4 = 280,000. Therefore, the order of magnitude of the estimated product and the actual product, 354,752, are both five. Estimation, along with the amount of error relative to the actual number, will be discussed in more detail in the Flexibility section.
There is a strong connection between multi-digit multiplication using the expanded form of a number and multiplication of polynomials. For students that have already studied algebra, the next example demonstrates the connection between algebra and arithmetic. If I convert the product of 482 x 726 into a polynomial in x, the product becomes (4x 2 + 8x + 2)(7x 2 + 2x + 6). This product can be computed using the area model, also:

Looking at the diagonals, we can combine like terms to get the product: 28x 4 + 68x 3 + 62x 2 + 54x + 12. Then, if we replace x with 10, this becomes the same product as the previous arithmetic example. Thus, students have been multiplying polynomials since elementary school; it's just that the variable always had a value of ten! I have taught students how to multiply polynomials successfully using the area model/box method. I think they will appreciate the connection between algebra and basic arithmetic, and it will take away some of the mystery of working with variables.
Operating on Rational Numbers
So far, my multiplication examples have used only whole numbers. Young students spend a great deal of time learning arithmetic with whole numbers that are all greater than one. As a result, many believe that multiplication always makes things bigger. Likewise, they believe that division makes things smaller. These generalizations must be replaced when they study rational numbers. Recognizing that operations have different effects on different types of numbers (i.e. multiplying natural numbers versus rational numbers) is a critical understanding within number sense.
To convince students that multiplication does not always make things bigger, I will present them with counterexamples such as 600 x 0.2. To find the product, we can rewrite each number showing place value: 6x10 2 x 2x10 - 1 = 12x10 1 = 1x10 2 + 2x10 1 = 120, which is clearly smaller than 600. Multiplying multi-digit numbers containing decimal fractions can be done in the same way as whole numbers, with the area model/box method. To find the product of 654 x 0.55, first expand each factor and calculate the product (6x10 2 + 4x10 1 + 3x10 0)?(5x10 - 1 + 5x10 - 2):
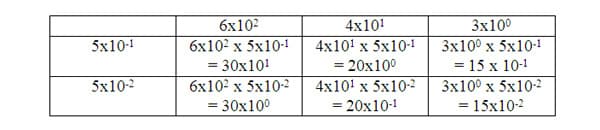
Combining like terms on the diagonals, we get 30x10 1 + 50x10 0 + 35x10 - 1 + 15x10 - 2. Regrouping to get single digits times a power of 10, the product becomes 3x10 2 + 5x10 1 + 3x10 0 + (5 + 1)x10 - 1 + 5x10 - 2 = 353.65, which is, again, less than the starting number, 643. The next question becomes, how accurately do we need to know the product? If we were doing scientific calculations, and needed a high degree of accuracy, we would use a calculator. However, for typical everyday calculations, an estimate is probably sufficient.
Another characteristic of number sense is understanding the relationship between operations. When algebra students learn to solve equations, they learn to use inverse operations. Addition "undoes" subtraction and vice versa; therefore, they are inverse operations. Multiplication and division are also inverse operations. This concept can possibly be used to help students understand the "flip and multiply" algorithm they learned for dividing fractions. If x=a/b÷c/d, then, multiplying (the inverse of dividing) both sides of the equation by c/d gives us c/d•x = a/b. (A division problem is the same thing as a missing factor problem – something I will discuss with my students to ensure they understand it.) To solve for x, we would multiply both sides of the equation by the reciprocal d/c, which gives us (c/d •d/c)x = (1)x = a/b•d/c. Thus, setting the two expressions for x equal to each other, a/b÷c/d = a/b•d/c, we see that dividing by a fraction is equivalent to multiplying by the reciprocal of that fraction. 6 Another way to think about this process is in two steps: first divide by c, and then divide by 1/d, which is the same as multiplying by d. (These steps can be done in the reverse order because of the Commutative Rule for Multiplication.) Students that understand both processes will gain flexibility in manipulating expressions. Students can reinforce this process by working practice problems using inverse operations with numbers in place of the variables.
Flexibility in Mathematical Situations
The third major characteristic of number sense is having flexibility in mathematical situations. It involves recognizing when it is appropriate to estimate an answer and when a more exact answer is needed. It involves checking answers to determine whether they are reasonable. Flexibility is also the ability to consider multiple strategies and select the one that is most efficient for the situation. I think that learning and practicing techniques based on number sense will ultimately lead to improved confidence in performing mental arithmetic and less reliance on a calculator.
Estimation and Relative Error
In the first multiplication example I presented (482 x 736), I estimated the order of magnitude of the product to be five (10 5) by multiplying only the first digit (highest order of magnitude) from each number. By the same method, the order of magnitude of the product of the last example (643 x 0.55) is two because 6x10 2 x 5x10 - 1 = 30x10 1 = 3x10 2. In our seminar, we calculated relative error in terms of the desired quantity and discussed how the number of digits used in a calculation determines the accuracy of the answer. To calculate Relative Error, we use the formula E = |Q' – Q|/Q, where Q is the desired answer and Q′ is the calculated answer. In the previous example, we can calculate the relative error as E = |300 – 353.65|/353.65 = 0.15 = 15%. In many everyday cases, 10 - 20% error is acceptable. If we were to use the first two digits and multiply the highest place value of each number with the first two digits of the second number (i.e. the 3 boxes that make up the upper left corner in the area model), we would get a product of 3x10 2 + 5x10 1 = 350. The relative error would be reduced to E = |350 – 353.65|/353.65 = 0.01 = 1% which would definitely be acceptable for everyday use.
We considered the effect of estimating answers to the first one, two and three digits of a number. The "worst-case" for estimating with only the first digit is that the estimate has 50% error. The worst case occurs when the first digit is one because if the actual number is very close to two, the ratio of the difference to the actual is 1/2. For example, estimating the number 199 as 100 gives relative error as E = (199 – 100)/199 = 0.497 ≈ 50%, meaning we know at least half of the actual number. If we use the first two digits to estimate, the error is reduced to a maximum of 10%, meaning we know at least 90% of the actual number. Estimating with three digits gives at most 1% error, meaning we know at least 99% of the actual number. Therefore, when doing mental arithmetic, it is typically not necessary to carry out long multiplication problems; they can be estimated with a high degree of accuracy using the two, or at most three, single digits with highest place value in each number, even though the relative errors from each estimate are additive. Depending on the group of students, I may demonstrate how to calculate relative error, and lead a discussion about what is acceptable error in different situations.
Mental Computation Strategies
Lastly, I would like some of the activities in this unit to teach my students mental computation strategies that they may never have been taught formally. I want to build their confidence in performing arithmetic so they no longer feel the need to rely on a calculator. The strategies described below come from the book Number Talks: Helping Children Build Mental Math and Computation Strategies and from multiple articles about performing mental calculations.
Partitioning
Partitioning, in one sense, is decomposing numbers according to place value, as described earlier, and performing operations on them place by place. Partitioning makes addition and subtraction of two 2-digit numbers quite simple to do mentally. For example, to add 54 + 36, we add 50 + 30 = 80 and 4 = 6 = 10, then 80 + 10 = 90. To subtract 54 – 36, we do 54 – 30 = 24, then 24 – 6 = (24 – 4) – 2 = 20 – 2 = 18.
Even adding 3-digit numbers, or beyond, can be simple. For example, to add 116 + 118, 116 can be partitioned into (110 + 6) and added to (110 + 8). The sum becomes (110 + 110) + (6 + 8) = 220 + 14 = 234, which can be performed mentally. For younger students, partitioning can also refer to breaking a number apart to "make a ten." Using the same example, 116 + 118, 116 can be partitioned into (110 + 2 + 4) and added to (110 + 8). The sum becomes (110 + 110) + (2 + 8) + 4 = 220 + 10 + 4 = 234. The 'trick" was recognizing that 2 + 8 makes a ten, and the six ones in 116 can be partitioned into 2 + 4.
Doubling and Halving
Most people can double numbers easily in their heads. Looking for doubles and then adjusting as needed is another strategy that can be applied to find the sum of 116 + 118. If we double 116, we get 232, and can adjust for the 118 in the problem by adding 2 to get the sum 234. The actual thought process was probably (100 + 100) + (16 + 16 +2) = 200 + 32 + 2 = 234.
For multiplication and division, doubling numbers and cutting them in half is relatively simple for students. Therefore, dividing by four could be done mentally by halving twice. Likewise, multiplying by 8 can be done by doubling 3 times.
Adding Up
"Adding up" works for both addition and subtraction when students understand how the two operations are related. For 116 + 118, start with 116 and add 100 (from 118) to get to 216. Then, add 10 (also from 118) to get 226. Next, partition the remaining 8 as 4 + 4 to add up to 230 and then 234. To use the same strategy for subtracting 123 - 59, begin at 59 and count what you need to add to reach 123. So, 59 + 1 = 60, 60 + 40 = 100, 100 + 23 = 123. Therefore, 123 - 59 = 1 + 40 + 23 = 64. In the process, I used benchmark numbers (60 and 100) that are multiples of 10 because they are easy to work with. Some students may choose to count backward when subtracting, but the idea is the same.
Adjusting to Create an Easier Problem
Sometimes it is beneficial to adjust the problem slightly to make it easier and then adjust for it at the end. For example, to find the difference 123 - 59, I could change it to 123 - 60 = 63, and add 1 to compensate for adding 1 to 59, so the difference is 63 + 1 = 64. Sometimes I have to think about whether I should add or subtract the 1 at the end. To make the decision, I look at just the ones digits to determine what the final answer should have in the ones place. I see 13 - 9 = 4, so I was correct to add the 1.
Compensation/Constant Difference
The compensation method allows us to shift an entire subtraction problem. It is a horizontal translation on the number line, maintaining the same difference between the numbers, but making the subtraction simpler (i.e. no borrowing required!). For example, 6002 - 2537 can be rewritten as 5999 - 2534 = 3465 by subtracting 3 from each number; the difference remains the same but there is no need to borrow as you subtract the digits with the same place value.
The compensation method can be applied in many different ways. We practiced another form of Compensation in our seminar that is a bit more challenging, but interesting, nonetheless. The process is to line the numbers up vertically, and then subtract the smaller number from the larger number in each place. This step leaves a zero in each place for one of the numbers. Next, "group" the top number into multiples of 10 and subtract within each group to find the difference.
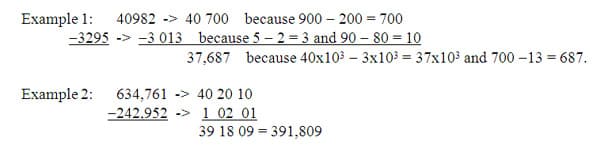
Making Friendly Numbers
Similar to making tens for addition, it is sometimes possible to make friendly numbers for multiplication. For example, the product of 15x8 can be thought of as 3x5x2x4. By applying the Commutative and Associative Properties of Multiplication, the factors can be rearranged and recombined to become 10x12 or 6x20 to simplify the multiplication.
Partial Products
Partial Products is essentially a way of using the Distributive Property. The area model/box method demonstrated earlier is an example of finding partial products by place value and adding the pieces back together. When working with smaller numbers, it is possible to do the products and addition mentally. The product of 15x8 can be thought of as (10 + 5) x 8, giving 80 + 40 = 120. I hope my students will find it feasible to multiply two two-digit numbers using partial products. The area model for multiplication shows that multiplying two 2-digit numbers involves four partial products. Not all students will be able to organize this computation mentally, but some probably will enjoy doing so. Again, starting with the product of the tens will give the largest term. Then the products of the ones from each factor with the tens from the other gives the next in order of size. Finally, adding on the product of the ones will give the complete product. Thus, 43 x 27 = 800 + (60 + 280) + 21 = 800 + 340 + 21 = 1140 + 21 = 1161.

Comments: