Strategies
My strategies consider Epp's and Howe's advice to explicitly teach place value concepts, and integrate with this the teaching of the operations addition, subtraction, and multiplication. The unit will cover four strategies. In part one, "naming numbers differently," the objective is to emphasize place value in number names. This will aid students' place value understanding and help when expanding numbers into values. Part two, "addition of multidigit numbers," emphasizes importance of place value by using expanded forms of multidigit numbers when combining numbers. The addition strategies will use the expanded form to combine like place value terms. Part three, "subtraction of multidigit numbers," continues with expanded form and combining like terms but finding the difference in values. Finally, part four, "multiplication of single and multidigit numbers," builds upon the prior strategies and expanded form to continue the focus on place value in operations. The four strategies are introduced systematically to build on students' prior learning. Some of the introductory concepts may not require full coverage depending on students' prior knowledge.
Naming numbers differently and expanded form of compacted numbers 3
American culture falls into a category of cultures whose language characteristics do not lend well to understanding place value. Students write and say numbers that do not clearly show the value presented. As an example, the English word twelve tells us no information about its value of one ten and two ones. The compacted form of 12 does show the value positionally, but if positional notation is not well developed it may cause confusion. The example of fifty-seven gives more information because we hear fifty and seven, but the value of five tens and seven ones is not obvious, more can be done to show the places and values in 57. To enrich the learning of early place value, I will first spend time constructing a better understanding of the number names by teaching the conceptual place value and calling it "place value name" similar to the name given in Chinese based languages. Chinese based languages have a name for numbers that clearly represent the place value in the name. For example, twelve would be stated as "ten two," which corresponds to the positional 12 and the value of one ten and two ones. Also, fifty-seven in Chinese is stated as "five ten seven" representing the 5 tens and 7 ones related to the positional model of 57. This name will give students an understanding of real value not just the name for a number.
At the same time the instruction of "place value names" is being explained, students can begin to see the numbers as addition of place value components. For 12, the underlying ten plus two can be shown with a number model of expanded form of 10 + 2 or 1 x (10) + 2 x (1). The expanded form shows how the digits are positioned to create the numeral of 12. The value of 1 ten and 2 ones positionally is 12. The many names for numbers can be charted to show relationships across one number, 12. The expanded form is showing each digit times a value of ten, and the "place value name" always states the largest value first. The chart below is a tool to show the connection between numbers and place value concepts.
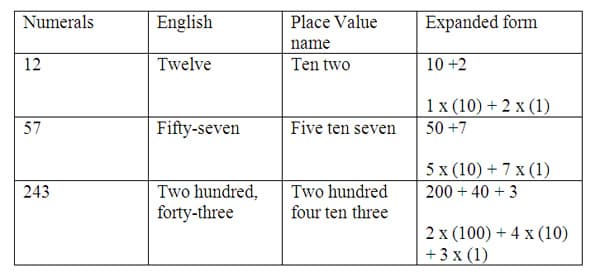
The naming of numbers many ways strengthens the understanding of their values, and also different ways to represent numbers. In later strategies students will use the knowledge of place value in singular numbers to perform operations.
Addition of multidigit numbers 4
Part one emphasizes the verbal importance of place value name as a tool to make place value parts noticeable in multidigit numbers. This strengthens overall positional understanding as it relates to place value, and simultaneously prepares students to transfer the knowledge of expanded notation to the operations of multidigit numbers. After students have practiced expanded notation of numbers, performing addition in a way that makes explicit use of the expanded notation is a natural step. Addition of multidigit numbers is traditionally taught by stacking the addends by place values in columns. We first add the values in the ones place, and then move left. If an exchange of ten is needed it is usually shown above the next column as a dash, one more. This process continues in an analogous way to the left across each increasing place. This method is efficient but does not teach the understanding of addition as a combination of values by each place. The following strategies for teaching addition are focused on both the operation and place value to give meaning to a procedural algorithm.
As described above, the expanded form of a number shows it as a sum of values corresponding to each place. The places are then put in sequence from largest to smallest value with an addition symbol between each place value (i.e. 123 = 100 + 20 + 3, or 1x100 + 2x10 + 3x1). Given an addition problem, rather than possibly blindly proceed through the 2-column algorithm just described, students can make use of the expanded form and combine "like" terms by adding the same place values together. As an example, if a problem asks students to solve 7,451 + 3,245 the strategy to place both numbers into expanded notation of (7x 1000) + (4 x100) + (5 x 10) + (1) and (3 x 1000) + (2 x 100) + (4 x 10) + (5) emphasizes place value position. It does not matter what place value the addition starts with because the sum will remain the same once all parts have been combined. The "any which way 5" rule from addition shows the sum is the same regardless of which place values are combined first. This strategy gives students more ways to solve the addition problem and deepens understanding about addition as a combination of values. The flexibility of adding any place value removes the restriction taught in column addition of always starting in the ones place. If the single digit is shown multiplied by the place value the addition can be simple by combining the single digits of the two addends (see the table below.) In this example, the thousands place shows 10 x 1,000 and this requires a trade of 10 thousands to 1 ten thousand.
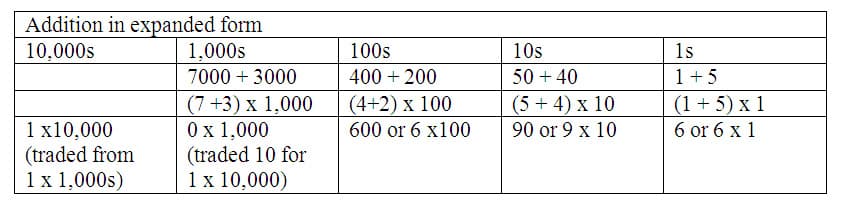
For example, 7,451 + 3,245, traditional methods add from the ones place to the left. Traditional methods start with adding the ones (like the 2-column algorithm described above), but with the "any which way" rule, any place value can be added first. For example, if I chose to start in the thousands, or even the tens place, as long as all place value sums are combined to the total, it remains the same. Therefore, if students are taught a strategy that reflects the fact that "any which way" works to find the sum, they will have a better operational and place value understanding.
One can also perform multidigit addition in a similar way using any of the expanded forms mentioned previously. I plan to have the students work through different examples of expanded forms to add to flexibility.
Tools for teaching place value and multidigit addition
Teaching different strategies to solve multidigit addition problems can be supported with tools. Two tools that are useful are digit cards and number trains. Digit cards are index-card sized cards with the values 0,1,2,3…,9, and 10,20,30,…,90 written on them corresponding to the "ones" place and "tens" place respectively. Higher places (hundreds, thousands, and so on) are represented on cards similarly. A nice aspect to digit cards is that they can be used to show a number in expanded form and compacted form. The digit cards allow the student to see numbers as expanded form when each place is represented on the card and compacted form when placed down next to each other from largest value to smallest with each card slightly overlapping that to its left (obscuring zeros). Another tool that is useful is to make number trains to represent addition in a linear model. The train uses rods of different lengths to represent ones, tens and hundreds numbers to show addition. Both tools show representations of numbers in relationship to place value.
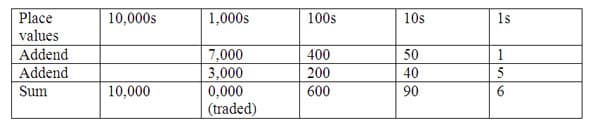
Digit cards can be used to show addition of multidigit numbers and allow for manipulation. To use digit cards as an example, 7451 is represented by the four digit cards 7000, 400, 50, and 1, which when laid next to each other left to right indicate expanded form. Digit cards can also be used to add multi-digit numbers. The problem of adding 7451 + 3245, for example, can be shown by combining place values in groups: the 7000 digit card is grouped with the 3000 digit card, the 400 digit card with the 200 digit card, the 50 digit card with the 40 digit card, and then the 1 digit card with the 5 digit card. The place value digit cards can be combined in any order, highlighting the fact that addition can be performed in any order. Once left with these pairs of cards, students can exchange the pairs for a single new card reflecting their sum. Here, students exchange for cards showing 6, 90, 600 and 10,000 (where in the last case, the sum 7,000 + 3,000 was exchanged for a higher place value card, 10,000). Placing the new cards down starting with the highest value will recreate the correct sum of 10,696 (see table below).
A different strategy to show addition using place value is a linear model that involves making number trains. This can be done using flat rods to represent 100, 10 and 1. I use a meter stick to represent a 100s rod, a "base ten long" as a 10s rod, and a "base ten cube" as a 1s rod. These last two objects are often found in classrooms. They are flat rods measured so that 10 "ten cubes" lined up left to right are the same length as a "base ten long", and 10 "base ten longs" are the same length as a 100s rod. Any objects with these same proportional relationships can be used. Roger Howe describes trains as lining up rods to represent addition of multidigit numbers. Trains allow children to see the sum value in the addition problem as two smaller values combining to make one greater value. The train starts with the first addend rods and adds the second addend rods. For example, given the addition problem of 147 + 366 one creates a number train by taking one hundred rod, four ten rods, and seven ones and creating a linear train. One then adds on three hundreds, six tens, and six ones. Next, combine like terms by reorganizing the train by placing all the hundreds together, all the tens and all the ones. This shows that the arrangement does not change the total sum while emphasizing the need to group like terms. Once the rods are grouped by place value, trade ten of any rods for one of the next greater value. For instance, trade ten ones for one ten, or ten tens for one hundred, as needed, and recreate the train with the regrouped model. The example below is not to scale but shows a representation of how the numbers can be organized in a train.
147 as a train

The next step is to show the train 366 added on, 3 hundred rods, 6 ten rods, and 6 one rods. Then rearrange both 147 and 366 to have all the hundred rods together, all the ten rods together and all the one rods together. So placing 1+ 3 hundreds rods, 4 + 6 tens rods, and 7 + 6 ones rods together. The next step is to regroup the rods with 10 or more. When this step is done I will have 4 hundred rods, 10 ten rods, and 13 one rods. I now must regroup and trade. The train then is reorganized with 7 + 6 ones which trades for 1 ten and leaves 3 ones. The 6 + 4 tens now have 1 more from the ones trade for a total of 11 tens. This 11 tens will trade for 1 hundred rod and leave 1 ten rod. The hundreds now have 1+ 3 plus the 1 traded for 4 total hundreds. The new train after regrouping has 5 hundreds, 1 ten and 3 ones. The train strategy can be shown in the written model below.

These strategies for adding multidigit numbers are ways to show addition by "grouping like terms", that is, decomposing numbers into their place value components and then adding together "like" place value components. These strategies all connect back to the traditional compact form used in the 2-column addition algorithm but unpack the place values in each number to support conceptual understanding of place value and combining values. The exchanging done in these expanded form problems is a foundational concept but one that continues to be reinforced in all the strategies.
Subtraction of multidigit numbers
Subtraction is the inverse relationship to addition. The act of decomposing (as described above in addition) in subtraction is more challenging for students specifically when borrowing or trading is needed. However, similar place value concepts and strategies can be used, and students can work though the same problems modeled in addition (using place value) above. These things show a connection between operations and will therefore hopefully be familiar to students.
Starting with a problem not requiring a trade will show the process of finding the difference of single digit numbers in the place value. Expanding the form of the compacted numbers in a subtraction problem is the first step to combining like values to see the numbers as individual places. . For example, 375 – 124 expands to 300 + 70 + 5 and 100 + 20 + 4 or (3) x 100 + (7) x 10 + (5) x 1 and (1) x 100 + (2) x 10 + (4) x 1. To show the subtraction, each single place can be subtracted and then multiplied by the appropriate place value, (3 – 1) x 100 + (7 – 2) x 10 + (5 – 4) x 1. After the subtraction is completed the remaining number is (2) x 100 + (5) x 10 + (1) x 1, which in compacted form is 251.
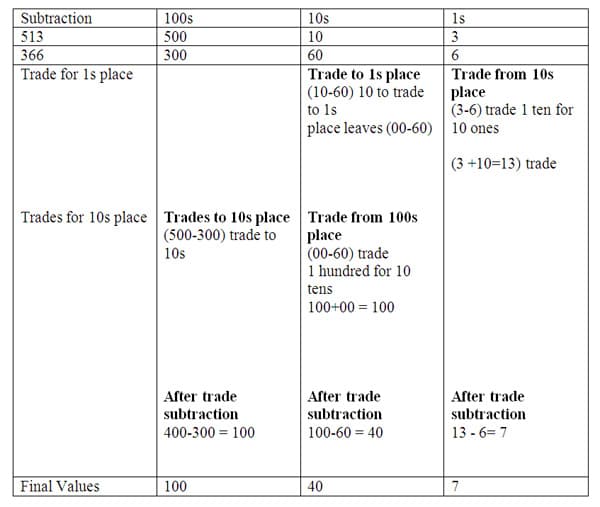
Subtraction that does not require borrowing or trading, like the example just given, is traditionally easy for students to perform using the standard 2-column subtraction algorithm. Once trading or borrowing is needed, errors tend to follow. As a model, the problem 513 - 366 requires trading. However, if students have already performed the related addition problem (366 + 147) using decomposition into place value numbers, an inverse relationship between addition and subtraction can be shown, and should lead to a clearer understanding. In the related addition problem (detailed in the previous section) two trades occurred, so it seems important to point out two trades will happen in the subtraction operation. The expanded form of 513 is 500 + 10 + 3 and of 366 is 300 + 60 + 6, or 5 x (100) + 1 x (10) + 3 x (1) and 3 x (100) + 6 x (10) + 6 x (1). Combining like values shows (5 - 3) x 100, (1 - 6) x 100, (3 - 6) x 1. Because we cannot subtract 6 ones from 3, this problem needs an exchange of 1 ten to 10 ones. This is similar to the addition problem at the stage where we had to trade ones for tens. Now the subtraction of 13 – 6 is possible and 7 ones remain. The next step is to move to the tens place, 0 tens subtract 70; realizing a trade is also need to solve. Next, move 1 hundred to the tens as 10 groups of 10 tens plus the zero tens makes 100 – 60 = 40. The hundreds place now has one less hundred and contains 400, solve 400 – 300 without a trade has 100 remaining. The subtracted values of 100, 40 and 7 are now compacted to show the difference in the two values is 147. It is beneficial to show this subtraction side by side with the related addition of 147 + 366 so the trading can be seen in both models.
Tools for teaching place value and multidigit subtraction
The tools for supporting subtraction strategies are number trains and number lines. The strategies can be shown using the same rod train model used in addition and the number line can be used to visually show subtraction. The trains are set up similarly to addition, the first number (the minuend) is laid down first, next the number being subtracted (the subtrahend) is placed below it. This creates a visual model of showing the space difference between the two trains as the difference between two numbers. The next example, number lines follows a similar model. A number line is a horizontal line marked with a "zero" and a "one", placed to the right of zero. With this, every other integer can be placed on the number line. For example, the number 2 is placed to the right of 1 at the same distance 1 is from 0. The number 3 is placed to the right of 2 at this same distance, and so on. The minuend is found first on the number line, then the subtrahend is located. The student uses the number line to find the difference in numbers with the support of the manipulative.
The train model for subtraction uses a linear model to represent the subtraction algorithm. Since subtraction with regrouping is a challenge, two digit numbers will work best in the model strategy. For example the problem 54 – 28, first create the minuend, 54, linearly and then place the subtrahend, 28, below. The missing value, or difference, is the space between the two numbers. For example, if the subtraction problem 54 – 28 is given, create a linear train of 5 tens and 4 cubes with base ten blocks or rods (as described previously), and a second consisting of 2 tens and 8 cubes, placed immediately below the first. This model shows subtraction as the difference in the two values. With this positioning, students will see that there are not enough ones available to subtract 8 from 4, and an exchange of one ten is needed in the train representing 54. After exchanging a ten for 10 ones, the "minuend" now has fourteen ones from which 8 are to be subtracted. This exchange should be recorded on the written model just as with addition when trading occurs. The next step is to find the difference between the remaining four tens and two tens, and to show the solution as 26 (see figures below).
Train representation of 54-28

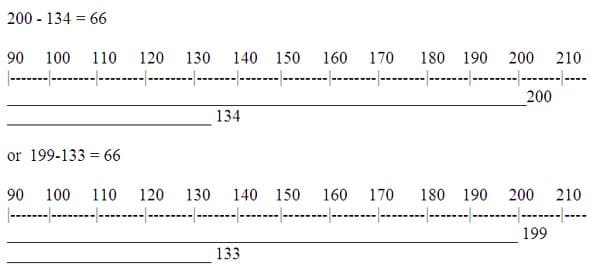
Another error prone subtraction problem involves "borrowing across zeros" to solve a problem. For instance, a problem like 200-134 is often the most challenging for students learning how to subtract with trading. The problem is due to multiple trades needed from the hundreds place to the ones place. Traditionally we would move to the hundreds place and redistribute the 1 hundred as 9 tens and 10 ones. A better strategy may be to use a number line or linear model to show 200-134. The number line is a useful tool for the subtraction algorithm and when "borrowing across zeros." Use a number line and find 200 and mark it, next find 134 and mark it. The number line can be used to see the difference between the two numbers as the space between the point marked 134 and the point marked 200. Subtracting with the number line can also sometimes be used to illustrate how to avoid trading or borrowing. The difference of the two numbers is traditionally found by subtracting the smaller number from the larger number to find the difference in the numbers. The difference between the numbers does not change if we move each number back one space on the number line, which corresponds to subtracting 1 from each. In this example, this translates to 200 – 134 = (200 - 1) – (134 - 1) = 199 – 133. Because we made the same change to both numbers the original difference 200 – 134 is still the same as the resulting difference 199 - 133. Compensating for both numbers by subtracting one from each does not change the difference, but it does make the subtraction easier because it does not require any trading or borrowing. Students can finish the problem by subtracting 3 ones from 9 ones, 3 tens from 9 tens, and 1 hundred from 1 hundred, for a total of 66. Some students may not be able to make the conceptual connection that shifting the numbers back one place on the number line does not change the difference between the values, but it shows how multiple zeros can be made into an easier problem. This strategy of compensation shows subtraction as difference and gives flexibility to solve problems.
Number line model
Multiplication of multidigit numbers
Multiplication of multidigit numbers is introduced in third grade and a standard in fourth grade. Multidigit multiplication is built on single digit multiplication knowledge. First, I will introduce strategies to students for single digit multiplication and build on the strategies and extend the strategies to multidigit multiplication.
Single digit multiplication
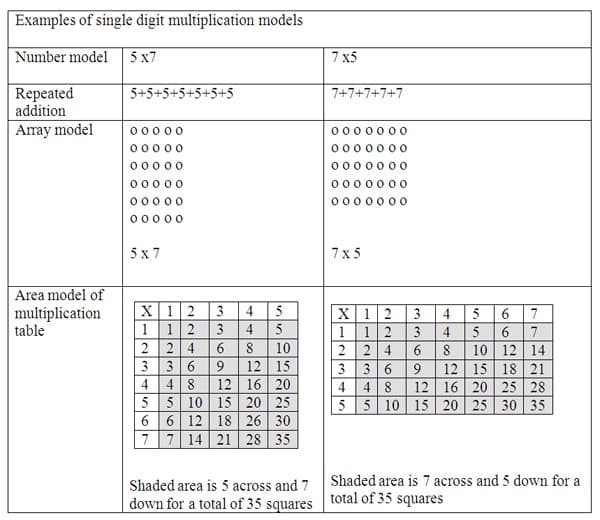
Multiplication of single digit numbers is the first introduction to the multiplication algorithm. Multiplication of whole numbers can be interpreted as repeated addition. The link to addition for student can be used in strategies to unpack the total value in a number model. I find it valuable to give multiple examples for each number model. For instance, the number 5 x 7 is the same as 5 sevens. Also, the strategies for multiplication of single digits can be shown with an array model. An array model arranges counters or items in rows and columns. For example, 5 rows of 7 counters, or 7 rows of 5 counters both make an array of 35 counters. The multiplication table itself can also represent an array of boxes or an area model. Students can use a multiplication table to cover with counters or shade over the numbers to show the area of 5 x 7 by shading 7 rows across and 5 columns for a total of 35 squares. This can be seen in the table below. Multiple strategies leads to flexibility and also deeper understanding of the multiplication concept.
Multidigit multiplication extended single digit
I will introduce extended fact multiplication strategies after single fact multiplication models are understood. At first I will introduce strategies that can be taught as extensions of single digit multiplications. These types of problems will involve multiplication with "single place numbers" such as 10,20,30, and so on. For example, the extended fact problem of 5 x 70 should be connected back to the original single fact of 5 x 7. The connection should be made to the similarity and difference between 7 and 70. The digit is the same, but the place value is different. A model would be comparing 5 x 7 as five groups of 7 ones (for a total of 35) and 5 x 70 as five groups of 7 tens (for a total of 350). The link between the single digit multiplication and the extended fact is ten times the original fact. This can be illustrated multiple ways. For example, written in expanded form 5 x (7 x 1) can be compared to 5 x (7 x 10), where the difference between (7 x 1) and (7 x 10) is visible. One can also use the associative property of multiplication to rewrite 5 x (7 x 10) as (5 x 7) x 10, so that again the difference between this number and the single digit multiplication (5 x 7) is visible. This example allows a mental math advantage of seeing the original fact and multiplying by the place values presented. Students can recall most 1 through 9 facts, and can then apply this knowledge to extended fact problems along with place value concepts. By breaking the numbers into single digit values and place values the multiplication can be seen as two parts, the single digit multiplication and place value multiplication. The final step of multiplying the single digit by the place value makes the numbers easier to work with for the student because single digits are often known and multiples of ten are easy to work with for students. Another example, the extended form can also extend both original facts by 10, for 5 x 7 extended both facts to 50 x 70. The numbers are expanded to (5 x 10) x (7 x 10) and moving numbers through the commutative property to create easier combinations, of (5 x7) x (10 x 10). The original facts combine (5x7) and then the place value factors of 10 x10= 100 creating (5x7) = 35 and (10 x10) = 100, and then make 35 x100 = 3,500. The practice of finding the single digit multiplication and then the place value multiplication are manageable with mental math and support place value concepts.
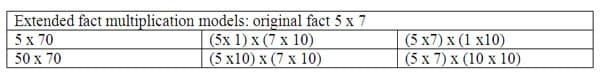
A connection here can be made to the addition "any which way rule." Multiplication has the same rule; order of multiplication does not change the product. For example, I can multiply 5 x 70 as (5 x 7) x 10 or (5 x 10) x 7, and any way I multiply will find the same product. The expanded form of the multiplication problem can be combined any which way works best for the problem solver. For example, I might use an example like 50 x 70, and first illustrate that this is equal to (50 x 10) x 7 = 500 x 7 = 3,500. I might then move the numbers to a new position of (5 x 7) x (10 x 10) to show that this same product equals 35 x 100 = 3,500. The expanded form of a number shows place value importance, while it applying single digit multiplication.
Multidigit multiplication
The next level of multiplication is a multidigit number that is not a single digit extension (like the examples above) such as 325 x 4. I will start with three digits by one digit multiplication. First, expand 325 to 300 + 20 + 5. All place value parts of 325, 300 + 20 + 5, are multiplied by 4. I then have to solve 300 x 4, 20 x 4 and 5 x 4, but the "any which way rule" allows me to chose the order in which I solve. I prefer to move from ones to hundreds and from hundreds to ones as it reinforces the any which way rule. I prefer to write the multiplications to be performed in a vertical table as follows:

The next step is to add the resulting products: 1,200 + 80 + 20 = 1,300
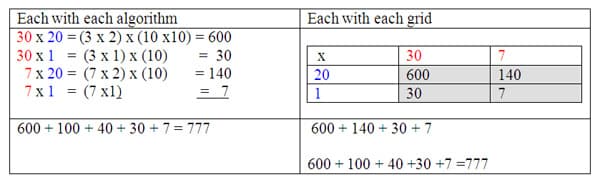
Another algorithm that is place value focused and also practical for computation is to consider each factor in a multiplication problem as a "team". An example problem is 37 x 21. Each factor 37 and 21 can be separated into place value parts, or teams of numbers (30 +7) x (20 +1). The next step is to multiply both expanded numbers with the other factor's members, that is to perform multiplication of each expanded value with the expanded value in the other factor. The strategy indicates 30 needs to multiply by 20 and 30 needs to multiply by 1 and that 7 needs to multiply with 20 and with 1 (see table below). Because this can be confusing I like to color code each number with colored pencils so as not to mix up which digits need to be multiplied. For example, I would color 30 + 7 red and color 20 +1 blue and state that you do not multiply numbers of the same color, and instead explain that each number of one color team has to be multiplied by both terms in the other color. This example shows the expanded form of both numbers and the multiplication of the single digits of each number, and then multiplying by place value.
The strategies explained in all sections of operational strategies are linked specifically with place value concepts and use expanded form repeatedly to build students' place value understanding in operations. This connection of operations and place value provides practice of algorithms while creating understanding of how the operations relate to place value and why place value understanding is crucial to deeper understanding of operations.

Comments: