Activities
The activities will match each strategy section above for use in the classroom.
Activity 1: Naming numbers and expanded form
Materials:
Playing cards 1-9, four of each card
Place value mat
Score sheet
Students will practice building two digit numbers, naming the place value name, writing the expanded form, and determining the number with the greatest value. This activity is in a form of a game. The object of the game is to form the largest value with two playing cards. First, students draw two cards each. The student will decide which number to place in the tens and ones place. The student is trying to create the largest number from the two cards drawn. The student then places the cards on the mat, either in the tens place or the ones place, and record the information for his or her cards on the score sheet. The partner does the same task and the two students determine who has the larger value. The student with the larger value takes all four cards and wins the round. This game practices the naming of numbers and expanded form but the act of making the largest value practices place value concepts of understanding the tens place has more value, regardless of digit, than the ones place.
Sample Round
Student A draws cards 4 and 7. To make the largest value she places the 7 in the tens place and 4 in the ones place making the number 74. Student B draws cards 1 and 8. Student B places card 8 in the tens place and card 1 in the ones place making the number 81. The score sheet shows:

The game can add variations depending on class need or student need. One variation could include three digit numbers. Another, the game could be played with multiple players, the player with the largest number taking all the cards played in the round. To add to strategy the players could each draw three cards and then chose which two to play and have one to discard. The score sheet could include a base ten picture representation. An assessment for the activity beyond the score sheet is to have the student explain why placing the higher value in the tens place makes a more valuable number. Another ideas is to have a response sheet giving a scenario and having the student respond, "Carla draws a 1 card and a 9 card, which place should each card go to win the round? Explain to her why this creates the highest value?" Another way is to pose a mistake scenario, "Carla draws a 1 card and a 9 card, she places the 1 in the tens place and the 9 in the ones place, she loses the round to her opponent, what advice would you give Carla to have a winning strategy?" Both questions ask the student to use place value concepts and understanding in the reply.
Activity 2: Addition of multidigit numbers
The addition of mulitdigit numbers is interesting when using relatable real world examples with students. Examples of attendance at professional sports games, heights of buildings or mountains, or distances on a map are examples of problems with meaningful context. For instance, my family is planning a trip from Chicago to Detroit and then Detroit to Cleveland. The distance to Detroit is 281 miles and the distance from Detroit to Cleveland is 169 miles. How many total miles will my family drive? The problems can be of any multidigit make-up and should have variety, some with and some without trade. The importance is not the values but the practice of expanding the form of each number and combining like terms. The table below shows the different expanded forms students can chose from the strategies. The student work should replicate the model shown for each step of the solution.
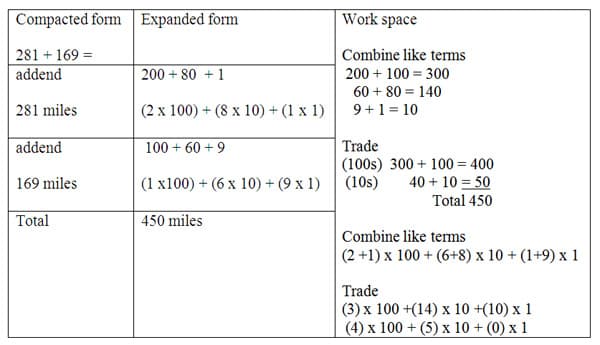
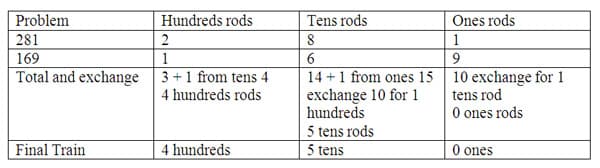
The students could also construct the addition problem with rods to make trains. The first train would have 2 hundreds rods, 8 tens rods and 1 ones rod. The second train added would have 1 hundreds rod, 6 tens rods and 9 ones rods. The reorganization of rods with like place values will have 3 hundreds rods, 14 ten rods and 10 ones rods. An exchange is needed in the ones place, exchange of 10 ones rod for 1 ten rods leaves 0 ones rods. Then exchange 10 of the 15 tens rods for 1 hundreds rod, leaving 5 tens rods, then counting the total 4 hundreds rods. The total train after exchange has 4 hundreds rods, 5 tens rods and 0 ones rods.
Activity 3: Subtraction of multidigit numbers
The use of real world examples and problems is excellent for subtraction problems. The link to real world in both addition and subtraction operations gives students practice at solving word problems and using examples of real math situations. An example question, The Willis Tower is Chicago is 442 m in height, the John Hancock Center in Chicago is 343 m in height. How much taller is the Willis Tower? The template for subtraction is similar to the addition template and allows for the same expanded number and combination of like terms.
Template
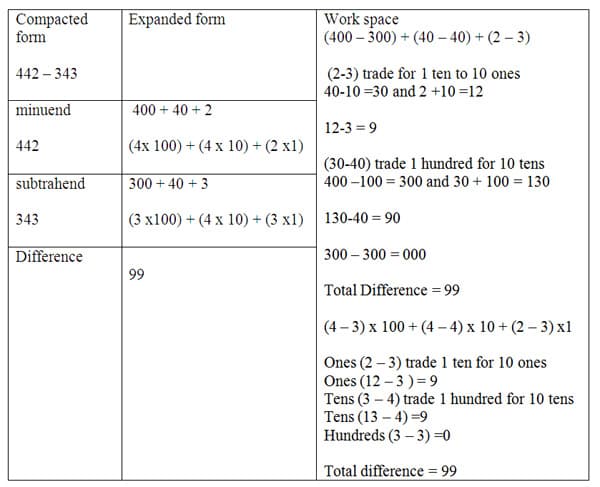
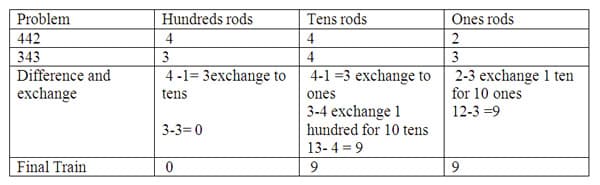
The train model can also be used to model the subtraction process. Make a minuend (total number and starting value) 442 train with 4 hundreds rods, 4 tens rods, and 2 ones rods. Next make a subtrahend (number subtracted) rod below the minuend with 343 train of 3 hundreds rods, 4 tens rods and 3 ones rods. The difference can be shown exchanging 1 tens rod for ten ones and then removing three from both trains, leaving 9 ones. The minuend now has 3 tens rods and 4 tens rods need to be subtracted so an exchange of 1 hundreds rod is needed. The hundreds rod exchanges for 10 tens making 13 tens subtract 4 tens leaving 9 tens. The hundreds rods are now equal at 3 which leaves 0 hundreds rods remaining.
Another way to solve is with the number line. On the number line find the Willis tower height of 442. Next, find the height of the John Hancock at 343. The student can count up to 343 to 350 and record 7 then skip count by 10s from 440 count 360 as 10 more, 370 as 20 more 380 as 30 more, 390 as 40 more 400 as 50 more until 440 is 90 more. At 440 counting to 442 is 2 more. The student can now combine all the counted up values of 7+90+2 for a total of 99 more.

Difference= 7+90 +2 = 99
Each word problem has a written model for the number model and then each step in the strategy can be shown in the workspace in each template. The written steps to solve are a way to track thinking for students and to express conceptual understanding. The step-by-step solving can be reduced to traditional methods once the student has strong conceptual understanding. The tedious process of unpacking each stage is time consuming in the beginning, but is meaningful and supports students' understanding of place value concepts.
Activity 3: Multiplication of multidigit numbers
The multidigit multiplication activity is fun for students to create their own problems from advertisements or sports pages of a newspaper. An example would be for a student to find an item for sale in a local advertisement. An electronics store may have computers on sale for $549. If the student wants to determine the cost for an entire classroom of 24 students to have a personal computer how much would all the computers cost? This problem provides real world examples and practices the skill of multiplication of multidigit numbers. The student could solve using the grid or by putting each with each by place value. For the grid the student could create a 3 x 2 grid and place the 500, 40 and 9 (from the expanded form of 549 as 500 + 40 + 9) along the top of the grid. Then place the 20 and 4 along the vertical side. Fill in each grid space with the product from the vertical and horizontal numbers on the grid. Add all the grid products to find the total. The other option is to solve with the "each with each" strategy of expanded both numbers and multiplying each factor place value by the second expanded number.
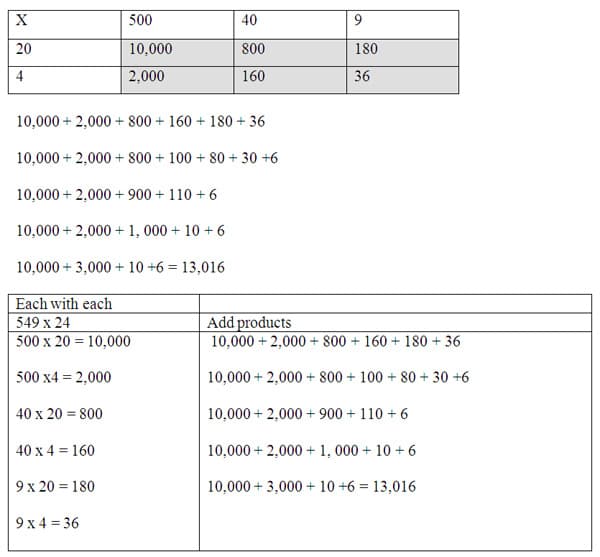
The students can find and create their own problems and then solve (as shown above) with each step in the process. Taking the steps to combine place values in the addition of the products reinforces the combination of like terms in place values and also the trading 10 to the next place value to exchange for one. In the problem above, 110 was broken into 100 +10 and then combined 1 hundred with the 900. Even as the most advanced problem in the activities the basic skills of exchanging and place value concepts are practice and reinforced in this type of problem.
An example of a sports problem could be a Chicago Bear running back ran for an average of 95 yards a game for 11 games. How many total yards did he run in the 11 games using his average yards per game? In this example, the student can use the same two strategies of the grid or the each with each strategy. If the grid is chosen the 90 and 5 can be placed horizontally and the 10 and 1 can be placed on the grid vertically. In the case of each with each 90 is multiplied by 10 and by 1 and the 5 is multiplied by the 10 and the 1, so each term is multiplied by the other factors terms.
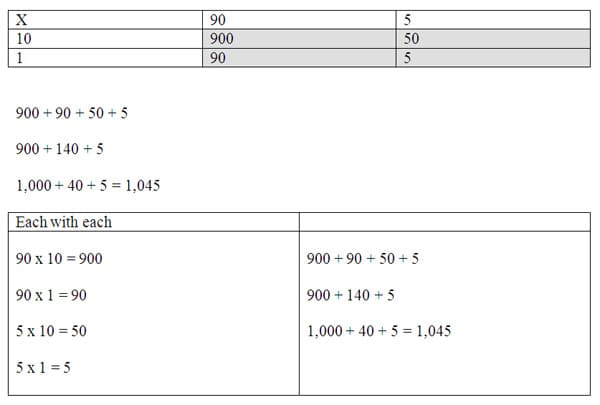
Each of these activities uses examples that students can find in real life and the problems make math operations meaningful. The strategies to solve have students unpack the problems into place value expanded form and practice combining like terms and trading. The combination and trading are at the root concepts of place value understanding. The step-by-step problem solving allows the students' to articulate each part of the process in the operation and can support students when explaining how and why a solution to a problem is found.
Materials List
Base ten blocks – Base ten block manipulatives traditionally have ones cubes, ten cubes as one tens rod and one hundred cubes together on a square flat representing hundreds. These concrete objects allow children to move and manipulate number models.
Digit cards – Digit cards are representative of the place value numbers in expanded form. The digit cards have each place value with 1-9 digits on each card. The thousands place digit cards have 1,000, 2,000, 3,000, 4,000, 5,000, 6,000, 7,000, 8,000, and 9,000. The number 4,562 can be shown by taken the digit cards 4,000 and 500 and 60 and 2.
Number lines – Number lines can be traditional measurement style number lines or can be created to show skip counting of numbers depending on a student's needs.
Rods – Rods are place value representatives similar to base ten blocks but are linear models. The one cube and ten rod are similar to the base ten blocks but a hundreds rod is a long rod that shows the length of one hundred.
Activity Sheets – The activity sheets below are paired with activities 1 and 2 from the section above.
Activity 1: Game sheet

Activity 1: Score sheet
Activity 2: Addition of Multidigit numbers
Template

Comments: