Background
Students that are being taught this unit should have a working knowledge of the rules of exponents. They should also be familiar with the concepts of variables, operations involving integers and combining like terms involving variables. Students will be working with a significant amount of mathematical notation and they should know the order of operations as well as proper mathematical notation. This will help students to be able to complete some of the problems they will be presented.
Zero and Place Value
Our number system is called the decimal system and it is based on the number ten. The word decimal is derived from the Latin word decim. 1 There is no clear history of how we arrived at our current number system but the rough outline, and some specifics are known. A key feature in the overall scheme is the number zero and its value as a placeholder.
The number zero is important because of its use as a place value. Think about the difference of 1,001 dollars versus 11 dollars. The number zero is used to provide an unambiguous way of reading numbers. How else would we know that there are one thousand dollars in addition to the one dollar? We can write the number without the use of words thanks to zeros which hold the place value for us.
The ancient Babylonians had a base sixty number system. They had a separate representation for all the numbers up to sixty. 2 This is one of the main reasons our hour has sixty minutes and sixty seconds make up one minute. In our current system we have separate representations for all numbers up to ten. The ancient Mayans had a base twenty number system in which a dot represented the number one and a horizontal line represented the number five. The Spanish explorers discovered this system and the significance of this was that their concept of zero as a placeholder was very similar to ours as we write numbers today. The numbers one through twenty in Mayan would look like this:
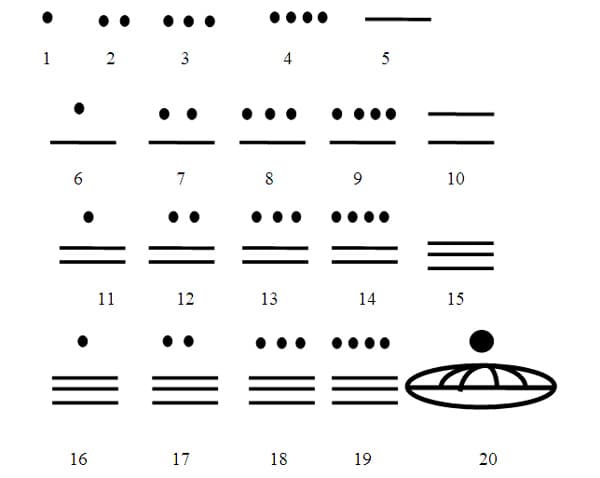
Notice the one representation and then the special symbol which represented zero. The Mayan twenty would be equivalent to our number ten. The use of symbol representation used as a place holder was common among many cultures and the base number system that they used varied widely. 3 By the eighth century in India, our modern decimal system with zero as a place holder was developed. 4
I will work to make sure that my students really understand the key role that zero plays as a place holder. The digits 0,1,2,3,4,5,6,7,8,9 are the basis for our entire number system. The number ten (10) is written with two digits with the 1 standing for 1 ten, and the zero indicating zero 1s. We know that the 1 represents a ten and not a one or a hundred, because of the single zero to its right. As simple as this idea is, it gives the decimal system tremendous power for representing even very large (relative to everyday experience) numbers compactly.

Comments: