Liping Ma
Introduction and Rationale
The way we teach the concept of fractions in much of the United States has been inadequate for too long. I have watched teachers representing the same fractions with the same pie diagrams for the past 20 years. Students have little concept of fractional values, struggle with algorithms involving fractions, find it difficult to prove equivalence and will generally do anything possible to avoid having to use fractions. I would like to address some of the mistakes I and other teachers have made in the past.
For years, I have asked students to order fractions and decimals on a number line. I've asked them this for multiple reasons: First, to assist in the understanding and practice of determining order and relative size of rational numbers. Second, to recognize that without being able to find common denominators for fractions, and an understanding of place value for decimals, it is very difficult to determine where some numbers should be placed on a number line. Third, to examine the distances between numbers on a line as a means for comparing values. In other words, the distance from 1/2 to 3/4 should not only be greater than the distance from 1/2 to 2/3, but have a proportional relationship so that the measurement of these distances can be used to place other fractions correctly on this length line. Theses three reasons have helped frame two of my objectives and goals for this unit. I believe the measurement and precision component of this unit will address many misconceptions regarding fractional value and offer an alternative way to look at operations (such as addition, subtraction, multiplication and division) with rational numbers.
If I give students a series of fractions to place on a number line, many of them will have the order absolutely correct. They will know through experience or use of common denominator calculations, factors and multiples of the numbers being worked with, that 1/2 is less than 3/4 and that 2/3 falls on a line somewhere between the first 2. Some may even divide the denominators into the numerators and get a decimal so they may use the strategies of "place value" to determine order. What most of the students are not able to do is place the fractions on a line with precision. A simplest example illustrating this is that students often do not depict the distance from 0 to 1/2 as the same as the distance from 1/2 to 1. Showing a measureable equality between the two distances may be achieved by some students, but I believe often only through sheer luck. I recently gave students in my 7 th grade Pre-Algebra courses a series of fractions and decimals to order on a number line of their own creation. I observed their process carefully and saw that students failed to use any tools to assist in the placement of non-"benchmark" fractions (i.e. fractions other than the familiar 1/2, 1/4, etc.). A few kids folded their paper in half to start the fraction/ decimal placements, but no student went beyond that. In fact, graph paper was made available to students and half of them chose not to use it. After reviewing their work it was apparent that the spacing/intervals were random.
The motivations for writing this unit came from a few different experiences I've had over the past couple years. In addition to what I've described above, I have witnessed year after year, students mistaking the measurement of an array by counting the lines instead of counting the space. This is significant because 2 dimensional geometry is actually taught as measurement, (a focus which number lines have not typically been afforded). The array in figure a. is a typical example of a 6 th and 7 th grade beginning geometry problem. Students will solve for perimeter in one of two ways: Some will
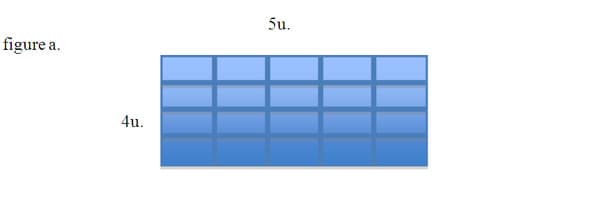
say that the length of the shape is 5 units and the width is 4 units. This gives us a perimeter of 18 units and an area of 20 square units. Others will argue that this is a 6 unit by 5 unit rectangle, giving us a perimeter of 22 units and an area of 30 square units.
On an even more basic level, given a number line (figure b.) of 7 units, fully 50% - 60% of 5 th and 6 th graders quizzed would claim the line to be 8 units long. It seems that whether we were working on a geometry unit or a simple number line , there was a significant percent of students not recognizing that units represent space instead of marks.

I teach in the Brisbane Elementary School District at Lipman Middle School. Over the past 3 years I have taught 6 th grade mathematics, 7 th grade pre-algebra and 8 th grade algebra. This was a difficult assignment over a three year period, not having a consistent curriculum to draw on and build upon made for busy curriculum design years. A benefit to this series of assignments was having the ability to see a middle school child's academic progression. The most positively striking progression I have noticed is their ability to understand and work in abstract concepts. The area of mathematics that seems to show the least amount of progression comes in the form of fractions. Whether it be determining value, simplifying, adding, subtracting, multiplying or dividing, most if not all students come with at best a lack of confidence and at worst a serious fear.
A lack of confidence when working with fractions combined with a lack of understanding that fractions have value is the basic premise I am working from in this unit. I believe that students will gain a clearer understanding of rational numbers, fractions in particular, when the concept is presented with context. Using a number line should go a long way in solidifying this understanding, so that the higher level mathematics our students are struggling will become easier.
In 1989 the National Council for the Teaching of Mathematics (NCTM) asserted that American students were woefully prepared for the rigors of secondary mathematics. Much of this stemmed from their superficial and algorithm based understanding of Proportional Reasoning. The study noted, "proportional reasoning is of such great importance that it merits whatever time and effort must be expended to assure its careful development." 1Students were taught methods such as cross products to solve for missing values in a set of ratios. They were not taught why they were doing this, nor it's applications beyond this one type of problem. In Liping Ma's book, Knowing and Teaching Mathematics, a teacher from China she was interviewing stated, "it is not enough to know how, we must know why". These words have been lost on many teachers of mathematics, many textbook companies, universitiies and of course on politicians, who in "pushing down" standards to lower grades in order to compete have effectively forced classrooms to teach on the surface of concepts instead of digging deeply into them.

Comments: