Major Objective Background
Fractions
For the sake of this unit, the fraction background will be limited to: Unit fractions, general fractions, the equivalence of fractions, adding and subtracting fractions with like and unlike denominators and multiplication of fractions.
Unit Fraction
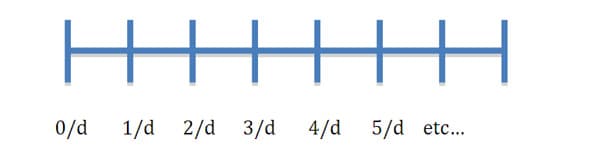
A unit fraction is a fraction of the form 1/d (for any positive integer d). The concept of the unit fraction 1/d may be the most important foundational step in the study of fractions. Students need to understand that 1/d represents one of d equal parts, with emphasis placed on the word equal. 1 of d equal parts can be illustrated on the number line by dividing the interval between 0 and 1 into d equal parts. The first segment represents the unit fraction 1/d, while the first two parts together represent 2/d parts. Each of the two parts being equal. The first 3 parts represent 3/d, (three of d equal parts) and so on. Susan Lamon acknowledges in her book, Teaching Fractions and Ratios for Understanding, that the ancient Egyptians used unit fractions extensively. These fractions whose numerators are all 1 are easy to compare. She points out that any unit fraction can be written as the sum of other unit fractions.
General Fractions
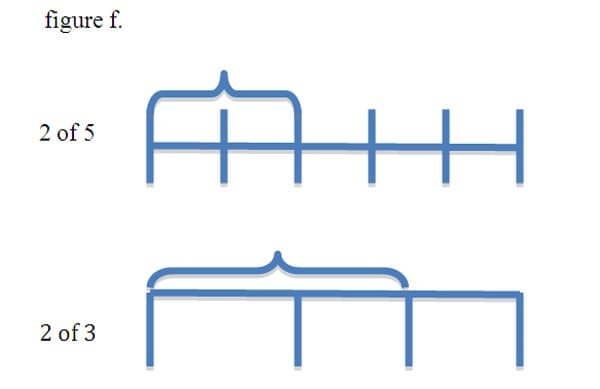
A general fraction is a non-negative rational number symbolically represented as n/d. Here, d is the number of equal parts of necessary to make a whole, and n is the number of copies of these equal parts. In other words, n copies of the unit fraction 1/d or (n)*1/d=n/d. The top number of a fraction is called the numerator and the bottom number is called the denominator. The denominator tells us the size of the pieces. The larger the denominator the smaller the size of each part since the whole is divided up into more parts. For example, 2/3 and 2/5 have the same number of parts, but2/5 has smaller pieces, (figure f.).
According to Lamon, "The order of the numbers is important. Thus, fractions are ordered pairs of numbers: 3/4 is not the same as the fracion 4/3" 4
Equivalence
"The Theorem of Equivalence may be regarded as the fundamental fact in the subject of fractions. Conceptually, its message is clear: the essence of the fraction symbol m/n lies not so much in the individual numbers m and n of the symbol but in their 'relative size' because m/n = 2m/2n=3m/3n ," 5 says Wu. This theorem helps us understand something we believe to be second nature to our children, that is, the idea that 1/2=2/4 is translatable to all equivalent fractions. Problems with this assumption arise when students are asked to compare fractions like 8/12 and 18/27. The relationship between these two equivalent fractions is not as easy to see as with 1/2=2/4, one which is a simple integer multiple of the other. Instead, the equivalence between 8/12 and 18/27 is most easily seen after reducing each to their simplified form of 2/3.
Addition and Subtraction of Fractions with Like Denominators
Our students have most likely already learned to add and subtract like and related fractions. Just in case these concepts are unfamiliar here is a quick review. Like fractions are fractions with the same denominator. Addition and subtraction problems involving like fractions involve only addition and subtraction of the fractions' numerators. Symbolically this would be represented as a/b+c/b=(a+c)/b. The denominators of these fractions are not summed because they represent the "whole".
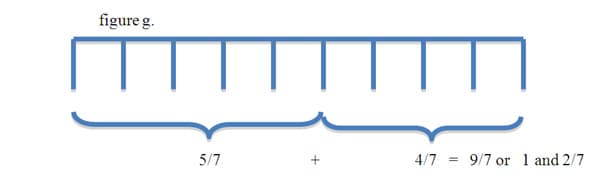
In some cases the sum of the numerators added will exceed the denominator value. This is when we begin dealing with improper fractions or mixed numbers. The addition problem 5/7+4/7=9/7, for example, is easily depicted using the number line. In this problem we have two fractions with the same denominators (7), so we will need only2/7 added to 5/7to complete the whole. We have 2/7 more than that giving us 9/7. Another way of reading this is, 7/7 makes one whole with 2/7 left over, giving us the mixed number of 1(2/7). An improper fraction is defined as a general fraction n/d where the number of parts (n) is greater than the whole (d). A mixed number represents the quotient of that improper fraction, thus 9 divided by 7 gives us 1 and 2/7.
Addition and Subtraction of Related Fractions
Primary mathematics standards describe related fractions as follows: "Related fractions are fractions where the where the denominator of one fraction is a simple multiple of the denominator of the other fraction." 6 Addition and subtraction problems involving related fractions require finding an equivalent fraction for only one of the set of two you are working with. The rules of equivalence will help the students at this juncture. To illustrate this concept, consider the addition problem 2/3+4/9. We can see that 3 is a factor of 9 so the only fraction that needs to be changed would be 2/3. If we multiply this fraction by 1, represented as 3/3, our new problem becomes: 6/9+4/9. Now we can sum these fractions as in the case of like fractions discussed above.
Addition and Subtraction of Fractions with Unlike Denominators
Adding and subtracting fractions with unlike denominators where the denominators are not simple multiples of each other is the step our students seem have most trouble with. If this is taken in a step by step process, where different grade levels have different responsibilities, I believe we would have much more success. The first step in dealing with unlike denominators would be to multiply the numerator and denominator of each fraction by the denominator of the other to obtain equivalent fractions that share the same denominator with each other. For example:
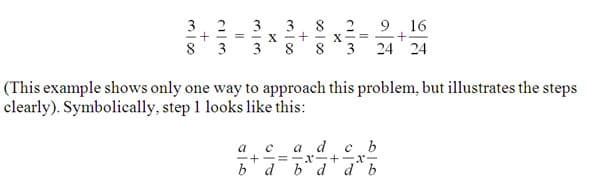
The second step would be to work with students to find the lowest common denominator of two unrelated fractions, alternatively called, the lowest common multiple, (lcm). This is a necessary step for students so they can work towards less simplifying after solving. Students should begin this step by learning to compare simple general fractions through experimentation with bars and number lines. Adding fractions like 2/3 and 3/4 will break down with bars and number lines in the same way. See figure
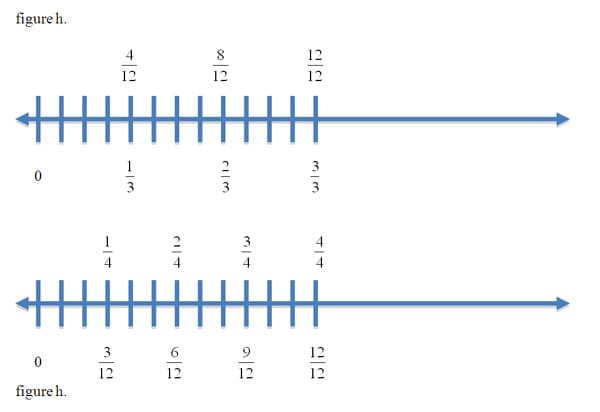
If students place iterations of each relevant unit fraction on a line, i.e. 1/3,2/3,3/3 and 1/4,2/4,3/4 and 4/4 then subdivide these lines into an equal number of total parts (d) or 12 for the sake of this example, they will be able to add, subtract and compare all iterations of the original fractions because these two general fractions now share a common "whole" or a common denominator. The denominator of 12 is found by recognizing the lowest common multiple (lcm) of 3 and 4 is 12.
I believe this next step in the process underscores my appendix advocating for revisiting common algorithms in higher grades. If we continue to open our students up to new ways of looking at basic concepts we will only strengthen their foundations.
Multiplication of Unit Fractions and General Fractions by Whole Numbers
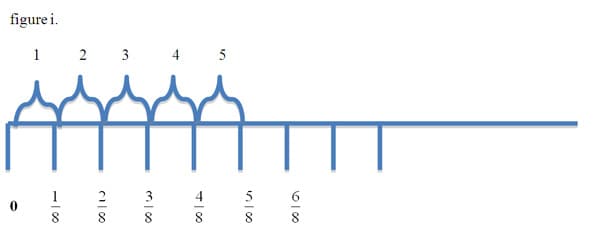
The initial multiplication operations fit neatly on the number line format. Multiplying a unit fraction by a whole number can be thought of as repeated addition of that unit fraction. A problem such as, (1/8) x 5, can be thought of as 5 iterations of the unit fraction 1/8. (figure i.).
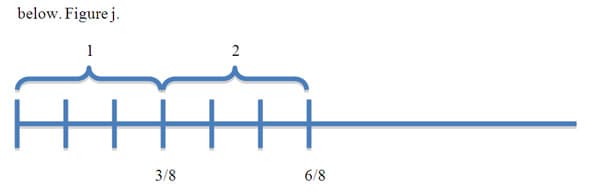
Multiplying general fractions by whole numbers such as, (3/8) x 2, will operate in the same way as iterating unit fractions. The difference being, we iterate every third unit (based on a 3/8 example), giving us a total of 6/8. This is illustrated with the number line
below. Figure j.
Multiplying Fractions by Fractions
Multiplying a fraction by another fraction may be best accomplished with a grid (array). It is also possible to multiply fractions by using the number line. I believe it is important conceptually to help students understand that the product obtained after multiplying two fractions will be smaller than either of the two original fractions. This situation is opposite from that of multiplication of two whole numbers: 15 = 5 x 3 is larger than both 5 and 3, while 1/15 = 1/5 x 1/3 is smaller than both 1/5 and 1/3. Using related unit fractions (whose denominators are factors of each other and whose numerators are 1) will be a nice entry into the concept. To illustrate1/2 x 1/4, for example, students could begin by finding the product of the relevant unit fractions 1/2 and 1/4 by subdividing a unit interval into fourths and then finding 1/2 of one fourth to obtain the product of 1/8. To find the original product of 1/2 x 3/4, students could proceed by continuing to subdivide each of the four fourths in half, and then iterating 3 copies of the 1/8 just found. The example below illustrates this concept.
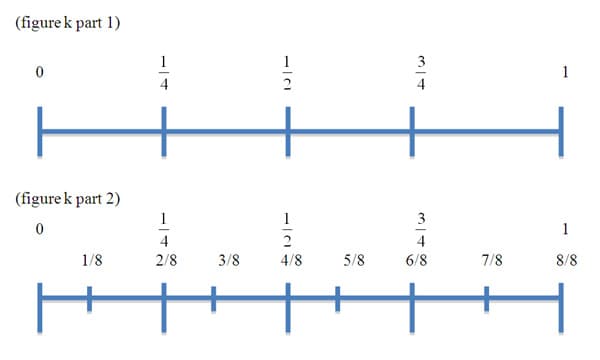
It is important for students to have a concrete understanding of the product of a fraction before simply multiplying numerators and denominators. I believe having the students measure and plot these simple related fraction problems on a number line will go a long way towards the concrete understanding we are looking for.

Comments: