Foundational Goals Background
Number Lines
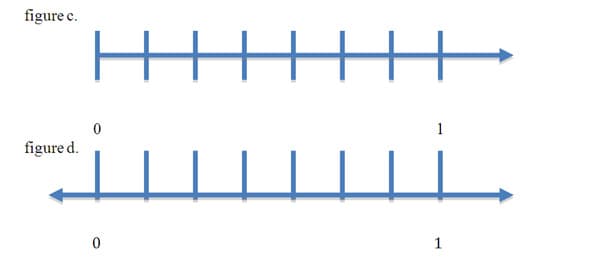
Number lines and rays are typically represented as horizontal lines. Positive numbers are equally spaced to the right of the zero and negative numbers equally spaced to the left. This concept of equality with regard to the iterations on a number line is clearly shown when placing whole numbers on a line. An equal measureable distance between each whole number will continue infinitely. A number ray is determined by a fixed point, (0 in figure c.) and continuing on infinitely in this one direction. A number line is determined by two points, a "zero" point and a "one" as shown in figure d and continues in both directions infinitely. For the sake of this unit our number lines and rays will only work in a positive direction or to the right of the "zero".
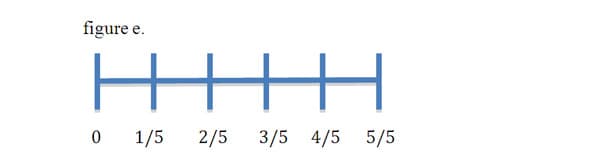
According to H. Wu of U.C. Berkeley,"as a model for fractions, the number line differs from other models in several important ways, first a length represents the unit, and the number line model suggests not only iteration of the unit, but also simultaneous subdivisions of all iterated units. That is, the number line can be treated as a ruler." 2 Each of these iterated units, when representing fractions will be 1/d, where d represents the number of units necessary to make a whole unit. In other words, when subdividing a line into ?, it will take 5 iterations to complete the whole (figure e.). These fraction concepts are explained in greater detail in the fractions section of my background.
Early number lines were most likely measurements also. Ancient Egyptians did not have a concept of zero, but are believed to have used lines with consistent intervals in order to gauge distance while building. The number line was founded with the idea of measurement, not counting. According to reports from the International Study Group on Ethnomathematics, "archeologists reference, 'leveling lines' that predate the pyramids. Lines that measure foundation depth and height using the ground as the zero level, or as the Egyptologist, George Reisner calls it, "Zero Lines". These zero lines were labeled nfr, or zero." 3 Level lines were evenly spaced above and below the nfr and labeled, 1 cubit above nfr, 2 cubits above nfr or 1 cubit below nfr, 2 cubits below nfr. Number lines have historically been tools for measurement. In this unit we will attempt to get back to this idea.
The basic operations of addition, subtraction and multiplication as well as measurement and division will be addressed in the strategy section for Foundational Goals.

Comments: