Mathematics Background
In researching the development of understanding expressions in the CCSS-M, I have sectioned the progression into six big ideas with the skills needed to grasp each of those big ideas: writing numerical expressions; representing unknown quantities using variables; representing word problems as expressions; evaluating expressions for given values; transforming expressions, motivated by number tricks; and equivalent expressions,. I have included descriptions, too, of the types of activities that will be used to elicit these skills and ideas while building on the prior knowledge students bring to class. Many of the topics overlap, but the subtle shifts along the progression are essential for students to understand, which is why the divisions are made as they are.
Throughout these chunks of the units, challenging word problems will be woven so that students develop an understanding of the relationships between the contexts of problems and their expressions. The results of a teacher-researcher study revealed what are often considered algebraic problems may lack algebraic thinking. They stated, "...implementation can impact how algebraic a lesson really is. For example, the lesson could have easily turned into a problem of 'adding on by twos' when students completed a function table, potentially rendering the lesson an arithmetic task instead of an algebraic one" (Ernest and Balti, 2008). As a result of the study, three instructional strategies that "helped keep the algebra in the foreground of the lesson" were identified.
The first strategy Ernest and Balti established is using unexecuted expressions. By leaving a sequence uncomputed, (for example, 3 x 2 + 2), students are able to connect each term and operation of the expression to its original context. This encourages sense-making about the problem, which leads to a grasp of why the expression works after generalizing it. Often, students are adept at "answer-getting" but have little understanding of what their numerical results represent or why they make sense in the context of the problem. While they initially formulate rules to represent situations, it is helpful to practice using unexecuted expressions to gain insight into students' reasoning and to address any misconceptions they have before simplifying them.
The second strategy is using large numbers. When students investigate a relationship, they often solve for new inputs using the previous inputs. For example, if they see consecutive outputs of 5, 8, 11, and 14 for the inputs 0-4, they may state the rule as "add 3 each time the input increases by 1." While this is a true statement, it requires recursivity, or knowing the previous term to find the next. By asking students to determine the output when the input is 100, or 1000, or any arbitrary large number, they are forced to realize the inefficiency of using their current rule to determine it. This shift in seeing the "horizontal" relationship between variables in a table is often difficult for students, but posing a problem that makes it the only feasible way to solve gives them a purpose for using it.
All of the work outlined in the previous two paragraphs still does not guarantee algebraic thinking and reasoning, especially in the absence of using representational context. Often, students are able to generate expressions without making clear connections to the contexts to which they relate. Again, this shift away from being satisfied with answer-getting makes the learning important beyond the given task; students need to be able to make connections across various representations in order to develop strategic thinking that will enable them to attack diverse problems effectively. This can be promoted through presenting a variety of contexts for problems, including visual representations, and consistently asking what each term in an expression stands for. This will be discussed further in the section on variables, where students' misconceptions become very evident if they are not in the habit of explicitly defining units in their calculations and solutions.
Writing Numerical Expressions
Students have been writing numerical expressions throughout their careers working with operations, such as
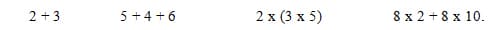
They bring important prior knowledge to the table in the form of experience working with the properties of operations informally in the context of operations of whole numbers. Most of the experiences they have had with expressions have been limited to whole numbers, and while occasional fractions and variables have been included in isolated problems, the understanding of an expression as showing a relationship between or among quantities is not yet evident. In order to give meaning to expressions, students must become more flexible in their definitions of them and formalize their understanding of the basic properties for arithmetic, especially the Commutative, Associative, Identity, Inverse Rules for Addition and for Multiplication, and the Distributive Rule. This will be accomplished through diverse experiences with problem sets delivered through Number Talk strings over several days that require them to build on what they know to incorporate numbers in different forms and a wide selection of expressions.
Students will start to see what powerful tools expressions are, especially in that they can be used flexibly to accomplish specific purposes students will need to address in solving problems. In essence, expressions are "recipes" for computations that will become increasingly complex as students progress through algebra. Reaching this realization will require them to see expressions as objects in their own right and to connect their meaning to the contexts in which they are developed. By building solid understanding of numerical expressions, they will be better able to transition into using variables with meaning in expressions and eventually apply this knowledge to equations.
Representing Unknown Quantities using Variables
The introduction of variables is typically done without fanfare; it is simply presented as replacing numbers with letters. However, this provides little sense of their importance and utility. Variables need to be understood as standing for any quantity within an expression, whose meaning is determined by the surrounding context. It is the meaning that is often lost when students begin using variables. Interviews with students revealed that "the ability to verbally describe a method does not necessarily entail the ability to symbolize that method mathematically," (Nesher and Kilpatrick, 1990). This suggests that there are stages in the development of understanding notation.
So how do students approach problems in algebra? "Many of the cognitive studies in the learning and teaching of algebra have focused on students' approaches to equation solving. These approaches have been classified into three types: intuitive, trial-and-error substitution, and formal," (Nesher and Kilpatrick, 1990). Often, especially in algebra, we rush into formal approaches by teaching students established algorithms without connecting to or building on their intuitive approaches. I believe that this is especially detrimental when introducing variables because it assumes too much prior understanding by the student and, if left unaddressed, can lead to a weak foundation that will eventually crumble.
Since working with expressions is a crucial step toward proficiency with equations, it is important to meet students where they are, honoring their prior knowledge and intuition, and building toward formalization. To do this, students need many experiences with problems that logically progress toward a point where their intuitive and trial-and-error methods (my students refer to this as "guess-and-check") are no longer effective or efficient. Eventually, they will see the need for variables, too, to express generalizations in a formal language. A sample problem set might progress like this:
- Each group of desks in our classroom seats four students. How many students will fit in 2 groups? 4 groups? 7 groups? How did you find that?
- Each row in the movie theater seats 12 people. How many rows would a group of 24 people need? 48 people? 156 people? How did you find that?
- Mr. Jimenez rented square tables (only one person could fit at each side of the table) for the 8th grade luncheon. He pushed the tables together to form one long row. How many guests could be seated with a row of 10 tables? 20 tables? How did you solve? Can you find a rule to tell how many people could be seated in a row of n tables? Explain how your rule relates to the situation.
When students calculate the solutions to each set of problems, the questions repeatedly ask, "Why do you think that?" or "How did you figure that out?" This mantra will make the transition into writing expressions easier for students to see. When different inputs are given, asking what they are doing each time develops structure. Then the question becomes, "Can we represent that relationship somehow so that it works with any number?" Students may naturally insert a variable, depending on their previous exposure, or they may verbalize that there is a step at which any number can be inserted into the operation. Either way, their variables now have meaning and students are ready to evaluate expressions knowing what their answers mean.
Beyond understanding how variables work, students will need to consistently label their work with units to connect the computations to the contexts of problems. This will build from our prior work with fractions and will serve as a focal point of discussion. I have come to believe that understanding units is key to students making sense of the problems they encounter; it is another often overlooked part of problem solving that seems obvious to us as experienced mathematicians, but can create gaps in understanding and reasoning for our students who are new to working with unknowns in these contexts.
Evaluating Expressions for Given Values
The purpose of doing all the work needed to construct expressions to represent situations is to make our lives easier when we need to solve for a variety of inputs that range in value from very small to very large numbers. Still working from word problems, students will construct expressions to solve and then will practice evaluating for given values. I will integrate negative and fraction inputs to increase their comfort and capacity dealing with non-whole numbers.
This point in the unit leads to more formalization of the thinking students have been using, so I will model organizing their inputs and outputs into tables to help forge the path into equations and graphing functions that will come later in the year. Students will see the power of having generalized expressions to use in solving problems by the ease in which they are able to find outputs. They will begin to notice patterns in tables and make conjectures about extending single expressions into equations that state two or more expressions are equal.
Number Tricks: Formalizing Notation to Transform and Simplify Expressions
Putting a positive spin on the mystery of mathematics is something that number tricks can accomplish in helping students navigate the road to formal notation which will enable them to transform expressions. Number tricks are series of instructions given to students that lead to some predictable answer. For example, if students choose a number, add 5, subtract 2, multiply by 3 and then subtract 3, they will end up with 3 times their starting number plus 6. I will play the game with students having worked out the simplified form of the expression so that they can give me any input and I will be able to quickly tell them their output. I can also ask them for the output and add four to get their input. ??
After working with some examples of number tricks where there is a simple rule like x + 1to get from the starting number to the ending number, I will expose students to some where the variable cancels and there is a constant answer. This type of number trick will lead us nicely into simplifying expressions and the effects of applying the basic rules of arithmetic to a series of steps.
Repeated rounds of number tricks will be played with students to pique their interest and then the mystery will be revealed. We will represent each step in symbolic form, building upon the previous steps. Finally, we will apply the properties of arithmetic to simplify the expressions as far as they can be to reveal the trick of how I was able to "guess" their numbers so quickly. We will formalize the process of simplifying through other examples, and students will craft their own number tricks to represent in words and symbolically to practice these skills.
Equivalent Expressions
Now that students have gathered many tools for working with expressions, they will apply them to compare expressions and test for equivalence. Since students are now comfortable with the fact that numbers can be represented in various forms, they will formalize some of the conventions that allow this to occur. We will explore two methods for determining equivalence, both of which apply concepts students have been exploring in this unit.
One way to test for equivalence in one-variable expressions is to evaluate the expressions for the same input value. If the resulting output is always the same, for any input, the expressions are equivalent. (In fact, for the expressions we will construct, which will all be linear in the variable, it will be enough to check for 2 values; but I will ignore this point in class, because later they will probably encounter more complex expressions for which many comparisons may be needed.) An example of this would be comparing 2(x + 6) and 2x + 12. If I evaluate each for x = 2, I will get an output of 16. Connecting this to number tricks, I could give the recipe of "Choose a number, add six, then multiply the sum by 2," or, "Choose a number, multiply it by 2, then add 12 to the product," and I would get the same result if my chosen number was 2. Students will practice this skill given various expressions with whole numbers, fractions, and exponents.
The other method to test for equivalence is simplifying to check for representations of the expressions in the same form. Using the example above of 2(x + 6) and 2x + 12, students can apply the Distributive property to the first expression to make it represented in the same form as the second, proving they are equivalent. This will be a point to introduce the idea of using the Distributive Rule to combine like terms so that when they see expressions like 2x + 4 - 5x + 6 and -3x + 10, they will be able to simplify to show that they always yield the same result. This concept of equivalence will lead into our next unit where we will explore equations and the basic moves for solving.
Representing Word Problems as Algebraic Expressions
While students encounter word problems throughout the progression of the unit, it is a topic that deserves special attention, as it is frequently feared and avoided. At this point in their learning, students are ready to start generalizing the patterns they have been noting in how expressions are formed and what they mean. At this point, I will introduce a famous problem, "Diophantus's Age," which poses a math problem in verse:
His childhood lasted one sixth of his life; he grew a beard after one twelfth more; one seventh later, he was married. Five years later, he had a son. The son lived exactly half as long as his father. Four years later, Diophantus died. How old was he?
Initially daunting, this problem can be presented in a way that caters to students love affair with "guess and check" and extends it to a method of "Guess-Check-Generalize" (Cuoco, 2008). To solve this problem, students make a guess at Diophantus's age when he died. Sometimes interesting discussion will arise about lower life expectancies in earlier times, but most students guess somewhere between 60-100 years.
Next, students apply the verses to their guesses. As they come to solutions, they adjust their guesses up or down based on their results. They will follow this process with a total of 3 guesses until we can generalize. I will have three different students share their guesses and processes, writing the guesses in a different color than the rest of the steps. Students will see repetition in what we're doing, and we will replace the guesses with variables to generalize the expression and solve as an equation.
Ending this unit with this problem will lead us into working with equations. The transition at this point will provide an empowering view for students to take, as they will feel accomplished in solving what had appeared to be a difficult problem using a method that is transferable to any word problem requiring an equation to solve. It will also set the stage for our culminating unit project where they will apply their knowledge about expressions to represent an issue they care about mathematically.
Culminating Project
Recently, Chicago Magazine published a two-part story about the gross misrepresentation of crime statistics in Chicago. The details are horrifying and treat human life as a disposable commodity, so the graphic content is not appropriate for my sensitive young learners. However, it launched an urgency in me to share the power of its approach: investigating numbers that people in power would like us to simply accept and believe to be true representations of what is going on.
Helping students see the relevance of mathematics, particularly algebra, to their lives is one of the most difficult parts of my job. Students often tell me that no one in their families understands it either, so why should they have to? This is an important question. I understand that the skills developed through algebraic thinking make students more versatile and critical consumers of information, but the reality is that their experiences have not required them to apply these skills in the situations where problems typically apply them, such as buying cars or comparing cost of t-shirt companies.
Contrary to their beliefs, students do use this thinking in their daily lives for things they care deeply about such as computer and video games, music and other media, calculating their grades, and navigating the selective enrollment process for high school. This project aims to help them see the advantages mathematical thinking can provide in those contexts, as well as in helping them counteract injustices they face as a result of their race, English proficiency level, and socioeconomic status.
The project will develop over the course of this unit, beginning with weekly lessons during our Response to Intervention block that connect the issues around making informed decisions when choosing family phone plans, pricing pizza, understanding where the money goes when buying scalped concert tickets, and deciding whether or not to get a warranty on electronics. By engaging in analysis of these situations together, students will develop an understanding of how to apply mathematics to answer questions they have about situations they encounter. Throughout this time, they will generate lists of questions they have about issues and situations they care about, as well as gathering articles that speak to them in periodicals as starting points.
At the end of the unit, students will share their ideas in small groups and with the whole class to narrow their focuses. Students will use a graphic organizer to help focus their research to determine what they need to know, how they will find out, and how they will know when they have answered their question. They will have time in class to research, meet with me, and develop arguments that are mathematically sound to address the issues they choose. Communicating their findings will take place via posters, multimedia presentations, or videos that they will create and share at our first quarter report card pick up with their families who attend. A secondary but equally important goal of the culminating project is to set the tone for a year of mathematics learning with positive support and interest from the homes of my newly empowered students.

Comments: