From Arithmetic to Algebra: Variables, Word Problems, Fractions and the Rules

Math Background

Translating Verbal Statements to Find Equivalent Expressions

This unit will begin with translating verbal phrases into algebraic expressions, meaning students will be creating expressions from a series of words by distinguishing operations and how they should be set up. Before beginning to translate verbal statements into equivalent expressions, students will have learned the language necessary to convert, for example “twice a number plus seven” into an algebraic expression, as well as understand that algebraic expressions are directions to be able to compute. Students will be able to recognize that “twice a number” means 2 times some number that students can choose. This will be represented by some variable, a letter that represents the unknown number, and “plus seven” means that you are adding 7 to that term. Since both terms are in the form of one conjoined statement, they will know that they have to include both terms to create one linear expression in the form “ax + b”, where a and b are any numbers. In this case, the expression would be 2x + 7. Since they will also understand that 2x + 7 can be read as picking a number x multiplying it by 2 and adding 7, when finding expressions that are equivalent, if when they compute the expressions for any choice of number for x, they produce the same result, then they are indeed equivalent. For algebraic expressions to be equivalent, students should be able to choose any value for the variable x, substitute this value in the two expressions, compute the resulting numerical value, and they will always get the same answer. This unit will cover the more complex algebraic expressions that will require the use of multiple operations at one time. For example, I would like my students to be able to simplify an expression like 3((2x+7) – (4x – 5)) + 6(x – 5). It will be important to give clear instructions on translating the simple numerical and algebraic word phrases before moving on because then they will struggle with the more complex expressions being represented in this unit. Although students will have been introduced to the terminology involved in this topic, it will still be necessary to touch upon the vocabulary as a reminder. Some of this vocabulary includes expression, algebraic expression, equivalent, coefficient, constant, and variable.

In order to ensure that students understand the concept, it is necessary to scaffold. There are many types of complex word phrases, but they will be categorized into three groups, Tier 1, Tier 2, and Tier 3, to show growth in complexity. An example from each group would be,

Notice that each tier has multiple steps, but as the students go from one to the next, the questions will gradually become harder. This will allow them to work their way up to more complicated expressions. The question that will accompany this table, or each question separately, is “Determine which expressions are equivalent to the verbal statements. State which expression most closely represents the verbal phrase.” In the Tier 1 problem, students are given the variable that they should use in the expression in order for them to understand that it should be representing the number of counties in Wisconsin. It is necessary for students to understand the idea behind “less than” so that they know they are taking 4 away from the term 6c, which is representing “6 times the number of counties in Wisconsin,” to get the full expression 6c-4, answer choice b). Since the question also asks to determine which expressions are equivalent, there is another answer choice that will answer this question and that is answer choice c). Students may not know how to use the distributive rule just yet, but they will have been introduced to substitution earlier in the year. This will allow them to be able to substitute the variable c with any number to find which expressions are equivalent. For example, if c = 3, in answer choice b) students would get 6(3)-4=18-4=14. With this information and their knowledge on the meaning of equivalent expressions, students will be able to find the answer choice that is also equal to 14 in order to choose the correct equivalent expression. The answer choices were specifically created in order to catch any misconceptions that students might have while translating word phrases. The first answer choice touches on the mistake that students make when they see the phrase “less than.” They know it means to subtract, but they have a hard time realizing that it actually means that something is 4 units smaller than the original. The last answer choice addresses the misconception of conjoining terms that cannot be subtracted from one another.

Once students have chosen their equivalent expressions, a follow up question can be asked. An example of a follow up question is, “If Wisconsin has 72 counties and Oklahoma has 77 counties, is this correct? Show your work to justify your answer.” This touches on the process of substitution to check their work. Since they know that Wisconsin has 72 counties and in the expression c represents the number of counties in Wisconsin, they can substitute the 72 for the c to show Oklahoma would have 6(72)-4=432-4=428 counties, which is not true. To challenge students and allow them to formulate a variety of answers within the class, I will also ask them to formulate an expression that would give the correct answer. Students would have to define a variable for the number of counties that Wisconsin has and begin manipulating numbers and operations to create an expression that would equal 77, for example let c represent the number of counties in Wisconsin then 2c – 67 or c+5would equal the number of counties in Oklahoma. Although the problems in Tier 2 and Tier 3 are more complex, the same steps and thought processes are followed when creating the answer choices.

Justifying Equivalence Using the Properties of the Operations

Once students have a grasp on what these more complex algebraic expressions look like, they will be introduced to manipulating them using the rules of arithmetic. These rules are also known as the Properties of Operations. They give us a clear understanding of the formal properties of the operations, addition, subtraction, multiplication, and division, and why manipulations work better with some of these operations than others. These rules also allow the students to understand that when certain rules are applied, alone or together, an expression can be transformed into a different, but equivalent one. Usually in the classroom, students are given these sets of rules as a list that shows them how to perform them in order to create equivalent expressions but never go into detail as to why it all works. To clear up these misunderstandings, this unit will be focusing on the “why” aspect of the rules.

In order to explain the Rules of Arithmetic, which are listed in Appendix 2, I will attempt the same strategy as is used to simplify expressions in a math problem. Before getting into the “why” we must first introduce the proper vocabulary that will be addressed in this section of the unit. They include the Commutative Rule, the Associative Rule, the Identity Rule and the Inverse Rule for each operation (i.e., addition and multiplication) and the Distributive Rule that connects the two.

The Commutative Rule of Addition is a rule that students know to be true, but might not officially know it as being the Commutative Rule. It explains that when we add any two numbers, we can reverse their order and still get the same answer. This is the same for the Commutative Rule of Multiplication, any order we multiply two numbers, we get the same answer, for example if we multiply 10 by 5 that will give us 50. If we multiply 5 by 10, we will still get 50. Since they both give us the product of 50, it can be written that 10∙5=5∙10.

The next rule to be discussed is the Associative Rule. It states that when adding three numbers, if we move the parentheses to change the numbers that will be added first, we can still get the same result. For example, if we add 9, 7, and 3, we can group them as follows, (9+7)+3. To solve this, we must add 9 and 7 first to get 16 then add 3 to that sum which will get us 19. If we must the parentheses to add 7 and 3 first, then 9 to that sum, the new expression would be (9+7)+3. The sum of the numbers in the parentheses would be 10 and after adding 9 we will also get 19. This shows us that the two expressions are equivalent, (9+7)+3=9+(7+3). This is also true when multiplying three numbers.

Once my students understand the Commutative and Associative Rules of Addition and Multiplication, I will introduce them to the Identity Rule. The Identity Rule of Addition states that when we add any number to 0, we get the same number because adding a number to 0 does not change the value of a number. The Identity Rule of Multiplication states that when we multiply any number by 1, the value doesn’t change.

The next Rule of Arithmetic is the Inverse Rule. This rule states that while working with the operation of addition, we must find its inverse or its opposite and add them together. In the case of addition, the opposite of a positive number, 10 would be its negative, -10 and when we add them, we would get 0. With the multiplication rule, we must do the same, find the inverse of a number and multiply the two to get the result of 1. The inverse in the case of multiplication is the reciprocal, which introduces fractions. For example, if we have the number 6, its reciprocal would be 1/6 and we know this to be true because when multiplied, the product is 1:  1/6×6=1. From this rule, we are able to use subtraction and division where necessary.

The final rule that students will learn is the Distributive Rule, which involves a combination of addition and multiplication. A clear understanding of the Distributive Rule is necessary because students often times are unsure of what it means to distribute a number. If this remains the case, as we get to the algebraic expressions, students will become discouraged because they will not always be able to deal with expressions involving multiplying a sum in parentheses, this will throw them off and cause many issues. Students incorrectly want to multiply the specific number with the first term, but not the second, which causes them to come up with an incorrect answer.

The symbolic statement of the Distributive Rule is, for any numbers a, b, and c, a∙(b+c)=a∙b+a∙c. This canbe illustrated with the area model of multiplication in Figure 2. It is visually clear that this area model has 3 rows and the columns are split into two sections, one of 4 units and the other of x units. To find the total number of square units of this model we can find the area, LW, of each section. For the first section, we would multiply x and 3 to get x∙3 or 3∙x as the area. In the second section of the rectangle, we would multiply 4 and 3 to get 4∙3 or 3∙4. The total area in this case would be found by adding the area of the first section and the area of the second section, (3∙x)+(3∙4). Finally, through the Distributive Rule, we can factor out the 3 to get 3∙(x+4) which means that 3 should be multiplied by the whole sum of x+4.

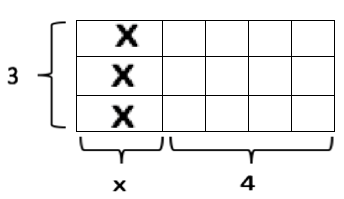
Figure 2

The questioning method in this section will follow the same process as when students were translating expressions. The questions will be tiered for each Rule of Arithmetic. Tier 1 will be only numerical expressions, Tier 2 will be algebraic expressions, and Tier 3 will be a combination of the rules. This allows students to gradually understand why the rules operate the way that they do. The problems for Tiers 1 and 2 can be referred to in Classroom Activities.

Tier 3 is not specific to any one rule. It will include problems that incorporate different combinations of the rules of arithmetic. To build students up to expressions that look more complex, there must be a progression of problems. The table below shows this progression.

If we look at the problem in the “Basic” column visually it is much simpler than the other two. The question that would be asked of the students would be to name the rules that would be used to transform the given expression to an equivalent expression in standard form, ax + b, using the Rules of Arithmetic and it would be answered in the following way:

Beginning with (u + 5) + u, the students should be able to notice that they should get the variables next to each other in order to add them together, but there are parentheses that should be moved first using the Associative Rule of Addition. After moving the parentheses, students will have u+(5+u). The variable and 5 should then be switched by using the Commutative Rule of Addition, to get u+(5+u). Once the variable and 5 are reversed, they must use the Associative Rule of Addition in order to group the variables together, then the Identity Rule and Distributive Rule to obtain(1+1)u . Finally, once they add the coefficients in the parentheses they will get the final expression 2u+5.

This method, of having students show their step-by-step process will allow for them to quickly simplify expressions in the later section because they will have understood how to manipulate complex expressions using the rules. By teaching why we must properly apply these rules to expressions rather than simply teaching our students how to apply these rules, students will be able to catch their mistakes before they make them. This is where the semantics, meaning, take over in the classroom with the syntax, how to solve a problem, backing it up.

This example also illustrates that there are multiple Rules being used even in this relatively simple type of problem. As the expressions get more complicated, it becomes more and more tedious to just use one step at a time. There is a more efficient method that students will be able to use called the Any Which Way Rule. This rule allows students to manipulate expressions that need to be simplified and includes multiple applications of the Associative and Commutative Rules of Addition. If there are one or two sets of parentheses and any number of terms being added together, this rule allows us to reorder the terms and parentheses to have the like terms together to be added at one time.⁶ For example in the example above, students would be able to go directly from (u + 5) + u to (u+u)+5 using the Any Which Way Rule. Similarly, they could convert a more complicated expression, such as (3x+5) + (4x – 3) directly to (3x+4x) + (5 – 3).

Simplifying Expressions

As students have received practice on using the rules of arithmetic and understanding how and why they have worked in the previous section, they will begin simplifying these algebraic expressions. Through this process of simplification, students will take any combination of linear algebraic expressions and manipulate them through addition or subtraction to get them down to one equivalent expression in the standard form of “ax + b” where a and b are specific numbers. In this section, it will be important that I focus on explaining why certain terms can be combined while others cannot. There is a common gap in student understanding during this section of the unit, because many of my students do not know how to apply these rules that they had to memorize when simplifying complex expressions. This is where the “conjoining” will occur and students’ thought processes must be heard out so that I can properly allow my students to grow as mathematicians. I will talk them through the reasoning behind why the new expression is equivalent to the compound expression by referring back to the vocabulary that they learned in the beginning and previous lessons. This is crucial in order for them to be able to support their reasoning correctly. This will ensure a clear understanding of the language of mathematics, especially as they build on their ability to speak about math.

An example of a problem they would have to simplify in this section would be -3/4 (4k-8)+ 4/3 which could be done in the following way:

Students would begin by using the Distributive Rule to multiply 4k and 8 by - ¾ in order to remove the parentheses and be able to combine our numerical terms. After distributing, we end up with an equivalent expression (3) where, through the Associative Rule of Multiplication, we move the parentheses to multiply -3/4 ∙4 and get -3. We must then multiply -3/4 to 8 which is equal to -6. Since we will be subtracting -6, through the “Definition of Subtraction”⁷ when we subtract a negative, it means we will be adding 6. Now that the parentheses were properly removed, we are able to combine our terms that are alike to get to the expression in line (7). To check and ensure that they have gotten the correct answer, students should substitute any number for the x of the original expression and the x of the simplified equivalent expression, and verify that they get the same value.