Big Numbers, Small Numbers

Content Objectives

This 2 to 3-week unit is designed to focus on having my students correctly interpret, use, and compare base ten numbers, especially decimal fractions. Arithmetic will not be covered directly in this unit. In “Place Value as the Key to Teaching Decimal Operations,” Judith Sowder explains,

More recent research on decimal-number understanding confirms that many students have a weak understanding of decimal numbers. […] The children in these studies were primarily from classes where the introduction to decimal numbers was brief so that sufficient time would remain for the more difficult work of learning the algorithms for operating on decimal numbers. But time spent on developing students' understanding of the decimal notation is not time wasted. Teachers with whom I have worked claim that much less instructional time is needed later for operating on decimal numbers if students first understand decimal notation and its roots in the decimal place-value system we use.⁶

In my experience, this is true. It has also been my experience that reteaching my students anything, is challenging, and reteaching students how to operate on decimal numbers in deep, meaningful ways is no exception. My students are often reluctant or angry when they must relearn what has already been taught, and what they thought they already knew. This unit will attempt to alleviate some of the reteaching and frustration that may usually occur when working on operations of decimal numbers.

The topics in this unit will follow the Pennsylvania Core State Standards, the Assessment Anchors and Eligible Content Aligned to the Mathematics Pennsylvania Core Standards, and the Pennsylvania Core State Standards for Mathematical Practice Standards (see Appendix), but the standards are very similar to the Common Core Standards. Additionally, the topics will address the Pittsburgh Public School District’s Scope and Sequence. The unit is divided into two sections:

• Understanding the base ten place value system
• Comparing Decimal Numbers

Because I feel it is important for students understand where math, and all subjects, fit into their lives, this unit will also empower and elevate 5^th grade students’ conceptual understanding of decimal place value by:

• Being culturally responsive;
• Implementing goal setting using pre-assessment data;
• Using concrete representations such as base-ten blocks, straws, and meter sticks;
• Using visual representations such as hundredths grids and number lines;
• Using abstract representations such as place value charts;
• Differentiating instruction in small groups to ensure mastery;
• Completing a culminating project-based learning activity and post assessment;
• Using portfolios.

By the end of this unit, students will be able to:

• Explain and illustrate, in various ways, how a digit in one place represents 10 times of what it represents in the place to its right and 1/10 of what it represents in the place to its left, using place value charts, hundredths grids, and meter sticks. (With adjacent digits such as 6.55 and in separate numbers such as 6.15 and 5.61).
• Read and write decimals to the thousandths using base-ten numerals in various forms including, word form, and expanded form (using decimals, recognizing the multiplicative make-up of the place value pieces in decimal form and decimal fraction form).
• Compare two decimals to thousandths using the comparison symbols >, =, < to record the results of the comparisons.

Understanding the Base Ten System

The key to understanding the base systems is realizing that digits “roll over” like a clock or an odometer when they are full. Our decimal system is Base Ten, meaning that it uses a system of units, each of which is ten times as large as the next smallest one, and conversely, one tenth as large as the next largest one. Consequently, we never need more than nine (one less than ten) of any unit to express a number. When we get to ten of any given unit, it “rolls over” and creates one of the next larger units. Our method of measuring time is similar, but with time, we wait 60 seconds before “rolling over” to a new minute.

Back in the day, Babylonians used base 60 and Mayans used base 20, but base 10 is what we use today. Perhaps because we have 10 fingers. The Egyptians, Greeks and Romans also used base ten, but they did not have the idea of place value, in which the position of each digit indicates the unit is multiplying. The Egyptians and Romans had a separate symbol for each of the first few units. The Greek system was very limited and used their alphabet.

The base ten system is also known as the decimal system. Although the concept is not simple, the system is simply a way of writing numbers. It is called a positional system because each place value increases by a factor of 10 from the place to the right! Prior to developing this unit, I did not know the decimal or base-ten place value system was based on the Hindu-Arabic derived symbols for the digits: 0,1,2,3,4,5,6,7,8, and 9. It was introduced in Europe around the 12^th century, and because it was such an organized way to work with numbers, that allowed for counting and calculations in a more efficient way, it replaced the Roman Numerals, which had been the main method for writing numbers. Place value notation is more efficient than Roman Numerals (compare MMXVII with 2018), but the big advantage of place value notation was the way it supported computation, especially multiplication!

The Egyptians used Hieroglyphic writing, which included symbols for writing whole numbers up to 1,000,000. This decimal based system allowed for the additive principle: a number was represented by a collection of symbols whose values added up to the number. This is a way in which numbers can be counted. There was a special symbol for each power of 10. See figure 1 below. To see the Egyptian Base Ten System in its entirety, please go to the notes section.⁷

It is important to mention this historical background here because my students have failed so much that they believe they can’t do math. Even many of their parents and family members make snide comments such as, “I wasn’t good at math either, so I don’t expect him/her to be that good either.” This belief is extremely deep in many African American students, so it’s important to acknowledge the rich history of their ancestors and show that math is already in their blood. Again, I am aiming to empower my students to believe they can excel as young mathematicians, and one way to do this is to include the history of math of their ancestors and other multicultural aspects of mathematics. In the movie, Stand and Deliver, Jaime Escalante held a high conviction in his students, saying that mathematics was in their blood because their ancestors, the Mayans, were the first to conceptualize the idea of “Zero.” Because he believed in them, and showed them who they were, his students believed in themselves and achieved at high levels.

Figure 1.

The difference between the Egyptian Base Ten system and the Hindu-Arabic System is that the Egyptians did not have a positional system. In Egyptian hieroglyphics, each power of ten was represented by a different symbol, whereas 0 played a key role in specifying clearly the positions of the digits in the Hindu-Arabic System. The Base Ten positional system means that the position of a digit gives its place value. This system was extended from whole numbers to include decimal fractions by Islamic scholars in the 10^th century. For example, a typical person in the community where my school is located might have a yearly income of $ 28,927.25. A student in 5^th grade should be able to explain the value of the digits in a decimal fraction, such as the number above. For example, a fifth grader should know that the 2 at the left of that number represents $ 20,000 = 2 × $ 10,000, but the 2 just to the right of the decimal point represents only 2 tenths or a dollar or 2 dimes, or 2 × 0.1, or 2 × 1/10. They should also be able to explain that the two in the ten thousandths place is 100,000 times larger than the two in the tenths place or that the two in the tenth place is 100,000 times smaller than the two in the thousandths place. Each digit has an explicit value that is determined by its place in the number, and each adjacent digit that is the same is larger or smaller by some power of 10. A major part of the unit, these concepts will be address in every lesson within the unit as well as operations with decimal numbers and decimal fractions later in the year.

The Five Stages of Place Value

This unit will emphasize the five stages of place value as described in by Howe-Reiter.⁸ The stages can be summarized in the sequence of the equivalences below:

625

= 600 + 20 + 5

= (6 x 100) + (2 x 10) + (5 x 1)

= 6 x (10 x 10) + (2 x 10) + (5 x 1)

= (6 x 10²) + (2 x 10¹) + (5 x 10⁰)

The first stage is what we refer to as the standard form of a number. The second stage recognizes what we call expanded form, and exhibits the number as a sum of pieces, one for each digit, which we will call place value pieces. The third stage can be referred to as the second expanded form and recognizes the multiplicative make-up of the place value pieces. In this case, you can see the base ten units, namely 1, 10, and 100 in this example, being multiplied by non-zero digits. The fourth stage is a stage that often gets left out of textbooks and perhaps many classrooms including mine. But this stage recognizes the multiplicative make-up of the base ten units as a power of 10, or tens being multiplied repeatedly. Lastly, the fifth expression illustrates the structure using the exponential notation for powers of 10. In Pennsylvania, all 5^th grade students are expected to interact with each stage based on the PA Core Standards. Focusing on the Five Stages of Place Value will give students a strong background in place value because it allows them to get to know the numbers as made of pieces and to really understand the patterns of the base ten system and the powers of ten. This unit will discuss the first four stages but will leave the fifth stage for later grade as negative exponents are not a part of the state standards. This concept will be addressed and practiced in lesson 5.

Place Value

Like the whole number system, the full decimal system uses place value meaning that the place in which a digit is located determines the value of the decimal number. For example, the 3 in 3.19 stands for three ones, but the 3 in .63 stands for three hundredths. Each digit has a place, and that place determines the value of the digit, or how much it is worth. The chart below shows the value of the decimal places between one thousandth and one million.

Table 1.

It is a challenge for many students to correctly translate between word form and decimal numbers. For example, in the number 3.19 a student may say and write three point one nine or three point nineteen which is the literal translation of the symbol instead of the word form signifying the value for three and nineteen hundredths, or three ones and one tenth and 9 one hundredths. Students are unable to understand the full meaning of positional notation. Many adults use the literal translation as well, but it does not allude to place value, which is important when doing calculations and operations with decimals. I will do my best to correct this misconception by naming the values consistently, accurately, and often, to reinforce the place value and ensure my students do so as well. Students need to verbalize each digit as it relates to the order of magnitude. Another important aspect is the word and. It must be used to show the decimal point in a mixed number.

Decimal Numbers

Decimal numbers are an extension of the whole number system, in which negative powers of ten, which represent proper fractions, are separated from the positive powers, which represent whole numbers, by the decimal point. The decimal point is a symbol that allows the base ten system to express parts of numbers. When describing quantities that have parts less than one, we call them decimal numbers, or decimal fractions. Students are introduced to three new places on the right of the decimal point by fifth grade: the tenths, hundredths, and thousandths places.

Lesson 3 will address how some students can infer and then continue the pattern to smaller decimal places. This is because each place follows the same word pattern of the base ten number system. Meaning that, after they learn about the tenths, hundredths, and thousandths, students may understand that ten thousandths, hundred thousandths, millionths, ten millionths, etc. will proceed. However, this does not mean that the student understands the multiplicative pattern of repeatedly multiplying or dividing by 10. In other words, students may not understand that “each place’s value is ten times the value of the place to its right,” or 1/10 the value of its place to the left.⁹ As a digit moves to the right of the decimal point in a number, the value of each place is divided by 10 or multiplied by 1/10. It is beneficial to imbed this concept into a problem-solving activity. Cognitively demanding tasks that require students to explain their reasoning is an instructional practice that is beneficial for all students.

Comparing decimal numbers should be easy, but when it comes to comparing or even ordering them in racing something interesting happens. Students assume the person with the largest number wins the race. But in racing the smaller number is the winner. A good way to illustrate this concept is through an actual race which lesson 8 will address. Many students will visually and physically see who won the race and know how to order the numbers based on what they have witnessed. Some students will have a difficult time recording and analyzing the times even though they saw the race. Regardless of how students determine the order, it is imperative for my students to learn to compare each place with the same place in the other number(s) and understand that the largest place is the decision maker.

Decimal Numbers and Money

Decimal numbers can be represented in many ways. Children are often aware of them because they have some experience dealing with money. Money is very relevant to my students. Having it means they can get what they want and need to survive. Not having it means they may suffer or perhaps end up hungry and homeless. The value of money can be large, and the value of money can be small. But most students know they need money to get the things they want and need to survive. Simply put, money makes sense (pun intended). But it didn’t always.

Money is a great way to “storify” this unit and connect to the past. Between bartering with objects, salt, silver, gold, cloth, cowry shells, animals, etc., an easier currency was bound to be developed. No one wants to carry a baby goat in their pocket. But my students know what it means to trade things. According to Richard Pankhurst in “An Introduction to the Economic History of Ethiopia,” “The earliest example of coins minted in Africa comes from the kingdom of Axum, which struck money from the 3rd until the 8th century CE.”¹⁰ This is pre-slavery. Our school curriculum does not often discuss Africans before slavery. My students need to know that their ancestry is rich! My students have stereotypes about what Africa is and is not, and many believe that is a poor region. I have heard negative attitudes and misconceptions shared in the classroom, and believe it or not, I had those same perceptions as a child. Typically, the math in the U.S. is presented in public school materials as the exclusive creation of men from European ancestry. But through my research, I learned the lattice multiplication method was introduced to Europe by Fibonacci. Although he was not the only, he was a major source for the use of the decimal system. He was an Italian mathematician who learned how to use Arabic numerals from a Moorish (African) teacher in Bugia, located in Algeria, in Africa. I will certainly share this knowledge with my students!

While money is familiar to many students, it is not the only way decimals can be represented. Physical representations of decimals using base-ten blocks, meter sticks or other number lines really help students understand the concept of decimal number units of measure. Lesson 4 will feature money examples.

Metric System

Did you know that the United States is only one of three countries in the world that has not adopted the International Metric System?¹¹ I feel that if I do not take the time so teach my students about the metric system, it will do them a great disservice as they grow to explore the world. Focusing on length in lesson 6, I will introduce my students to the metric system, and share that only the countries of Burma, Liberia, and the US, are the only three countries in the world that have not converted. Imagine how difficult traveling can be when you visit another country without this background knowledge! The metric system is a natural way to help students understand place value and number lines in a concrete way. Also, measurement is a skill that our students struggle with, and do not have a lot of time to study due the time of year in which it is introduced. I feel that if some of the basic concepts of the metric system are taught earlier and included within another standard, students are more likely to remember. Table 2 below illustrates the metric units of length. It uses a place value chart which my students will already be familiar with, as well as the mnemonic device, “King Henry Does Usually Drink Chocolate Milk,” to help them remember how to convert units.

Table 2

Conceptual understanding that connects the notation with the value being represented is key for students to fully grasp decimal numbers.

I will encourage my scholars and young budding mathematicians to think and ask questions such as, “How can I make this easier to deal with?” Generally, mathematicians look for ways to make complicated ideas easier and more familiar for them to deal with.

Expanded Form

The expanded form of a number shows the value of each digit in a number when in a place and decomposes each non-zero digit to represent a sum. For example, let’s consider the following: A gallon of gas at Sunoco costs $3.249. Model this number using base-ten blocks. Then write this number in word form, standard form, and the two expanded forms.

This is a typical problem a student may need to answer. Students in fifth grade are not required to write exponential notation of decimals which result in negative exponents. The value of these digits is 3.249 and can be understood to represent a sum:

3.249 = 3 + .2 + .04 + .009

The expression on the right side of this equation is the expanded form of 3.249. Each number uses the place value system, which means to place a zero in the places where the non-zero digits are located. When writing numbers in expanded form, students often have some misconceptions especially when it comes to fractional parts. They may show this number in two different ways. One way is 3,000 + 200 + 40 + 9. If a student records the number this way, they are disregarding the decimal point and reading these digits as whole numbers instead of a decimal number.

To guide a student that disregards decimal points, it would be helpful to ask them about it. I would ask these series of questions during small group time when I provide differentiated instruction to my students. Do you see a decimal point or a comma? Can you read this number to me? Read it out loud to me. How much money would this be? Can you use base ten blocks to create this number? I would have the student build the number. Which base ten block represents ones, tenths, hundredths, thousandths? Can you show me how to represent this number using money? How may dollars, dimes, and pennies? How come the nine cannot be represented using money? Can you write these digits on a place value chart? What is the value of each digit? How many ones, tenths, hundredths, and thousandths did you write in each place?

Students also have another misconception once they become aware of the decimal point. They will write and recognize that three is a whole number, but two tenths, four hundredths and nine thousandths may be written in the same place. For example: .2 + .40 + .900 instead of 0.2+ .04 + .009. While they are now aware there is a decimal point, they do not understand that each digit has its own special name and place. They believe that these digits have the same quantity or order of magnitude. When digits have the same order of magnitude, they are said to have the same quantity of “powers of 10” that there are in a number. For example, the misconception of the value of the digit 4 in the number 3.249 has a value of 0.4 = 4/10 and has a magnitude of 4 x 1/10 = (4 x 10^-1) and the actual value of the 4 in the given number is 0.04 = 4/100 and has a magnitude of 4 x 1/100 = (4 x 10^-2). The difference in the order of magnitude in these two numbers is 1, and 0.4 is 10 x greater than 0.04. 

This misconception stems from students work with whole numbers, and the belief that all one must do to write a number in expanded form is to annex zeros to the non-zero digit. This is another reason why word form and patterns must be emphasized and practice with models must occur.

Expanded form does not stop here. In fifth grade, students much be able to decompose numbers even further. In this second version of expanded form, students are essentially breaking the numbers down into base ten pieces. Students should be aware of the identity property at this time meaning that if a multiplicand is 7 and the multiplier 1, the product will be 7. In other words, the product of any number multiplied by 1 is always equal to the given number. With that, I want my students to have experience with knowing 10 x 7 = 70, 100 x 6 = 600, but also that 0.2 = 1/10 x 2 and 0.04 =  1/100 x 4. I want my students to realize that the number of zeros in the standard or expanded form of the units tell you the value one should multiply by.

Using the approximate cost of gas mentioned above, here is the second expanded form using multiplication:

3.249 = (3 × 1) + (2 × 0.1) + (4 × 0.01) + (9 × .001)

Please note the following equivalencies

I will develop and expect my students to be able to write and read these equivalences. Another version of expanded form explains how many times to repeatedly add unit fractions based on the non-zero digits in the standard or first version of expanded form. Showing students this version will help them connect what they already know about the relationship between repeated addition and multiplication. It is always important to recognize and build on children’s background knowledge and strengths. I will also explain that due to its length, we rarely want to write expanded form in this way.

3.249 = (1 + 1 + 1) + (1/10 + 1/10) + (1/100 + 1/100 + 1/100 + 1/100) + (1/1000 + 1/1000 + 1/1000 + 1/1000 + 1/1000 + 1/1000 + 1/1000 + 1/1000 + 1/1000)

When my students learn material and are engaged in various ways, they retain math content for longer periods of time. Last year, paper airplanes were a huge disruption across our building. Sometimes when you can’t beat the kids, you join them! To “gamify” the unit and connect it to the present, I will have students create various paper airplanes, and measure the distances they fly. Each student would need to measure the distance writing the standard form, word form, and expanded form to the nearest hundredth of a meter (i.e., nearest centimeter). This allows students to use real measurements, be physically active, and apply what they have learned. Let’s say one of the paper airplanes flew 3.19 meters in length. I want my scholars to visibly see that it flew three whole meter sticks AND 1 whole decimeter (or 1.10) of the next meter stick, and 9 centimeters of the next decimeter (or 9/10)  of a dm or 9/100 of the meter).

In other words, the expanded form of 3.19 = 3 + 0.1 + 0.09

Which is 3.19 = (3 × 1) + (1 × 1/10) + (9 ×1/100)

Number Lines

Number lines can be very helpful for students. As a matter of fact, number lines are an abstract form of length measurement! In this section, I show just how. For example: In lesson 6, we all flew airplanes and measured the distances each plane flew. It was easy to see which plane flew the furthest or shortest distance based on where they landed in the hall and if you saw where it landed. What may not be so easy is if the numbers are close in numerical value, and you were not in the same group as someone with that value. I will choose two numbers from our airplane list to compare. The first student’s plane flew 2.7 meters. The second student’s plane flew 2.65 meters. Whose plane flew the furthest? Using number lines in lesson 7 will help students see how meter stick are concrete number lines, therefore making another connection go the students and building upon what they have already learned.

Many students have a misconception that the longer the number is, the larger it is. This comes from their experience with whole numbers. A student that believes this would say the second student’s plane flew farther than the first student’s plane because 2.65 has more digits than 2.7.

I want my students to understand that decimal numbers “fill in” sections on the number line between whole numbers. On the number line below, the whole numbers 0 through 10 are represented. Some students do not realize there are decimal numbers between whole numbers. “You can think of plotting decimal numbers on the number line in successive stages.”¹² On this number line, the first stage consists of the consecutive whole numbers from 0 through 10. This would represent the ten meters for our problem. Students would need to estimate where the numbers are to plot them on the number line. Because 2.7 and 2.65 are both greater than two, we would want the student to plot them after two but before three.

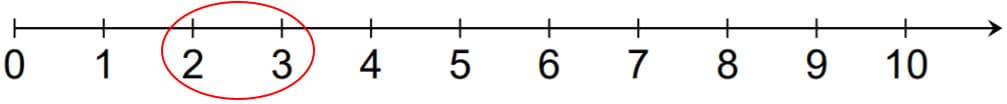
Figure 2.

Let’s take a closer look at this same number line by “zooming in” to the whole numbers 2 and 3 with the tenths marked. Why? Because the students that jumped have measurements that are between two and three. Almost immediately we can plot student 1’s measurement of 2.7 meters. It is a little more challenging to see student 2’s measurement of 2.65. Another important thing to mention is although intervals between the digits 2 and 3 are broken into 10 sections, there are only nine tick marks for the decimal numbers. Digits in the base 10 system “roll over” after 9.

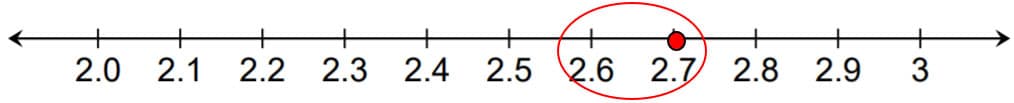
Figure 3.

Let’s “zoom in” again. Where? Because 2.65 is greater than 2.6, we will “zoom in” between 2.6 and 2.8 to show the hundredths between 2.6 and 2.8 so students see that all the places between whole and decimal numbers need to be broken up into 10 equal pieces which creates new decimal numbers in between the points previously plotted. Once the hundredths have been plotted, it is easier to see where each number is located on the number line.

Figure 4.

At each stage in “filling in” the number line, we break each interval into 10 equal pieces which then displays new decimal numbers in between the points previously plotted.  A good point to make to students is that like whole numbers, decimal numbers are also infinite. In fact, there are an infinite number of them in any interval, no matter how short! By breaking the meter stick or number line down into sections, this will show that the pieces are shrinking. By comparing the two numbers on the number line, a student is able to see that 2.7m is further away from zero than 2.65m is and therefore, able to show the first student’s plane flew farther than the second student’s plane; 2.7m > 2.65m. Decimal numbers do not only “fill in” number lines. They also represent distances from zero. This is important because we do not want our students to develop the misconception that decimals are less than zero. While there are negative decimal numbers, fifth grade students are only required to work with positive numbers.

Ordering Decimals

Although ordering decimal numbers is not included in the 5^th grade standards for my state, I feel that it is a necessary skill for students to know. Therefore, the first part of this lesson will help to develop that concept. I will “gamify” this lesson by “mak[ing] it social.”

Once these place value concepts have been addressed and hopefully mastered by students, they can then be applied to show an understanding of operations as they pertain to whole and decimal numbers. It is important to note that I do not plan to have students do arithmetic in this unit. Immediately following this unit, I will teach a unit on adding and subtracting decimals, with multiplication and division of decimal numbers occurring later in the year.

Children often think there are no numbers smaller or less than one despite maybe carrying change in their pockets, seeing an ant on the ground, or even eating one slice of pizza out of a box. We encounter small numbers and decimal numbers every day when we see the prices of items such as $3.19. However, the conceptual understanding of decimals requires students to connect decimals to whole numbers and to fractions. Prior to teaching this unit, I will have taught a unit focused on whole numbers. I want my students to see the magic and power of the base ten system and how a good understanding of numbers and mathematics can prepare them for the world and life outside of school.