Big Numbers, Small Numbers

Classroom Activities

This unit will be composed of eight lessons. They are:

Lesson 1: What do I know about decimal numbers? (1 day)

Lesson 2: Little Numbers: Comparing Adjacent Digits (1-2 days)

Lesson 3: Little Numbers: Comparing Adjacent Digits within in Word Problems (Day 2)

Lesson 4: The Five Stages of Place Value (Making a Reference to Money) (1 day)

Lesson 5: Reinforcing the Five Stages of Place Value (2 days)

Lesson 6: Using Meter Sticks to Measure the Distance Paper Airplanes Fly

Lesson 7: Comparing Decimal Numbers Using Number Lines (1 day)

Lesson 8: Who wins the race? Cumulative Review/Project (2-3 days)

I have included sample plans that I will use for each lesson below including the objective, materials, procedures, and closure.

Lesson 1: What do I know about decimal numbers?

Objective: Students will: share what they know about place value and decimal numbers using The Graffiti Wall Strategy; participate in a class discussion; complete a pre-assessment.

Materials: Markers. Same group, same colored marker so I can ensure each student has participated from each group. 5 large Post-It posters hanging in the room with the following 5 statements or questions:

• Write any number less than one. Any number less than one is acceptable, but it is important to focus on decimal fractions, and students may need guidance.
• Show as many ways as possible to represent 214 (my homeroom number). Accept non-standard as well as standard ways. Allow students to share their knowledge and creativity, but the primary focus is standard ways of representation.
• Where do you see numbers in your community? List as many places as possible.
• What do you know about decimal numbers?
• The year is 2018. Which is the easiest way to write 2018? I will write 2018 on one of the posters using the Hindu-Arabic Numerals, Hieroglyphics, Hieratic Numerals, and Roman Numerals.

Procedures:

1. Students will be broken into groups of 4-5 students and given the appropriate marker and sent to a poster.
2. Students will have about 3-5 minutes to discuss and respond to the prompt/question.
3. After time expires, students will rotate to the next poster. This time, they can respond to the prompt/question OR respond to a comment left by the previous group.
4. Students will continue rotating until all the groups have visited the posters.
5. Students will return to their seats and the posters will be used to guide a class discussion.
6. After the discussion, students will complete a pre-assessment which will allow me to see where my students are, what they need, and where I should begin. The data I glean from this pre-assessment will allow me to differentiate learning in small groups and my scholars and I to set worthwhile goals. The pre-assessment data will be added to their portfolios.

Closure: Exit ticket. I will use one of the templates in the resources below.

Lesson 2: Little Numbers: Comparing Adjacent Digits (1-2 days)

Objectives: Students will: listen to me read the book, “Little Numbers,” and answer comprehension questions related to vocabulary words and events taking place in the story regarding what is happening to the main object: the dinosaur; understand that a digit in one place represents 1/10 of what it represents in the place to its left: be able to explain that as a digit moves further away from the decimal to the right, the value of the digit is being divided by 10 OR “shrinking” by a factor of 10 using base-ten blocks (Figure 5), a number line (Figure 2) and a place value graphic (Figure 6).

Materials: The book, “Little Numbers.” A bundle of 100 straws, already grouped into smaller bundles of 10. (This will be from an activity we completed earlier in the year with whole numbers when showing how each place gets exponentially larger than one by a factor of 10 for each place to the left of the decimal point. We will have also read “Big Numbers,” also by Packard). Base-ten blocks.

Procedures:

1. Activate prior knowledge of whole numbers: Students will play a game of “Would You Rather…”

1. Would you rather have $ 0200 or $ 2000?
2. A discussion would follow on why and what about the numbers makes them think one number is larger than another.
3. How much greater is that number than the other?
4. Teacher will show both numbers using base ten blocks. How many flats make a cube? (10) How many flats make two cubes? (20) (This figure shows how this unit will use base-ten blocks to represent decimal numbers.) Base ten blocks are another way student can manipulate the value and size of numbers. Most teachers have plastic sets of base-ten blocks that can be used to represent whole numbers, but they can also be used to represent decimal numbers. I did not always know this.

Figure 5.

2. A portion of following figure will be drawn on the board. (The ones to the millions place and no division.) This will be to remind the students of the multiplicative patterns of the place value system.

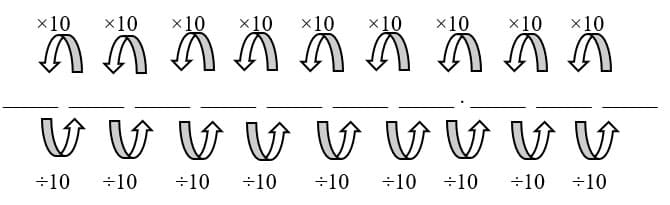
Figure 6.

3. Introduce new concept. Read “Little Numbers.”

4. We know there are decimal places that are not whole numbers. If the relationship is to multiply by a factor of 10 to get to the next place value to the left, what relationship, or what happens mathematically as you move to the to the right in a number? (Students will only see arrows, but no division symbols at this point.)

5. Show one strategy for determining the relationship between places moving to the right of the decimal point by looking at a whole number and modeling it with the straws. I will write all numbers on the board using the model, so the students can see that the numbers are shifting their place and value.

6. Separate the 100 straws back into groups of 10. What is the value of the straws I am holding now? (10)

7. Separate the straws that are in groups of 10 into 1 straw. What is the value of the straws I am holding now? (1) What is happening to the value? (The value is shrinking.) By how much each time? (10)

8. How I show the next place value using this one straw? (Cut it.) Into how many pieces? (10.) Why ten? (Because each place is getting smaller by 10 as you move to the right of the place value model). I will physically cut the straws.

9. What mathematical operation is occurring for this “shrinking” to happen?

10. Show another strategy modeling with base-ten blocks for determining the relationship between places moving to the right of the decimal point by looking at a whole number.

11. We will use 333 to model this using the place value graphic and base-ten blocks. See Figure 3.

1. What is the value of the digit in the hundreds, tens, and one’s place? Write the values.
2. What happens, mathematically, to the value of the digit as it moves to the right from the hundreds place to the tens place? (The tens place value is exactly 10 times smaller than the hundreds place value for the same digit. Students should also explain that 300 divided by 10 equals 30, and I will write this on the board.

12. The same line of questioning will occur with the next example, 7.77. The value of the base-ten blocks will change, and this will be emphasized with an anchor chart I will create using Figure 5. We will keep in mind that the goal is for students to understand and explain that the value of the place to the right is 1/10 or 10 times less than the place to it’s left.

13. Another example may be needed. This will be based on time, student engagement, and student understanding.

14. Following the introduction of the new concept, I will allow students to work with the place value concept in small groups or with a partner by completing task cards. While the students are responding to the prompts and questions of the task cards, I will conduct formative assessment and facilitate learning by providing feedback and asking clarifying and probing questions.

Closure: Exit slip: Students will fill in the following blanks: When digits shift to the right of the decimal point, it is like they are _________ (“shrinking.”) When the dinosaur grew smaller from 1.0 to 0.1. How many times smaller did it become? (10 times smaller).

Lesson 3: Little Numbers: Comparing Adjacent Digits using Word Problems – Day 2

Objectives: Students will: be able to understand that a digit in one place represents 1/10  of what it represents in the place to its left; be able to explain that as a digit moves further away from the decimal to the right, the value of the digit is being divided by 10 OR “shrinking” by a factor of 10 using base-ten blocks (Figure 5) and a place value graphic (Figure 6).

Materials: Base-ten blocks, place value graphic, problem solving activity.

Procedures:

1. Using examples like the task cards from yesterday, students will review decimal place value patterns.
2. Students will be broken into 3 groups for differentiated instruction. For 15-20 minutes at a time.
   1. Online individualized learning.
   2. Vocabulary terms will be added to journals.
   3. Problem solving activity with teacher.
      1. Problem Solving Activity: Heaven and Jayden were arguing about the size of two numbers. Heaven thought seven-tenths was ten times larger than seven-hundredths. Logan thought seven-hundredths was ten times larger than seven-tenths. Who is correct? Show and explain how you know. Make sure to refer to place value in your explanation.
3. Students will return to original seats. Students will share out one thing they learned, and one thing they still want to know more about.

Closure: Exit slip will be vocabulary based.

Lesson 4: The Five Stages of Place Value (Making a Reference to Money)

Objectives: Students will: be able to use base-ten blocks to model, read, and write decimal numbers in word form (base-ten numerals), standard form, and the two expanded forms (decimal and fraction). For this unit, the 5^th stage of place value will not be taught.

Materials: Base-ten blocks, place value chart, anchor chart illustrating coin images and values places on a place value chart, as well as a five stages of place value anchor chart both created by teacher.

Procedures:

1. I will refer to a local gas stations’ cost of gas per gallon. This is because gas prices round to the nearest thousandth. A gallon of gas at Sunoco costs $3.249. Model this number using base-ten blocks. Then write this number in word form, standard form, and the two expanded forms.
2. Students will work with a partner to model $3.249 using base-ten blocks.
3. Students will use paper base-ten blocks to cut and paste this model in their journals.
4. Students will use their place value charts to write the digits in each place, and then write the word form. This will also be placed in their journals.
5. Students will use the base-ten blocks to write the expanded form and the multiplicative make-up of the base ten units as a power of 10.
6. Students will model and record several more decimal numbers with a partner. (I intend to use numbers from local grocery stores and corner stores. I will have students bring in decimal numbers they see in their neighborhoods, and/or I will take pictures or use items from a circular to add to a PowerPoint to visually represent the numbers in their world.)

Closure: Exit slip: Students will write the word form, standard form, and two expanded forms of a decimal number.

3.249

= three and two hundred forty-nine thousandths

= 3.0 + 0.2 + 0.04 + 0.009

(3 x 1) + (2 x 0.1) + (4 x 0.01) + (9 x 0.001)

= (3 x 1) + (2 x 1/10) + (4 x 1/10) + (9 x 1/1000)

Lesson 5: Reinforcing the Five Stages of Place Value (2 days)

Objectives: Students will: be introduced to the metric system watching a video; learn an acronym to remember the order of the units in the metric system from millimeters (thousandths) up to kilometers (thousands); be able to use meter sticks to measure the length of the objects in the classroom; connect Metric Conversion chart with the place value chart (specifically rows four and five); record the name of the object, and the length of it using word form, standard form, and two forms of expanded form (decimal and fraction).

Materials: Metric conversion chart, meter sticks, The Story of King Henry video, Venn Diagram, and journals for note taking (the video is told in liters, but the lesson will meters, allow students the opportunity to take notes and remind them to focus on meters for this lesson).

Procedures:

1. Review: How many tenths make one whole? (10). How many hundredths make a tenth? (10) How many hundredths make a one whole? (100) How many thousandths make a hundredth? (10) How many thousandths make a tenth? (100 = 10 x 10) How many thousandths make one whole? (1,000 = 10 x 10 x 10). If we move a digit to the left of the decimal point, one place at a time, is the value of the digit increasing or decreasing? (Increasing) How much larger is the value of the digit? (10 x larger) What operation? (Multiplication) What is happening to the value of a digit as it moves to the right of the decimal point? (Decreasing) How many times smaller is the value of the digit? (1/10 x smaller). What operation can we use to show that the value of the digit is decreasing? (Division if we divide by 10 or multiplication if we multiply by 1/10).
2. Today we will use meter sticks that show this concept. Let’s look at a meter stick.
3. Each group will have a meter stick.
4. This meter stick is one unit long. The unit is a meter. Like our bundle of straws this meter stick has 100 sections called decimeters. Can you see them?
5. Do you notice any other divisions? Do you notice any smaller groups? Look at your meter sticks and discuss other groups that you notice.
6. Students should notice that the decimeters are broken into smaller groups of 10 and these are the centimeters. They should also notice that the centimeters are broken into groups of 10, and these are called millimeters.
7. There are units that are smaller and larger than the units we see, and some measure large things and some measure small things. My question is, how can you remember all these units and what they measure? (Allow for brief discussion.)
8. Share Metric Conversion table. Allow students to compare and contrast it with the place value chart using a Venn Diagram.
9. Watch “The Story of King Henry” video.
10. Students will take notes while watching the video. A copy of the Metric Conversion Table would be good to paste into their journals.
11. After the video, allow students to go around the room measuring and recording different items using the five stages of place value including word form, standard form, and the two expanded forms. (This is NOT a lesson on measurement conversion, so please be careful). The goal is to reinforce the five stages of place value.)

Closure: Exit slip: Write down an example of one item you measured, and include the name of the item, the word form, standard form, and two versions of expanded form. (I will not allow students to use measurements that are whole numbers.)

Lesson 6: Using Meter Sticks to Measure the Distance Paper Airplanes Fly

Objectives: Students will: create paper airplanes; fly paper airplanes; record the distance their paper planes fly in meters, using standard form, word form, and the two versions of expanded form.

Materials: Metric Conversion Chart, Meter Sticks, (a good idea would be to use tape to mark the meters in the hall, gym, or where ever the planes will be flown and allow the students to use the meter sticks to measure the distances their planes fly. My building has an extremely long and straight hall that allows for straight flights, so I anticipate not having enough meter sticks to measure the length of the hall. Chalk is an option if this activity is done outside. Be mindful of wind and rain); paper to fold airplanes.

Procedures:

1. Review the units of the metric system.
2. Teacher will make an airplane and fly it. This will immediately attract students’ attention.
3. Review some ground rules regarding the planes. Planes can only take flight on the runway which is in the hall. Planes may only fly one at a time. All planes are out of fuel once they taxi (land) on the runway and must be placed in the landing zone (a box or bag of some sort).
4. Build Airplanes. Write names on them. Place them in a safe location.
5. It is my goal to have support staff during this lesson. This lesson is intended to be taught in small groups.
   1. Group 1 – Individualized learning on computer or Ipad.
   2. Group 2 – Problem solving activity with support teacher – Problem: Part 1: Tay’s teacher asked him to write 7.835 in expanded form. Tay wrote: 7 + 0.8 + 0.30 + 0.500. What is Mike’s misconception? Use base-ten blocks or a place value chart if for support. Part 2: What is another way to write this number?
   3. Group 3 – Flying airplanes, measuring, and recording distances in hallway with teacher. (All students will remain in the hall until it is time to rotate groups.)
6. All students will record the distances of their flights on a large piece of chart paper from top to bottom, in no particular order. (These numbers will be used in the next lessons on ordering and comparing decimal numbers).
7. Students will return to their seats and record the distances their planes flew in standard form, word form, and the two expanded forms if possible (some students’ planes may be exact whole numbers.)

Closure: The students’ recording sheet will count towards their exit slip for the day.

Lesson 7: Comparing Decimal Numbers Using Number Lines

Objectives: Students will: be able to use number lines to compare decimal numbers; be able to use the comparison symbols, <, >, and = to write expressions.

Materials: Airplane data, open number lines, some closed number lines, dry erase markers and erasers (if you have laminated number lines).

Procedures:

1. Students will discuss what it means to compare two items. Students will compare two whole numbers with a partner. Discussion. How did you determine which number was larger? Which place has the largest value? How much larger is each place as a digit shifts to the left?
2. Students will compare two decimal numbers with a partner. Discussion. How did you determine which number was larger? Which place has the largest value? How much larger is each place as a digit shifts to the left? To the right?
3. We can also use number lines to compare numbers and show which number has the largest value. Using the information from number lines above, will guide this lesson, and can be used as an example.
4. Teacher will choose one or two more sets of numbers from the list and students will work to compare the numbers using number lines. Teacher will take notes as students work and ask clarifying and probing questions as necessary.
5. Students will break into differentiated groups:
   1. Individualized Lessons on computer or Ipads.
   2. Comparing decimal numbers and fractional numbers. Worksheet or task cards.
   3. Problem Solving: Dionne and Don were talking about the numbers 1.253 and 2.351. Part 1: With base ten blocks or number lines, draw a picture of both numbers. Part 2: What is the value of the 2 in both numbers? How does the value of the 2 in the first number compare to the 2 in the second number? Part 3: What is the value of the 5 in both numbers? How does the value of the 5 in first number compare to the value of the 5 in the second number?
   4. Teacher will pull small groups of students to review certain concepts or facilitate the differentiated groups.
6. Students will share one thing they learned or liked in today’s small groups with a neighbor. Three to five students will be asked to share with the class.

Closure: Exit slip: Plot 2 numbers on the same or separate number lines to determine which number is larger. Write a sentence explaining number is larger.

Lesson 8: Who wins the race? Cumulative Review/Project (2-3 days)

Objectives: Part 1: Students will: be able to race in a 100-meter dash in small groups; be able to track and calculate their classmates’ times to the nearest thousandth (if possible); record all classmates’ names and times accurately on a given table; be able to order decimal numbers in order from least to greatest and greatest to least; be able to justify who won the race.

Materials: Stop watches, base-ten blocks, number lines, hundredths grids, place value charts, journals, table, glue sticks, and scissors.

Procedures:

1. Review comparing decimal numbers by using airplane data.
2. Introduce ordering numbers by having students order numbers from least to greatest and greatest to least from within the building such as ages, grades, homeroom numbers, etc. Record and label the orders.
3. Discuss what tools can be used to order numbers if they get stuck. Model the examples.
4. Use and order four numbers from the airplane data using the tools students suggested. Discuss the different ways the decimal numbers were ordered and why they were ordered that way.
5. Explain to students that they will practice ordering decimal numbers in small groups today, and they will get their data from relay races. (Wait for the shouting or pouting to end.)
6. Students will gather journals to cut and paste tables.
7. Students will count off in the number of groups I want there to be based on the number of students I want to be in each group. I would like four students in each group if possible.
8. Students will travel to the gymnasium or outdoor location for the relay races with journals and writing utensils.
9. I will explain directions to students in the classroom as well as review them in the actual location. Each student gets one time to run. All students must record the data accurately. We will cheer our classmates on. We will be good sports. We will sit when it is not our turn to race. We will give as close to accurate race times. We will race fairly. Students may generate some guidelines as well.
10. Students will race against each other in their groups. Classmates will cheer them on, record their times, and calculate their times. It is my goal to have multiple students’ record the times, so we can compare the differences in the numbers they get. However, we will agree on the numbers we will record so that our data is consistent.
11. Once all students have completed the race, we will return to our classroom.
12. Students will work in their racing groups to order their times in order from least to greatest and greatest to least. They will record the times to the nearest thousandth of a second, if possible, in their journals. (This information will be necessary for part 2.)
13. Students will write who came in first place and provide reasoning.
14. Students will share with the class in small groups.
15. Discussion on what students noticed about the numbers. Why is the largest number the winner in the airplane activity, but the smallest number is the winner in the racing activity?
    1. Optional: Order the entire class list from who finished the race first to who finished last.

Closure: Exit slip - Students will explain why the smallest number in their group is determined the winner of the race.

Objectives: Part 2: Students will choose a classmate and use their number to compare similar adjacent digits by stating how many times larger or smaller the same digit is in a different place. Students will show how to compare the value of this same number using a comparison symbol to show which number is greater. Students will also need to state of these two numbers, which friend won the race. Students will use the Clock Buddy Strategy to determine partners.

Materials: Journals, Clock Buddy Template, I will create a template to help students organize information in journals, glue sticks, scissors, place value charts, number lines, base-ten blocks, hundredths grids, and colored pencils or crayons.

Procedures:

1. Distribute Clock Buddy Templates. One for each student. Each student will need to write their name and date at the top of the paper.
2. Students will stand and find a clock buddy for 12 o’clock and then return to their seats. This is to ensure each person has a buddy. The same process will occur until each all 4 time slots are filled.
3. Once all slots are filled, put clocks to the side. They will be used later in the lesson.
4. Students will review what it means to recognize that in a multi-digit number, a digit in one place represents 10 times as much as it represents in the place to its right and 1/10 of what it represents in the place to its left. Sample 1: Explain the relationship between the two 5's in the number 355.921. (Students should be able to discuss and explain the 5 in the ones place is 1/10 the size of the 5 in the tens place OR the 5 in the tens place is ten times the size of the 5 in the ones place. It would take ten groups of 5 to equal the among that is in the tens place OR the 5 in the tens place has a value of 50 and for it to be equal to 5, it would need to divide into 10 equal groups.) Sample 2: I will use numbers from the races.
5. Ask students to refer to their Clock Buddies, choose a time, and students will proceed to begin comparing similar digits in their numbers. Students will also write an inequality to compare their race times, and who won the race based on their time. Each partnership will last about 10-12 minutes.
6. This will continue for four rounds. Students should have four examples of each intended target of this lesson.
7. 3-5 students will share out their comparisons.

Closing: Each student will complete an exit slip independently. I will choose two numbers for students to show their understanding of the intended learning target.

Objectives: Part 3: Project Based Learning Activity- Students will: use their personal racing data to record their individual time in word form, standard form, and the two expanded forms (as decimals and fractions); compare similar adjacent digits by stating how many times larger or smaller the same digit is in a different place in a different number; show how to compare the value of the same numbers using a comparison symbol to show which number is greater;  determine and record which friend won the race and how they know.

Materials: Stop watches, paper, gymnasium or outdoor courtyard, poster paper, base-ten blocks, hundredths grids, place value charts, number lines, markers, glue, or chalk.

Procedures:

1. Students will record their individual time in word form, standard form, and the three expanded forms (as decimals and fractions) independently. I will circulate around the room to clarify or probe students to think, I will also record who needed support and with what.
2. Once all students are complete. I will introduce the Decimal Place Value Poster Project.
   1. Title
   2. Group Member Names
   3. Individual Group Member Data using the four stages of place value. (May be directly written on the poster or written in a provided table and glued to the poster).
   4. Order group members numbers form greatest to least.
   5. Order group members numbers form least to greatest.
   6. Write 2-4 inequalities comparing the racing times.
   7. Write a sentence explaining who won the race and how the group knows.
   8. Poster is neat and organized.
   9. Class presentation.
3. A rubric will be used to evaluate the students.

Closure: Students will present their project to the class. (I anticipate this taking a few class periods).