Problem Sets
In addition to the abstract content of permutations, combinations, binomial and multinomial coefficients, a goal of this unit is to have my students quantify situations that they encounter on a frequent basis. Classic textbook problems involving permutations and combinations utilize sets of objects such as a standard 52-deck of playing cards, 6-sided die, 2-sided coins, and telephone numbers. Though these objects may seem mundane to most, I had students struggle significantly with the topics in this unit because they were unfamiliar with a deck of cards. Throughout this unit, I will make sure to include more traditional problems, because they do appear on standardized tests, but first I will give my students a chance to practice the concepts and skills within familiar contexts that are part of their daily life.
Menu Options
My students love food. The following are sample questions that are modeled from different restaurant menus from around our local neighborhood.
Scenario #1
Ricky goes to Denny’s and wants to order a Grand Slam for breakfast. For the Grand Slam, he can select any four items from a list of 13 items. How many different breakfasts can Ricky order?
Extension: Ricky can upgrade his Grand Slam to a Super Grand Slam by adding a fifth item to his meal. How many different 5-item Super Grand Slams can Ricky order?
Scenario #2
Josephine is ordering a poke bowl. She wants a regular bowl and must choose a base of white or brown rice, one of six different choices of fish/protein, two of 8 different sauces, and 5 of 12 different toppings. How many different bowls are possible?
Extension: A large bowl allows two scoops of fish/protein and 7 different toppings. How many more large bowl combinations are possible compared to regular bowls?
Scenario #3
Vinh is ordering pizza for School Site Council. He can choose either a thin, hand-tossed or pan pizza crust, with one of five different sauces. Also, Vinh must specify if he wants a normal amount of sauce, extra sauce, or light sauce. A pizza can be topped off with a choice of 8 different meats and 16 different non-meat toppings. Since his coupon only allows for 3 toppings, how many different 3-topping pizzas are possible? Vinh must consider that some people at the meeting are vegetarians. How many 3-toppping, non-meat pizzas can he order? Vinh also decides to have some variety and wants to make some pizzas with 1 meat and 2 non-meat toppings. How many of these pizzas are possible? Are there the same number of possible pizzas with 2-meat toppings and 1 non-meat topping as there are pizzas with 1 meat and 2 non-meat toppings?
Scenario #4
At a Cracker Barrel restaurant, each of the 6 dinner entrees comes with the customer’s choice of three sides. There are 23 different sides available. How many dinner combinations are possible?
Extension: If you had one dinner per day at Cracker Barrel, could you eat a different meal every day for a year? For 2 years? For 3 years?
Scenario #5
Jason likes to drink way too much milk tea. His favorite milk tea spot offers 8 different types of tea. After selecting a tea, he must choose between a small or large size, 5 different sugar levels, 5 different levels of ice. How many different tea drinks are possible?
Extension Questions: Jason realizes that he forgot to add toppings. There 9 toppings available and he can choose to add up to two toppings to any drink. How many drinks are possible?
Fun and Games
This set of problems involves toys, board games, and card games.
Game #1
Consider a standard 3x3 Rubik’s cube. There are 6 center pieces that are fixed. There are 8 corner pieces and 12 edge pieces. Suppose that corner pieces can be interchanged with each other and the edge pieces interchanged with each other. Find the number of different patterns that can be produced assuming all permutations of corners and edges are possible.
Extension: How many permutations of face cubes are possible on 4x4 Rubik’s cube? Note that for the 4x4, there are no center cubes, and no fixed relation between a given face and a color. If you could display 1 permutation per second, how long would it take to cycle through all the permutations for a 3x3? A 4x4? If a computer can go through 350 billion permutations per second, how long would it take to cycle through all the permutations for a 3x3? A 4x4?
Game #2
A Boggle board has 16 slots. There are 16 6-sided dice with different letters of the alphabet printed on the sides. How many Boggle board permutations are there?
Game #3
In Mastermind, one player creates a 4 color code (a sequence of 4 colors) while the other player tries to guess the code. If there are 6 different colors and, colors can be repeated, how many different codes can be made?
Game #4
To play the card game 13, a standard deck of 52 cards is shuffled and 4 hands of 13 cards are dealt. How many different 13-card hands are possible?
Game #5
The badminton team has 7 girls singles athletes. The top three make it to varsity. How many different varsity lineups are possible?
Culminating Project - Password Combinations
With continual developments in technology, we interact and count with numbers of ever increasing size. There is a need to enumerate and comprehend numbers at increasing degrees of magnitude. A decade ago, the kilobyte and megabyte were the units to store our computer data. Today, we utilize gigabytes and terabytes, as standards for personal data storage.
Passwords are a context where it is easy to count and compare the total number of possible ways when the length is relatively small and as restrictions are introduced or relaxed. As the length increases, and the number of restrictions and conditions change, the number of potential passwords increases rapidly.
As a culminating project, students will evaluate the effectiveness of our district’s password policies. Based on their computations, they will make recommendations for or against policy changes.
To start, students will compare passwords with a length of four.
Four digit pin numbers are often used for bank ATM cards and cell phone locks. How many possible 4-digit codes are there?
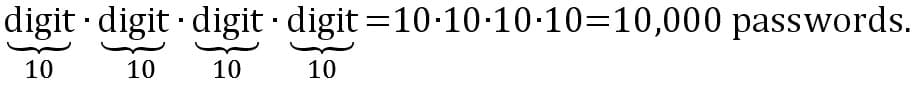
If you were to use four letters of the alphabet, how many 4-letter passwords are there?

Varying the numbers of letters and digits allowed also affects the number of passwords. If we only had one digit followed by three letters, we have:

Taking 2 digits and then 2 letters gives:
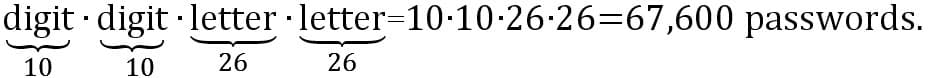
I would have students consider whether the placement of the 2 digits and 2 letters in a password changes the number of passwords. Also, I would have them look at 1 digit and 3 letters where the digit can change position in the password sequence.
If you could use an alphanumeric code, where the digits 0 to 9 and the letters A-Z are included, how many 4-character passwords are there?

For many students, the amount of over 1.6 million passwords seems very secure, but a computer can run through all possible combinations nearly instantaneously for only 4 characters. A standard computer can guess approximately 350 billion passwords a second. Using that knowledge, students are posed the following scenario: Our district requires students to create passwords that are at least 8 characters, where there is at least one upper case letter, at least one lower case letter, at least one digit, and at least one of six special characters. Are these requirements necessary or should they be changed? If you believe that the policy is sufficient, explain why. If you believe there should be changes, explain why. How many alphanumeric 8 letter codes are there? Assuming that a computer can check 350 billion passwords per second, how many seconds would it take for the computer to check all passwords?
Students would be permitted to work in groups of up to three and would submit their responses in a format of their choice, which may include but not limited to a written explanation, PowerPoint presentation, poster, or video. Their final project will also be examined by a non-math teacher, which requires the students to make sure their arguments are clear and understandable to a broader audience.

Comments: