Learning Goals
The objectives of this unit revolve around raising the skill level or ability of my students in three key processes: counting, measuring, and critical thinking. The vehicle for presenting this opportunity for growth is the polyomino. I should talk a bit about polyominoes to aid in the understanding of my goals.
Polyominoes
Polyominoes are shapes that are created by assembling congruent squares. The rules of assembly are:
- Two squares that touch do so either at a corner of each, or along a full edge of each.
- The figure is connected, in the sense that one can move from any square to any other square by passing through middles of edges (i.e., not passing through corners).
(See Figure 1). These shapes can be small or large, depending on the number of squares that are connected together. The flexibility offered by the polyomino as a tool in my lesson means that these shapes can be easily differentiated to meet the needs of students. For example, the bulk of the class may find it challenging but accessible to work with tetrominoes (polyominoes made of four squares). The use of trominos (made of three squares) would perhaps be more accessible for struggling students. To meet the needs of advanced students or even as an extension activity for students who have successfully mastered the tetromino, the pentomino or even hexomino (shapes of 5 or 6 connected squares respectively) could be a good option.
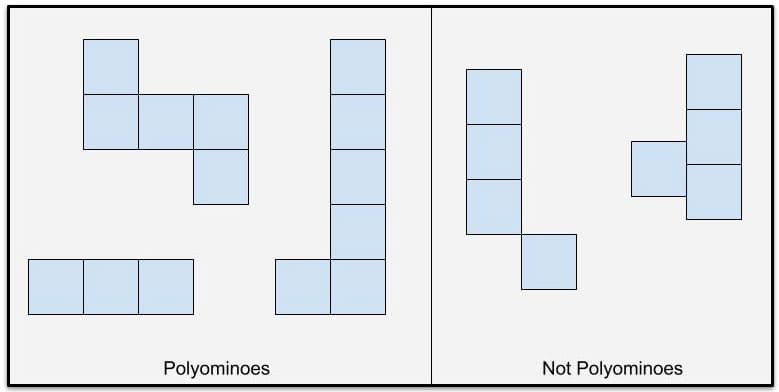
Figure 1: The left box shows polyominoes made of congruent squares sharing a common edge. In the right box are examples of non-polyominoes. Each violates one of the conditions i) or ii).
Counting
In kindergarten we count. Mostly this activity takes the form of counting physical objects (fluffy balls, cubes, plastic bears, seashells, and the like.) Counting in this form is necessary, as the act allows children to develop strategies to aid in the work; for example organizing all the bears in a straight line before beginning the count is helpful. I have come to realize that there could be another way to count that offers an added benefit. In this unit I will be asking students to count various attributes, such as the number of squares (the area), the number of exposed edges (the perimeter), the number of straight sides or the number of vertices, of polyominoes (see Figure 2). I asked myself, “Will counting the straight sides or vertices of a polyomino allow the student to practice counting?” The answer is yes. “Will the counting of straight sides or vertices allow the student to develop strategies to assure that they are counting in an organized manner?” Yes, again. But, I also recognize that something else is happening. The students will be reinforcing their knowledge of shape. Specifically, they will be reinforcing their understanding of the vocabulary every time they count the corresponding attributes. So instead of reinforcing our concept of plastic bears, we are deeply interacting with an attribute of geometric shapes. As a bonus, since my students have been mostly counting physical objects, this activity of counting attributes will not feel like more of the same. It will present the act of counting as something new and different. Reinforcing geometric vocabulary and concepts plus minimizing the boredom of counting manipulatives over and over, equals a win for both educator and student.
The counting of straight sides and vertices offers an additional opportunity for learning. Polygons are closed shapes. Polygons are constructed of some number of line segments. These line segments share endpoints with the adjacent straight sides of the polygon. Because of the sharing of endpoints and the closed nature of polygons, the number of straight sides will always be equal to the number of vertices. As we record our data regarding these attributes, I will guide my students to this discovery. It will show that counting can lead to larger discoveries. This will aid my students later in the year when we are explicitly observing the attributes of shapes. Generally speaking, my students have an easy time recalling the number of straight sides to a shape, but they sometimes find it more challenging to remember the number of vertices. Knowing that the number of straight sides and vertices are always equal in polygons will help them in our geometry unit.

Figure 2: On the left the vertices are counted, note even interior vertices are counted. On the right, counting the total straight sides.
Measurement
We have a way of practicing measurement in kindergarten. We measure in non-standard units. Usually we will measure a physical object (like our foot, or a pencil lengthwise) with connecting cubes, or popsicle sticks, or paper clips. This sort of measurement makes sense and is certainly a valuable experience. After all, once standardized units are introduced in the later grades, kids still measure something with a physical tool (ruler, yardstick, etc.). However, in this unit my students will be measuring polyominoes. We will not be measuring length (a typical activity for grade K.) We will be exploring perimeter and area. HOLD THE PHONE! Those are definitely not mentioned in the CCSS for K. In the CCSS, measuring largely deals with examining the length or weight of a given object. Further it is required that kids compare similar attributes of two objects. Thanks to the ‘connected square’, grid-like appearance of polyominoes, it will be super easy for students to ‘see’ the perimeter by counting the edges of the squares around the outside of the shape. Area is even easier to count, as they just count up the total number of squares in their polyomino (see Figure 3). This counting of congruent squares can even lead to an observation that when measuring we are counting objects (units) of equivalent size (e.g., paper clips, connecting cubes, inches, or miles, depending on the context).
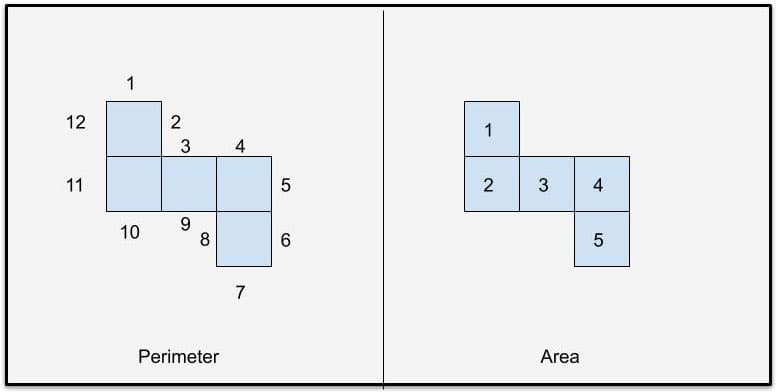
Figure 3: The left box shows the measurement of perimeter of this pentomino. To the right is the measure of area for a congruent shape.
Since the units we are measuring are not paper clips, but squares, kindergarten kids will be measuring area in, wait for it… square units. Think about that, would it be helpful for a student to enter third or fourth grade with a recollection of measuring area in square units before? I think this is a wonderful bit of knowledge that could serve these students well. Imagine, a group of children who when confronted with a concept like square units can draw upon an image of a shape constructed of congruent squares. That would boost math confidence. That would be an example of engaging with Math Practice 4 (math models) from the Common Core. “This shape is blue and that shape is red” is a typical kindergarten response to a discussion of attributes. They are right and I’d be happy with the answer, but imagine hearing this: “Those two shapes are alike because they both have an area of 4 square units”. These polyominoes can also afford my students the opportunity to make discoveries about the concepts of perimeter and area. For example, polyominoes of equal area can have differing perimeters (see Figure 4). Or, by changing the arrangement of our connected squares we can maintain area and can either raise or lower perimeter. This idea will highlight the fact that area and perimeter are two separate and independent concepts. I am excited at the prospect of leading the math talk about that.
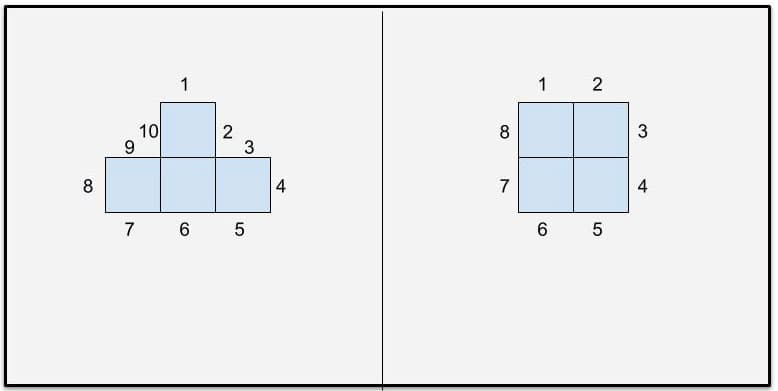
Figure 4: Both of the above tetrominoes have an area of 4 square units. The perimeters of these shapes differ.
Measuring polyominoes will increase the level of rigor in my class discussions of mathematics. The deeper the math chatter is, the greater the sense of math concepts that my students will develop.
Critical Thinking
Students need opportunities to think. This seems obvious, but too often what is required of primary students involves little thought. Unimaginative tasks yield unimaginative solutions and result in unimaginative students. A worksheet problem that asks a student to draw 4 flowers requires little consideration, even from our littlest scholars. This unit was designed to challenge young scholars. Through the activities detailed below students will be practicing skills such as those mentioned above, but they must also make models, make choices, and justify those choices using data gathered by counting and measuring and studying attributes of geometric shapes. They will have to sort shapes based on their attributes to best match a set of requirements. Put simply, they will be required to think. They will be supported throughout the process and they will succeed. They will be engaged in rigorous and relevant lessons as they create polyominoes, and address multiple CCSS in a thoughtful and purposeful way.
Other Items to Consider
Spatial Awareness
In a case study by Moss, Hawes, Naqvi, and Caswell we read: “Increased efforts are needed to meet the demand for high quality mathematics in early years classrooms. Despite the foundational role of geometry and spatial reasoning for later mathematics success, the strand receives inadequate instructional time and is limited to concepts of static geometry.”2 I find this assertion alarming, as should all practitioners of early childhood education. Spatial reasoning/awareness is important and yet lacking in most classrooms. To me, this is unacceptable. Spatial reasoning is one of the 9 identified types of intelligence. I have witnessed that some of the least traditionally academically gifted students excel with spatial reasoning. Activities that require them to manipulate shapes in space are their opportunity to shine. There is something powerful about watching a child who struggles demonstrate high competence at a task. The opportunity for students who struggle elsewhere to share their expertise with a peer is confidence building. The tasks in this unit will directly respond to the charges above. Students working through these activities will move beyond static geometry. They will be manipulating shapes and looking closely at their attributes and parts.
Interconnectivity of the Math Strands
A goal of mathematics education is to create numerate citizens. The New Zealand Ministry of Education has stated; “Numerate students are able to apply their number understanding to a range of content, from the other strands in mathematics.”3 I have found that sequencing and pacing of the curriculum tends to isolate geometry, and to a lesser extent measuring and data, from the rest of the math strands. As previously stated, my students don’t even consider geometry work as part of math. This is a missed opportunity to strengthen the impact of our unit. If we are able to make clearer and deeper connections between the strands in our lessons, then this unit will be addressing standards from multiple strands. This connectivity should aid in retention of information and the recall of all concepts involved. Moreover, connectivity does not necessarily relate to only grade level content. Linda Gojak, the president of the National Council of Teachers of Mathematics stated; “it is important to think about the connections among concepts within the grade level or courses that we teach, it is also important to reflect on the connections across grade levels.”4 The memories students will have of these lessons will resurface a few years down the road and connect our explorations and takeaways from polyominoes into a solid basis for their new lessons on area and perimeter.
New Connections and Innovations, Same Standards: A Brief Overview of the Unit
Activity One: Meeting Polyominoes
I will present the students with this challenge statement; “Given four square tiles, find and record as many different shapes (tetrominoes) as you can.” I will then introduce conditions i) and ii) for the creation of these shapes.
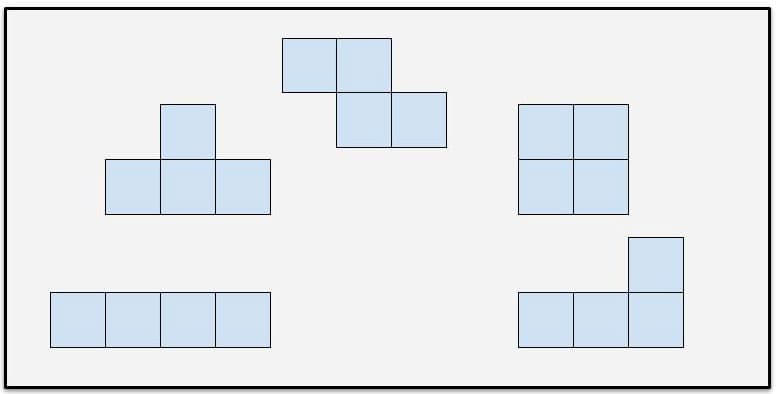
Figure 5: These are all the tetrominoes.
This activity will have many positive outcomes. One outcome is that it will address the CCSS, K.G.B.4, which basically requires students to describe similarities and differences between shapes by examining their parts and attributes. Typically, kindergarten interacts with this standard by comparing regular polygons, such as a triangle and a square. They then compare and contrast the two. They may note that both shapes have corners or that there are differences in the numbers of sides. Examining the tetrominoes will require a more critical eye for details. Further, discussing the similarities and differences between two of these polyominoes will demand a more rigorous level of explanation. Instead of ‘they both have straight sides”, the observation could be more like “they both have three squares connected in a row.” This deeper level of discussion would be indicative of a deeper level of mathematical thinking. A second benefit of having students work through this activity is that they will be developing ‘math endurance’ and perseverance during math studies. Finding new and unique polyominoes can be challenging, though due to the hands-on nature of these explorations, still engaging and even fun (see Figure 5) Working through mathematical challenges and struggling through mathematical processes is the only way to truly strengthen the CCSS Math Practice 1, which is all about persevering through tasks. Finally, during this lesson, I will be introducing or reinforcing vocabulary. Common kindergarten words that will be reviewed and reinforced through this activity are attribute, similarities, and differences. These three terms are highly important as they cut across the content areas of our curriculum. Additionally, this will give me the opportunity to expose my students to the terms rotation, reflection, and translation. These really aren’t kindergarten terminology, but I know my young students can manage them and my class is almost always super excited to receive “secret older kid knowledge”, that I of course tell them they are not even allowed to know. The terms rotation, reflection, and translation will naturally enter our conversations as we determine whether similar shapes (say a left facing and a right facing L shaped tetromino) are indeed different shapes. The students will find that we can discover many similar shapes by simply manipulating our tetrominoes.
Activity Two: Counting
Once introduced and familiar with the tetrominoes, I will challenge my students to “examine our new shapes and to then count and record the numbers of vertices and straight sides of each tetromino.” This is a central task of my unit; COUNTING. As indicated earlier, my students need to be counting everyday. The counting also has to look and feel different to stave off lack of engagement. I honestly believe that my students will not even realize they are busily counting. To them, they will just be exploring attributes off ‘their’ shapes. (Allowing the students struggle to find these shapes in activity one gives them a sense of ownership for these polyominoes.) But in my evil genius mind, I’ve got them counting a whole bunch: “Mwuhaha”. Point in fact; as the school year progresses, and I continue to involve my students in counting, I can circle back to this activity by introducing pentominoes. Adding a fifth square tile will increase the level of challenge, and of course the amount of vertices and straight sides possible. Working with the pentominoes will feel familiar enough that this activity could easily be introduced into math workshop. The activity will also offer enough new challenge, that my students should not find it boring.
There are multiple positive outcomes of Activity Two. First and foremost, we will be addressing several required standards of the CCSS. As my students record their counts they will be practicing writing numerals. K.CC.A.3 requires that students can represent a number of objects (or in this case attributes of tetrominoes) with the written numeral. The skills of standard K.CC.B.4 are awakened anytime counting occurs correctly and highlights the relationship between quantities and numbers. My class will also be answering those “how many” questions (as in how many vertices are in this shape) as prescribed by CCSS K.CC.B.5. This lesson also focuses student attention on standard K.G.B.4; a geometry standard that focuses on exploring similarities and differences between shapes with a focus on the attributes and parts of those shapes. This activity allows me to link two different math strands together, connecting geometry to counting and cardinality. The lesson provides an opportunity to explore the relationship between vertices and sides of polygons. The number of sides will always equal the number of vertices. This is because a vertex acts as an endpoint of a straight side. Each adjoining side is connected at a shared endpoint. So 4 sides equals 4 vertices. This relationship could be a useful bit of knowledge to aid the students in remembering the attributes of regular polygons. In my experience, young students more easily remember the number of sides than that of vertices. Knowing they are always equal, will aid in describing the attributes of a given polygon.
Activity Three: Measurement
Activity Three presents a similar but different challenge to my students than the last activity. They will explore the tetromino shapes and then measure and record the perimeter and area of each shape. I anticipate that my students will have a challenging time differentiating perimeter and the number of straight sides. This confusion does open the door for me to point out a major difference between counting and measuring. It will be easy to show them that when counting straight sides, the lengths of those sides may (though not always) vary. When measuring the perimeter we are not counting sides, but the number of the edges of the squares that make up the shape. Unlike the lengths of the sides of a polygon that may be different, all of the edges of our squares have the same length. Measuring requires units of the same size, while length is ignored in the concept of “side”(see Figure 6). It will often turn out that shapes with quite different numbers of straight sides will have the same perimeter!
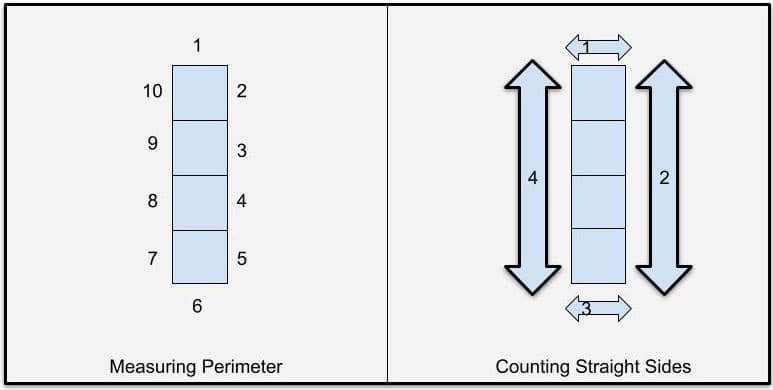
Figure 6: The differences between measuring perimeter and counting straight sides is highlighted. The difference will require explicit teaching.
As a result of this activity the class will be engaging with several Common Core standards. Firstly, standard K.MD.A.1 will be addressed. This unit has students describing measurable attributes of shapes (area, perimeter). They will also be revisiting the same Counting and Cardinality standards as the prior lesson. Much as the last lesson drew a connection between counting and cardinality and geometry, this lesson will tie the counting and cardinality and measuring and data strands together, as well as connect them both to geometry through geometric measurement. Connected strands make for easier recall and deeper understanding. As with the other activities in this unit, vocabulary will also be introduced or revisited. Terms for the students will now include perimeter, area, and measurement.
Activity Four: Critical Thinking
This final activity will begin with a story, which I include now. “I have a fence in my backyard. I also have three dogs. Bean loves walking the fence. She always looks for squirrels and wants to change directions a lot. Dory loves walking the fence too. But she wants a long stretch of fence to race along. Izzy also loves walking the fence. She would like a fence that gives her a very long walk.” With this story in mind, my students will pretend that my backyard fence is in the shape of one of our tetrominoes. They will be challenged to match a fence (shape) up to each dog that would satisfy that dog’s desires. I will further insist that students justify their pairings of fences to dogs. This lesson will grant access to several CCSS for my students. Tetrominoes will be sorted into different categories. The specific categories, while based on the dogs from the stories, will in truth be based on attributes of the shapes. Bean’s fences will have the most vertices possible. Dory’s fence will have the sides of the greatest possible length (it will be a 1 by 4 rectangle, in the case of tetrominoes.) Izzy’s fences will have the greatest perimeter. This classification of objects is related to standard K.MD.B.3. While my students are comparing objects by considering their attributes, they are also working to master standard K.MD.A.2. A major reason for this activity is to engage students in a critical thinking exercise. They are required to consider multiple shapes and determine which of the shapes has more or less of a given attribute. They must then justify their selection by explaining why it would be the best choice for Bean, Dory, or Izzy. This type of thinking will engage the student with Math Practice 3: constructing viable arguments. This final activity will also reinforce much of the vocabulary that has been in use throughout the unit. It is worth noting, that while Dory will always find one perfect shape for her, Izzy and Bean may find multiple shapes that will satisfy their wishes. There will be an opportunity for an interesting math discussion if teams of students find different (though both viable) solutions for Izzy or Bean. Questions surrounding different shapes with the same perimeter or number of vertices could provoke a valuable conversation. An interesting bonus task could be to have the students identify the only shape that would not match any of the dogs’ preferences (it’s the square-shaped tetromino). Another possible adaptation would be to change the names of the dogs (Bean, Dory, and Izzy are my actual pets and I refer to them frequently during the school year so my students have a connection to them). Without this connection it may best to change their names to better scaffold the activity. Bean could become Victoria as she loves Vertices. Izzy could become Percy, to match Perimeter. Dory could become Larry, for Long distance.
Summary of Benefits
This level of rigor is rare in kindergarten. In the typical K class the students have many opportunities to talk math and solve challenges, but the segmented appearance and hands-on nature of the polyominoes makes incredibly high-level math thinking accessible for even the youngest of students. The students will be determining perimeter and area, using standard measurement like square units, and focusing deeply on the geometric attributes of shapes. These three too often disparate strands of our mathematics curriculum are twined together making a strong rope of knowledge leading the students beyond the typical. The fact that my students will be exposed to content from upper grades in a manner that will allow them to both understand and successfully complete activities will give them a leg up when the content is revisited in later years. Meanwhile, the subtext of this unit is that while all this heavy lifting is being undertaken, the students are also practicing multiple critical kindergarten standards from multiple strands of the CCSS.
Possible Extension Activities
As stated earlier, I am always looking for ways to engage my students in things that will allow them to practice basic skills in exciting ways. This unit can be easily differentiated or extended as time and student interest allow. It is easily scaled up by using polyominoes with more than four tiles. Introduce a 5th tile and the polyomino’s area goes to 5 – you get a pentomino. While there are only 5 distinct tetrominoes, there will be 12 distinct, pentomino arrangements. Adding a sixth tile and creating hexominos raises the total number of distinct shapes all the way to 35.
Another potential way to extend the unit and raise the level of challenge is to move away from polyominoes altogether and explore polyiamonds. Polyiamonds are very similar to polyominoes Polyiamonds are made not with square tiles but by connecting congruent equilateral triangles by at least 1 common edge. This substitution would keep the basic lessons the same but is would give it a new appearance and feel to the students. In this variation, I would move my discussions of area back to nonstandard units by measuring the area in triangles. Another substitution for the square tiles would be hexagonal pattern blocks. Connecting these congruent shapes would have the students creating polyhexes.5

Comments: