Content
What is a fraction? Why do we have to teach fractions? Where do we use fractions in the real world? The most common fraction used in everyday language is half or one-half. For example, you often hear people say just get half, get half of it, share, given them half and so on. When do people say half are they really thinking about the concepts of fractions? Are they really thinking of parts of whole or parts of a collections?
Surprisingly, fractions can be found and utilized in many places. Some of the most familiar places include recipes, and various forms of measurements (liquids and lengths). Most of the time a fraction is defined as some number of equal parts of a whole or parts of a collection.
A common or simple fraction is often shown with a numerator displayed above a line or slash, and a non-zero denominator shown below or after the line. The numerators and denominators are natural numbers. In mathematics, natural numbers are the 1, 2, 3, etc.… sometimes referred to as whole numbers in elementary school,6 and known as counting numbers to primary students. Other fractions that use numerators and denominators include compound fractions (complex fractions), and mixed numerals. Compound fractions, also known as complex fractions, describe a fraction in which a numerator or denominator, or both, contain fractions. A mixed numeral, also known as a mixed number, is a whole number, and a proper fraction represented together. It is understood to represent the sum of the whole number and the fraction. (See Table 1 for examples.)
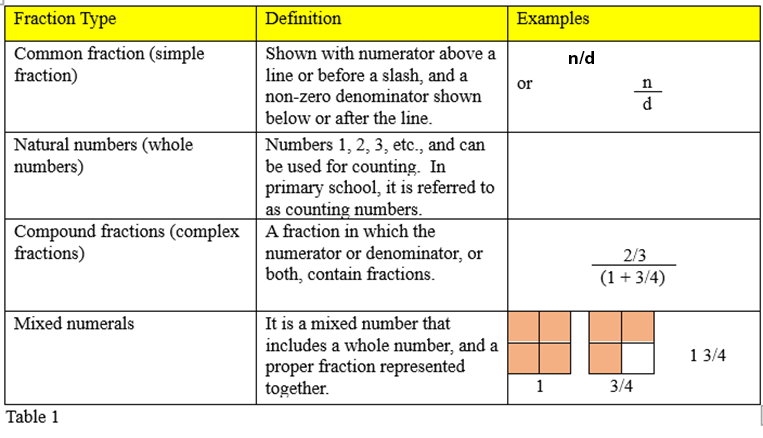
Table 1 - Fraction Types
The numerator represents a number of equal parts left, and the denominator tells how many equal parts to divide the unit into which represents how many total parts make up the whole. The denominator cannot be zero because you must always have at least one part to make anything (other than zero). Zero parts cannot make a whole. For example, suppose you have ¾ of a pie. The three is the numerator that represents the number of parts present, while the four represents the parts that make-up the whole. The four tells how many (equal!) parts the pie is cut into, and the three says to take three of those parts. A common fraction may also be thought of as a quotient: ¾ can represent three divided into four equal parts. This equivalence can be illustrated nicely with the number line. In arithmetic, a common fraction is a numerical representation of a rational number that is defined as a quotient, in which the numerator is divided by the denominator. Fractions can also be represented as decimals, percentages, or negative exponents. For example, ¼ is the same as 0.25, 2-2, or 25%. Fractions can also be represented by ratios and division. Again, ¼ can represent a ratio of 1:4, and the division of one divided by four.7
There are so many possibilities and representations of fractions. As teachers, we try to teach fractions in a rational “sequential” order, but students need to realize that decimals, fractions, percentage, division, and ratios are all part of one system. Fraction is one of the mathematical concepts that is hard to convey to students, especially since it is no longer dealing with whole numbers, but parts. How will I prevent fractions from confusing my students? One idea that will be used in this unit is to introduce fractions in terms of distance.
A third-grade standard according to the Arizona Department of education states that: students will be able to partition shapes into parts with equal areas and express the area of each part as a unit fraction of the whole. Beyond Textbook, our current curriculum framework, states that according to the performance level indicators for proficient students, students should be able to partition shapes into b parts with equal areas, and students should express the area of each part as a unit fraction 1/b of the whole. Expectations for third grade are limited to fractions with denominators b = 2,3,4,6,8. The learning target for high proficiency students is that they can partition shapes into parts with equal areas and express the area as a unit fraction of the whole to answer questions presented in context. The relevant ideas for this unit are: shapes can be partitioned into equal parts and the parts can be represented as a fraction; one shape can be partitioned equally in diverse ways while still representing the same fraction. The shapes we should work with include quadrilaterals (rhombus rectangle, squares, isosceles trapezoids) isosceles triangles, regular hexagons, and circles.8
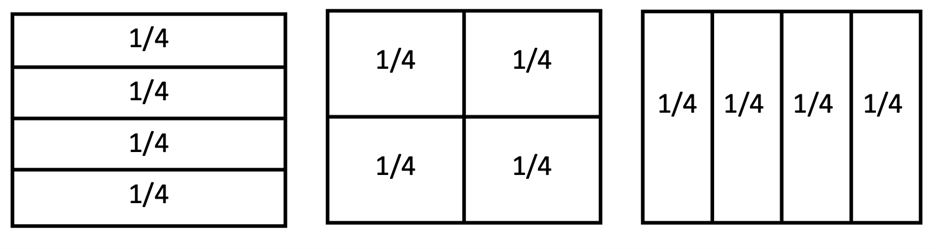
Figure 1 – Four Different ways to partition fourths.
The preferred model to use for fractions is to partition a shape into the division of equal parts. In this model students will partition a rectangle into fourths and all will represent the same fraction three diverse ways. The parts will have equal areas, and students should express the area as a unit fraction of the whole. Furthermore, the students will be required to recognize the fraction of the area of a shape that is represented by a part, identify the shapes that are divided into equal areas, shade a fraction of a shape, match given partitions with the correct fraction, and to construct a complete shape given only one of the partitioned areas of the whole shape.
Teachers within a grade level and subject then collaborate to “unwrap” the standards to determine essential ideas, key vocabulary, student-friendly language, essential questions, and performance tasks that prove mastery. "The documents produced in this process form the foundation of the core subject curriculums at each grade level and establish district-wide expectations for what teachers should teach and what students should learn and be able to do in relation to a specific standard.9
Beyond Textbook reviewed state content standards to identify core sets of essential standards that established what students must learn in each content area at each grade level.10 These are the standards that will provide students with what they need to learn by state assessment time. Additional standards are not as important as what Beyond Textbook deems as essential standards. Although the standard that states that students will “understand a fraction as a point on a number line; represent fractions on a number line diagram; and understand a fraction 1/b as a special type of a fraction can be referred to as a unit fraction (e.g. ½, ¼)”, is not an essential standard according to Beyond Textbook, I believe that students still need to learn to use number lines to learn fractions. Utilizing number lines “help us understand arithmetic in terms of geometry11.” So rather than working with symbols, number lines help us establish a more unified picture of what arithmetic is about and help students make more sense of it. However, before we begin, I should discuss what is a number line and how it would look.

Figure 2 – Standard Number Line
A standard number line looks like this, a line with ticks which have unit intervals between them, which are equal to a unit length like a ruler. The important thing about a ruler is that it measures length or distance. Length is the size of the line, or any long and thin linear object like a rod or a tape.
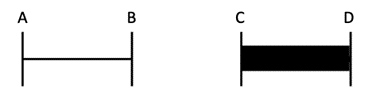
Figure 3 Thickness of a line does not determine length.
Despite the thickness of an object or a line, they can be measured to the same length. A line could be one inch, and a thin strip could also measure an inch unit interval that has two points that are the same distance apart. Distance refers to the length of the line between two points. The distance between A and B is the same unit distance and the same unit distance between C and D. In general, the length of a straight line is the distance between its endpoints, and vice versa.12 In order to measure length, a unit of length needs to be chosen, such as centimeter, foot, meter, inch, or any unit that measures length. Length, units of measurements, distance, straight lines, and endpoints are all involved in constructing a number line.
Creating a Number Line
As adults, we have seen and have constructed number lines, but a child who has never seen or has any experience with number lines will need help with the process of constructing a number line. How do you begin and how do you explain it to a third-grade student?
To begin the construction of a number line, you start with an unmarked straight line.

Figure 4 – An unmarked straight line.
The next step is to choose a point of origin or a zero point. Since I will only be working with positive numbers, I will place the zero point on the left side, but not placed as an endpoint. Students need to understand that a number line is endless in both directions.

Figure 5 – Choose a point of origin on a number line.
Next, you choose a point to be one:

Figure 6 – Establish unit length of 1.
The unit length is established: on the number line, the unit length is length of the interval between 0 and 1.13 The interval between 0 and 1 establishes the position of every number on the number line. The number labeling some other point tells you about the distance between that point and the origin, as a multiple of the unit distance. For example, the point labeled two is at distance of two units from the origin. In the diagram below, you can see that you can fit two intervals of length, one between 0 and 2. The intervals are shown in assorted colors so that it is easy to tell them apart, but they both have length one.

Figure 7 – The unit length between the two intervals is equal length.
As the diagram shows, you can fit three-unit intervals in the space between 0 and 3, and four-unit intervals between in the spaces between 0 and 4, and so on.14
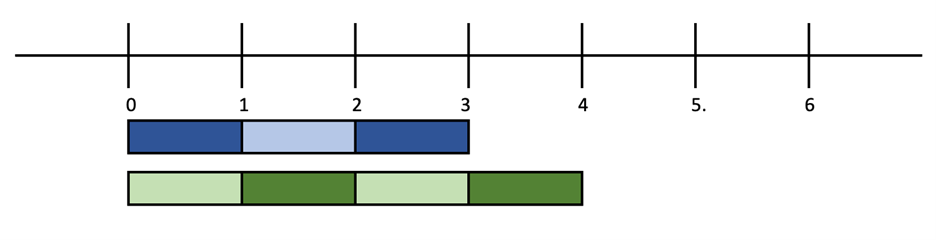
Figure 8 – Unit intervals between 0 and 3, and unit intervals between 0 and 4.
This relationship between unit length and measurements can be applied when we put fractions on a number line. For example, to get an interval of length 1/2, we cut the unit length into two equal pieces, where each one has a length of 1/2:
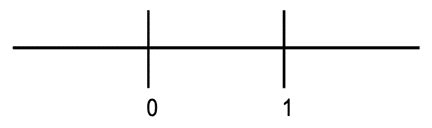
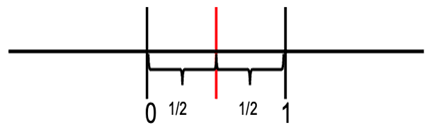
Figure 9 – One interval partitioned into two equal parts to show halves.
According to the rules of relating numbers to distance, 1/2 should label the point at the right end of the interval of length one-half, with its left end at zero.
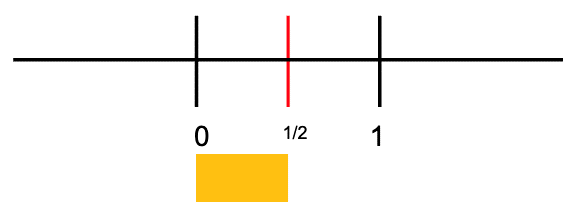
Figure 10 To show an interval of half, the interval begins at 0.
As we continue with one-half, we would put 2/2 at the distance made by two bars of length 1/2, which is the same as one. In arithmetic we learned that 2/2 = 1. As we continue the number line, we would put 3/2 at distance equal to 3 length of 1/2, and 4/2 would go four lengths of 1/2 (which is the same as 2-unit lengths from zero.) This entire process continues, the numbers are arranged in multiples of 1/2, including the whole numbers.15

Figure 11 – The number line is arranged in multiples of halves, including the whole numbers.
Fractions with larger denominators follow the same process. For example, if we want to work with thirds, we divide one unit into three equal parts. The first piece starts at the left end or at zero, and the first piece will end at one-third. To get to the next third (2/3), we take two lengths of 1/3 and put them together, with the first one beginning at 0, and the other end will be at two-thirds. This continues the same pattern, each time we add one-third, it reaches the next third.

Figure 12 – The number line is arranged in multiples of thirds, including the whole numbers.
The number lines showing multiples of 1/2 and the number line showing multiples of 1/3 are like the number line for whole numbers. The only difference is that the number line for one-half is evenly spaced into two pieces for each whole number. The multiples of 1/3 are only 1/3 as far apart as the whole numbers, with three intervals of length 1/3 in every unit interval.16 If the same process is applied to ¼, that would imply that the multiples of 1/4 are only 1/4 as far apart as the whole numbers, with four intervals of length 1/4 in every unit interval.
That means that a whole number would be able to be divided into multiples of any unit fraction. If the denominator is d, the multiples of 1/d are an evenly spaced set of points on the number line, and chopping up each unit interval into d equals smaller intervals. Here is a picture when d = 6.17

Figure 13 – A number line can be divided into multiples of any unit fractions, including sixth.
Comparing Fractions
Now that I have established what a number line is and how to set it up, comes the application of number lines to teach fractions. One main objective is for students to eliminate the confusion and problems of how large a fraction is. Number lines will help students see that as the denominator goes up fraction gets smaller. If students see fractions as measurement of distance, they will be able to distinguish between the intervals of each fraction. In addition, number lines help students compare fractions and find equivalent fractions.
Relative size of fractions causes the most problems when we start comparing fractions. Up to this point in math, I have been teaching students that larger numbers mean “more” when dealing with whole numbers. The students often transfer the knowledge and concepts of whole numbers to fractions. However, fraction is not dealing with whole numbers, but rather a whole unit that is chopped up into smaller unit intervals. For example, we can say that whole number 4 is larger or more than number 2. The students misuse that knowledge of comparing whole numbers to conclude that fourths should be larger than half. The relationship between number of parts and the size, or in the case of number lines, the length of the parts is a hard skill for students to learn. For many students, it is a developmental skill that takes time and repetition to grasp the concept.
For most of us, the rules of comparing fractions or the algorithm for comparing two fractions is finding the common denominator through the process of cross multiplying. This is a great strategy…if you understand fractions, you can get the right answer, but there is no thought that goes into the actual size of the fractions. If children are taught these rules before they have had the opportunity to think about the relative size of various fractions, there is little chance that they will develop any familiarity with or number sense about fraction size.18
So, what do we do? Let us look at some common errors that teachers and students make, especially with fractions that have like denominators. Suppose we compare 1/4 and 3/4. It is common for students to look at only the numerator and decide that 3/4 are larger. They are not wrong, because 3 is larger than 1, and the denominators are the same. But students need to realize that denominators in fractions must also be considered. A visual representation of 1/4 and 3/4 will show students why three-fourths are more than one-fourth.
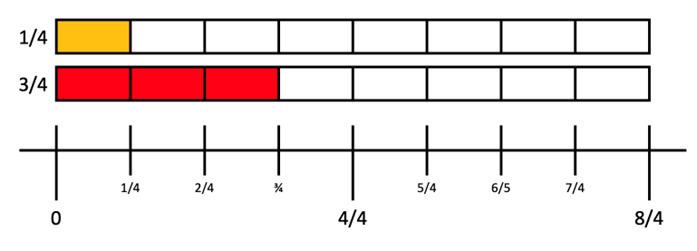
Figure 14 A visual representation to show that 3/4 is larger than 1/4.
What about fractions that have the same numerator, but different denominator? If a whole is chopped into four pieces, each piece will be smaller than when a whole is chopped into three pieces. Students will choose 1/4 over 1/3 only because 4 is larger than 3. Students do not realize that fourths and thirds are different fractions and length relationships are different when dealing with denominators. It is like comparing grapes and oranges. One grape is smaller than one orange, the students must learn to compare the same fruits or find a tool such as a number line to help them compare length. Students may even reason that the fraction is the same size because the numerator is the same, but they must be taught that both numerator and denominator need to be factored in to determine which fraction is larger. However, if we put both numbers on the number line as in the illustration, children will see there is a difference in length and realize that one-third is larger than one-fourth.
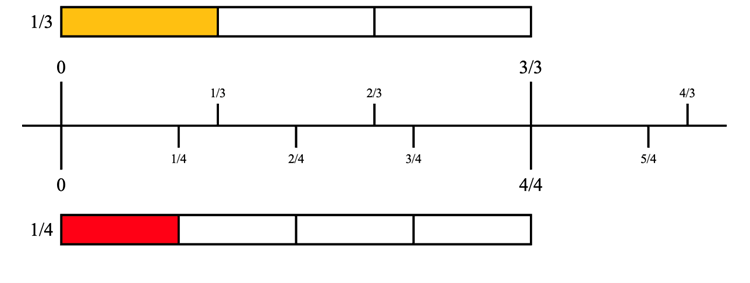
Figure 15 Numerators and denominators need to be factored in to compare fractions.
Comparing Fractions also creates an opportunity for students to see how each fraction grows in length. What I mean is that suppose I compare a whole number to 1/2, 1/3, and 1/4. Students will see that each unit fraction length is a different distance from the origin, 0. What I want students to notice as well is that each number line is chopped into intervals of different lengths. Here you can easily see that as the denominator gets larger, the unit length of the fractions gets smaller: 1/4 < 1/3 < 1/2 < 1. The other crucial point to make is that the denominator describes how many pieces the (k/d) chops up a unit interval (where k is varying, and d is fixed).

Figure 16 - Each unit fraction length is a different distance from the origin, 0.
But what happens when you add another fraction piece? Now each number line increases by one unit interval. When you connect the intervals, it appears that some unit intervals increase in length faster than the fractions that are chopped into smaller unit intervals. Furthermore, when you connect each unit from each number line, it creates a special curve. The interesting part is that both make a smooth, and similar curve.
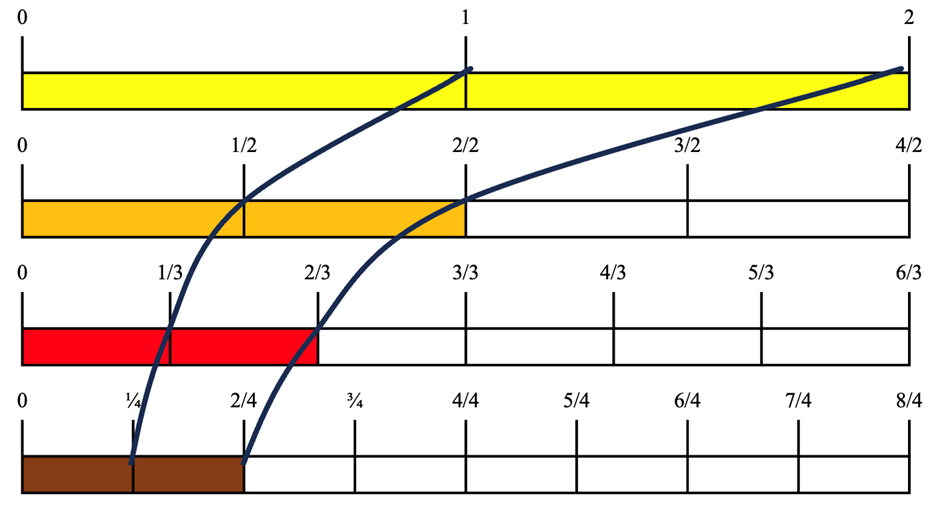
Figure16 A smooth and similar curve appears when you connect each unit fraction from the number line.
Equivalent Fractions
For students to find equivalent fractions on a number line, they must learn to deal with different denominators. Students are used to dealing with whole numbers that are organized using the base ten system. However, fractions do not follow the base ten system. The infinite number of fraction symbols for each number make dealing with fractions redundant. How do we eliminate confusion and redundancy? I will use number lines to help students see what is going on with equivalent fractions and comparing fractions to determine which fraction is larger than another. Now that we have a basic understanding of how to put numbers on a number line and understand that the number line is based on length and distance, let us use these ideas to construct a system of whole number multiples of a given unit fractions.19

Comments: