Transitions in the Conception of Number: From Whole Numbers to Rational Numbers to Algebra

Activities

As the school year starts, students will get used to the format of Eureka Math. Each lesson begins with Fluency and an Application Problem prior to delving into the Concept Development. The progression will begin the second week of school with the Application Problem for Module 1 Lesson 3. I will ask them to create one additional question to go with the Application Problem. Students may work with a partner initially to develop students’ comfort with the process and with mathematical discourse. After a few days, students will be asked to look for and share similarities or differences between the two questions. I plan to carry out this routine throughout the year. By the time we reach Lesson 12 in the first Module, students will be accustomed to creating additional questions and thinking about the similarities and differences between problems.

Activity 1

This activity will coincide with Module 1 Lesson 12. I will teach as described in the Framework for Mathematical Discourse and Schema Building section above. The following day, students will follow the Framework with the problem and data chart (see Table 10). Students will receive the following novel story situation:

Last year on Ted’s farm, his four cows produced the following number of liters of milk:

Table 10: Milk produced on Ted’s farm.

Betsy produced 986 more liters of milk than Buttercup.

Students will work in small, collaborative groups. They will create at least four questions that use one-step addition or subtraction. Once the problems are created, they will create tape diagrams to solve each problem. They will sort them based on the solution path. The process will repeat with two-step problems. Students should create at least three, two-step problems using addition or subtraction. Then they will draw a tape-diagram and solve each problem. Next, they will sort them. The exit ticket will be for the students to write on an index card what they noticed and what they wonder.

Activity 2

The second activity will follow Module 3 Lesson 12 Problem 2 as explained in the Framework for Mathematical Discourse and Schema Building section above. Following the instructional day, the students will be given a novel problem which includes a multiplicative comparison. Students will complete a task using the following situation from Module 3 Lesson 12 Problem 3:

Jayden has 347 marbles. Elvis has 4 times as many as Jayden. Presley has 799 fewer than Elvis.

This time, students will develop as many one-step problems as they can. Then they will solve the problems with tape diagrams and classify the problems according to their operations. As with Activity 1, they will then write two-step problems with addition, subtraction, or multiplication. Students will solve these, sort them, and share out their solutions explaining what they notice.

Activity 3 (culminating activity)

For this activity, students will complete Module 5 Lesson 18 Problem Set #3 through a guided lesson as explained above in the Framework section. The following day, students will have to create a story situation for the following tape diagram:

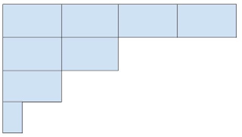
Figure 19: The tape diagram for the culminating activity.

This tape diagram will lend itself to fractions or to multiplicative comparison. Students should be able to tap into the schemas they developed from their previous work and apply them to a novel problem.

Then they will create as many single-step problems as they can in the allotted time. The problems will be solved and sorted. Next, students will create two-step problems that they will solve and sort. Students will complete a poster template provided by me (see Figure 19). For the final section of the poster they will write at least one paragraph explaining what they learned. Additional time will be provided daily to allow students to complete their posters. I hope these projects will become part of the district-wide STEAM Fair.

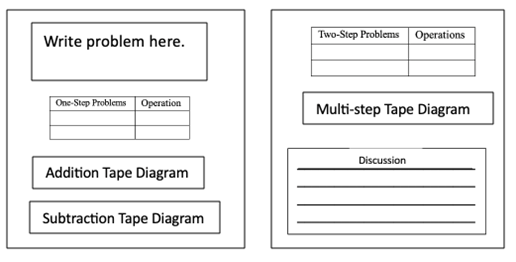
Figure 19: Template for the culminating project