Transitions in the Conception of Number: From Whole Numbers to Rational Numbers to Algebra

Appendix

The Rules of Arithmetic

• The associative rule states that grouping numbers does not affect the result when performing a sequence of additions or multiplications. In other words, you can change the grouping of numbers using parentheses without changing the outcome.

The associative property for addition can be stated as follows:

For any three numbers a, b, and c:

(a + b) + c = a + (b + c)

It is significant that the Associative Rule only involves the simplest possible case of parenthesization but implies equality of all possible parenthesizations. However, establishing this is true involves a substantial amount of logical argument. Similar remarks apply to the Associative Rule for Multiplication.

Similarly, the associative property for multiplication can be stated as follows:

For any three numbers a, b, and c:

(a b) c = a (b c)

• The commutative rules state that the order of numbers does not affect the result when performing a sequence of additions or multiplications. In other words, you can change the order of the numbers being added or multiplied without changing the final outcome, and it can be stated as follows:

For any two numbers a and b:

a + b = b + a

Similarly, the commutative property for multiplication can be stated as follows:

For any two numbers a and b:

a b = b a

• The inverse rule for multiplication states that multiplication and division are inverse operations of each other. That is, division by b is the same as multiplying by 1/b and vice versa. The rule asserts that there is a multiplicative inverse for every non-zero number, meaning that multiplication by the inverse undoes multiplication by the original number (so it amounts to division by the number). Then 1/b is a notation for the multiplicative inverse.



• The arithmetic Inverse Rule for Addition, also known as the additive inverse or the opposite, states that for any real number "a," there exists a unique real number called its additive inverse, denoted as "-a," such that:

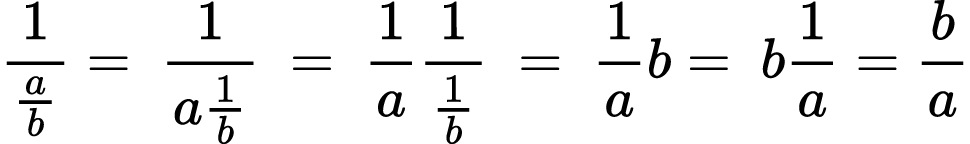
a + (-a) = 0.

In simpler terms, when you add a number to its additive inverse, the result is always 0. This property is fundamental in arithmetic and algebra and helps define the concept of subtraction.

The Principles of Equality

The "Principles of Equality" refer to the fundamental rules that govern equations and mathematical expressions, which are based on the concept of equality and that state that two expressions or quantities that are the same remain the same after being equally added, subtracted, or multiplied. The three main principles of equality in arithmetic are:

• Addition Principle: The resulting equation remains valid if you add the same number to both sides of an equation. In other words,
• if a = b, then a + c = b + c, where "c" is a constant.
• More generally, Equals added to equals make equals.
• Subtraction Principle: The resulting equation remains valid if you subtract the same number from both sides of an equation. In other words,
• if a = b, then a - c = b - c, where a, b, and c are any three numbers.
• This is the addition principle applied to the additive inverse.
• Multiplication Principle: If you multiply both sides of an equation by the same non-zero number, the resulting equation remains true. In other words, if a = b, then a * c = b * c, where a, b, and c are any three numbers. It is unnecessary to require that c be non-zero, although if c = 0, the equation becomes 0 = 0, so it is not interesting. When c needs to be non-zero is when you want to divide by it.

Alternatively, equals multiplied by equals make equals.