Introduction

Teaching mathematics in High School involves multiple challenges. Among these are the lack of students’ interest in learning the subject, the generalized notion that mathematics is a complex subject, and the belief that what students learn has minimum or null real-life applications.  In my teaching experience, teaching word problems is an excellent way to address these challenges.  Although students are not inclined to solve these problems and prefer simple symbolic ones, word problems have two advantages. First, they allow practicing reading comprehension, and second, they open the possibility of solving real-life, engaging, and meaningful real-life problems for the students.

Notably, when solving word problems, the main task is translating the given text into equations (usually just one equation for simple problems) and then solving using algebraic rules. However, even if the first step is successful, students may only be able to answer the problems if they can do the algebraic work on solving the resulting equation. Among all kinds of equations, divisions of fractions cause trouble for my students. Furthermore, research shows that word problems involving fraction division are particularly challenging. For instance, Koichu et al. showed difficulties with the conceptualization of divisions of fractions by investigating the ways of thinking of mathematics teachers (Koichu 2013). The authors showed that problems are successfully solved when the given fractions are perceived as operands instead of reading the problems as a division of divisions, thus opening a path for successful teaching of this topic. These results support earlier findings by Ma, where participants were asked to calculate 1 ¾ ÷ ½.  Notably, almost half of the participants confounded dividing by ½ with dividing by 2 (Ma 1999). Because of this result, Ma highlighted the need to replace the ‘‘uncomfortable’’ division (e.g., a fraction by a fraction) with a ‘‘comfortable’’ division (e.g., a fraction by a whole number).

Similar to these results, I see my Algebra II students confident when solving problems of divisions by whole numbers, while they are not when given problems of solving divisions of fractions. In the latter case, many accept that “new rules” apply for these kinds of problems, which are not clear but, if followed, can produce a correct, although not transparent, answer. An example is when I asked my students to solve the division of 4 by 2, and everyone answered 2. That is, dividing 4 into groups of 2 produced parts of size 2. Next, when asked to solve the division of 4 by ½, many recurred to the symbolic solution of 4 ÷ ½ = 4 * 2/1 = 8, without having a clear idea of what the 8 represented. In this sense, using models like the number line or the rectangle model promoted by the Singapore Ministry of Education can be very helpful (Singapore Ministry of Education 2003). When asked the problem: 4 ÷ ½, this translates to dividing 4 wholes into groups of ½.  One good way, which works for divisions by whole numbers and division by fractions, is to think about dividing a by b by asking, “How many copies of b are in a?”.

This definition of division can be illustrated well using the number line and rectangular models in what is known as the “measurement model” of division. For example, for the above problem, using the rectangular model to solve 4 ÷ ½, we have the following representation in Figure 1.

Or:

4 wholes:

Divided by ½:

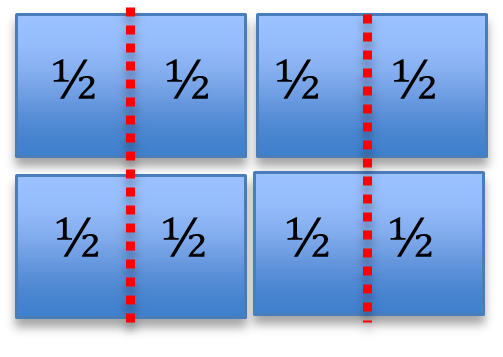
Gives 8 copies of ½ size

Figure 1. The rectangular model represents the division of 4 by ½.

The same procedure works for the problem, 1 ¾ ÷ ½, that is, how many copies of ½ are in 1 ¾, but we will illustrate its solution using the number line as shown in Figure 2.

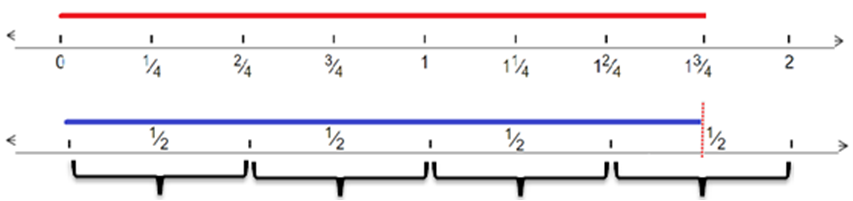
Figure 2. Number lines representing the division of 1 ¾ by ½

In the first number line, the red segment represents 1¾. Next, we have a second number line, marked in intervals of length ½, ½’s, to determine how many copies of ½ are in 1¾. We can see from the blue line that ½ fits 3 and ½ times, which is the answer to our problem. 

These models are visual representations of the division by fractions. They are very much needed to provide a rationale for students of the arithmetic operation, an argument supported by Li, who says that learning mathematics needs to go beyond rote memorization of procedures since its meaning requires explanation through connections with other mathematical knowledge, various representations, and/or real-world contexts like the above-described models (Li 2008).

This unit uses three collections of word problems to teach Algebra II students how to solve real-life applications using one simple algebraic equation whose solution involves the division of fractions.

Rationale

The rationale for teaching division of fractions in an Algebra II class is based on several critical mathematical concepts and real-world applications. Following are some key points:

Fraction Division using the partitioning model

The first insight students learn from the arithmetic operation of division comes from the partition model. For example, if I have six books and need to give them to three students, how many books do each of them get? In this case, we are partitioning a set of six books into three sets, and the answer is two, as each set will have this number of books. However, when we divide by a fraction, the partition model is not very helpful. For instance, how can we interpret the division of 6 apples by 1/2? We need instead to think of division in terms of measurement. In this case, we are given the size of the portions, and the question is, how many portions of ½ apple are there in 6 apples?

Fraction Division using the definition of copies of b in a

A general definition of division reads as follows (Adding it Up 2001). In the division of a/b, where a and b could be an integer or rational numbers, ask the question, how many copies of b are there in a? This general definition is used throughout the unit, reinforcing to the students that it is possible to have a general definition that extends their prior conceptions and is universally applicable to all the problems they may find.

Fraction Division as Inverse Multiplication

From the point of view of the Rules of Arithmetic, the division of fractions can be seen as the inverse operation of multiplication (as shown in the Appendix). Thus, 1/a, by definition, is the result of dividing a quantity (playing the role of a unit) into equal parts.

So, 1/a = a^-1. Then b/a = b * 1/a,

And, (b/a)^-1 = b^-1 (1/a)^-1 = (1/b) a = a/b. All these equations are a consequence of the Inverse Rule, plus the Associativity and Commutativity Rules (see Appendix).

Moreover, in general, just as multiplying two fractions together results in a fraction, dividing one fraction by another also produces a fraction. Since dividing is the same as multiplying by the multiplicative inverse, which is a fraction, this follows from the fact that the product of fractions is a fraction.

Extending Fraction Operations

Algebra II builds upon the foundation of arithmetic and elementary algebra. By introducing the division of fractions, students expand their understanding of fraction operations beyond addition and subtraction, which are typically taught at earlier grade levels. Students also reinforce and consolidate their knowledge of fractions by seeing their application in real-life practical problems which involve their division.

Understanding Fractional Quotients

The learning and practicing of the division of fractions allow students to interpret the result as a fractional quotient. Realizing this is very important since fractions and ratios are generally seen as different mathematical entities when they are equivalent. For example, dividing 2/3 by 1/4 can be interpreted as "How many 1/4-sized pieces can fit into a 2/3-sized piece?" That is, what is the ratio of 2/3-sized pieces to 1/4-size pieces? This idea is essential for working with rational numbers and understanding real-world applications involving ratios and proportions.

Rationalizing Complex Fractions

Algebra II often deals with more complex algebraic expressions, including rational expressions. Division of fractions provides a foundation for simplifying and rationalizing complex fractions, where the numerator and denominator can contain fractions or algebraic expressions. It is common for students to get discouraged when they see problems that involve fractions and even more when they are present in ratios. Therefore, students must learn and practice complex fractions.

Applications in Science and Engineering

The division of fractions has numerous applications in fields such as physics, engineering, and chemistry. For example, calculating rates, proportions, concentrations, and dilutions often involve dividing fractions. Teaching division of fractions equips students with the necessary mathematical tools to solve problems encountered in these areas. The students gain confidence in their mathematical abilities, as they can apply the abstract concepts of mathematics to STEM applications, which can further motivate them to pursue post-secondary education in these fields.

Problem-Solving and Critical Thinking

The division of fractions requires students to think critically and apply mathematical reasoning to solve problems. As noted in the introduction, math is always about understanding problems, especially word problems, where the students need to use their previous knowledge to decode the information, translate it into symbolic expressions, and then form an equation. Significantly, the Algebra problems involving the division of fractions encourage logical thinking, pattern recognition, and the ability to manipulate algebraic expressions. These problem-solving skills are crucial for success in higher-level mathematics and many other disciplines.

Preparation for Higher-Level Math

The division of fractions is a stepping stone to more advanced mathematical concepts. A clear understanding of the meaning of division of fractions, with the use of different visual and symbolic methods, generates an understanding that lays the groundwork for topics like operations with rational expressions, solving equations involving fractions, and working with complex numbers, all of which are covered in later advanced algebra, precalculus, and calculus courses. (Hiebert 1997, Heid 2005)

In summary, teaching the division of fractions in an Algebra II class provides students with a deeper understanding of fractions, promotes problem-solving skills and critical thinking, and prepares them for more advanced math topics. It also offers practical applications in various scientific and engineering fields, motivating the students to pursue these academic fields and contributing to developing a well-rounded mathematical foundation.

Content Objectives

Following are the content objective for this unit. The students will

Understand the Concept of Fraction Division

Students should understand that division of fractions represents the partitioning of one fraction into equal parts determined by another fraction. This understanding will extend the concept to the general definition that division of a/b asks how many copies of b are in a.

Apply the Algorithm for Fraction Division

Students should be able to understand and apply the standard algorithm for dividing fractions, which involves multiplying the first fraction by the reciprocal of the second fraction. Moreover, most importantly, the students should understand the origin of this algorithm from the rules of arithmetic.

Simplify Complex Fractions

Students should learn to simplify complex fractions by dividing the numerator and denominator by their greatest common divisor resulting in a simpler fraction or a whole number. The students will have the opportunity to practice the simplification after they have arrived at the answer to the problems by asking themselves if there is a more straightforward way to express the result.

Solve Real-World Problems

Students should be able to apply the division of fractions to solve various real-world problems, such as scaling recipes, buying products, arranging sets, etc.

Rationalize and Simplify Algebraic Expressions

Students should understand how to rationalize and simplify algebraic expressions involving fractions. This understanding includes dividing algebraic fractions, simplifying rational expressions, and simplifying complex fractions containing variables. In the set of problems that the students will work on in this unit, the rationalization of fractions will be needed when they encounter problems of subtraction of whole numbers and fractions.

Apply Division of Fractions to Ratios and Proportions

Students should be able to apply the concept of division of fractions to solve problems involving ratios and proportions, which are fundamental concepts in STEM applications.

Communicate and Justify Solutions

Students should effectively communicate their mathematical reasoning and justify their solutions when dividing fractions, using appropriate mathematical language and notation.

By achieving these content objectives, students will develop a solid understanding of the division of fractions, its applications, and its connection to other mathematical concepts, preparing them for more advanced algebraic topics and problem-solving in various contexts.

Teaching Strategies

This unit will use three teaching strategies: visualization, real-life context, and practice.

The visualization Strategy

Visual representations help students understand the division of fractions. In particular, the unit uses the rectangular model and the number line to demonstrate the division process. Students can create and manipulate rectangles and number lines, as illustrated in the introduction, to see how one fraction is divided by another, thus making it easier to grasp the concept. Furthermore, most importantly, to visualize the general definition of division presented in the introduction, division of a/b asks how many copies of b are in a.

The Real-Life Context Strategy

The students connect the division of fractions to real-life contexts, making the concept more meaningful and relatable to them. This curriculum unit presents two sets of word problems with real-life scenarios where the division of fractions is applied. For example, students solve problems related to sharing food among friends, dividing ingredients for a recipe, buying fractions of pounds of fruits, and finding the cost of fractions of pounds of produce. Significantly, by contextualizing the division of fractions, students can understand its practical applications and see the concept's relevance in their everyday lives.

The Practice and Application Strategy

The lesson provides ample opportunities for practice and applications, a crucial element when teaching the division of fractions. The unit includes a set of exercises that gradually increase in complexity, starting with problems that only involve integers, in which the students can familiarize themselves with the procedures and then progress to more challenging problems that involve the division of fractions, which is the core of this unit. Students will develop fluency and confidence in dividing fractions utilizing ample practice. Additionally, by incorporating real-world problem-solving tasks, group work, and discussions, students can deepen their understanding which helps them apply their skills in different contexts.

Implementing a combination of these strategies in this unit can enhance students' comprehension and retention of the division of fractions. In summary, by engaging students through visualization strategies, real-life contexts, and practice and application, this unit creates an inclusive and effective learning environment that fosters a strong foundation in this important mathematical concept.

Teaching Implementation

This unit will try to teach students how to translate word problems into the general abstract equation: ax + b = cx + d (Eq. 1), where a, b, c, and d are numbers supplied in the problem and x is the quantity to be found. Problems of this type were studied in our YNI seminar. The unit will include two sets of problems. The constants a, b, c, and d will be integers in the first set. Using the Rules of Arithmetic and the Principles of Equality (presented in the Appendix), the solution of this equation, which applies to all the problems in the set, can be found to be:

Deriving this equation will be a capstone part of my unit and will be carefully presented to my students as follows:

Subtracting b from both sides of the equation

ax + b = cx + d

yields the equation

ax + b - b = cx + d - b,

which simplifies using the Additive Identity rule, b - b = 0, to ax = cx + d - b

Next, subtracting cx from both sides of this equation and using the Commutative and Associative Rules on the right-hand side to put the -cx next to the cx gives the equation

ax - cx = cx - cx + d - b

Again, using the Additive Identity rule, cx - cx = 0, we obtain:

ax - cx = d - b

Using the Distributive and the Commutative Rule of Multiplication, we know that ax - cx = x(a-c). Thus, we have,

x(a-c) = d - b

Dividing both sides by (a - c), we have,

Moreover, using the Reciprocal Identity: , yields the final solution as:

The unit is scaffolded into four progressive lessons, expanding the algebraic concepts. First, the students will work with a set of real-life word problems that only involve constants (a, b, c, and d) that are integers. After the students become familiar with the generation of the corresponding equations, I first want them to find the solutions one at a time. Then toward the end of the unit, I will make the striking and important point that if you work symbolically, there is a universal formula for the solution, equation (2).

Next, the students will work with a second set of word problems, now involving constants that are rational numbers. Another version of equation 1 represents this second set of word problems, specially designed to have rational numbers in it, in which two of them share the same denominator: Eq. 3. This equation has a solution involving the division of fractions,

This can be justified directly, using the general symbolic solution given above, or rederived using the rule for computation with fractions. At this point, the division of fractions will be needed to finalize the problems.  Mathematically, fraction division can be presented as an algorithmic procedure that can be easily taught and learned by “invert and multiply.” The reasons for “invert and multiply” can be, and ideally would be, explained using the Rules of Arithmetic. It should be valuable for students to know that division by a whole number n is the same as multiplication by 1/n, and vice versa. Also, multiplication by a/b is the same as multiplication by 1/b followed by multiplication by a, according to the Associative Rule. (Or things can be done in the opposite order because of commutativity.)

Sharp and Adams recommend that students who can construct personal knowledge using various resources, i.e., pictures, symbols, and words, can improve their understanding and ability to communicate solutions (Sharp 2002). Building on previous knowledge and extending to the division of fractions, this unit aims to build confidence and a deeper understanding of mathematical procedures. This is very important as early teaching should provide realistic situations that enable students to build on their existing knowledge base (Streefland 1991).

The unit then will develop and test many different methods to teach the division of fractions which enrich the understanding of what the mathematical operations mean, following the guidance of several studies which have been conducted to verify the best approaches to teach students the invert-and-multiply algorithm (Elashhab 1978, Silvia 1983). These studies and descriptions of practical lessons rigorously guided students toward the invert-and-multiply algorithm using algebraic (Chabe 1963) and pictorial representations (Elashhab 1978; Silvia 1983) for instruction.

Lessons

The first lesson will last five days, during which the students work for 20 minutes each day, and it is organized in the following way.

• The students copy two-word problems into their notebooks and will start solving them individually. These problems will be from the first set involving only whole numbers, where I used the simplified version for equations 1 and 2, with c = 0, leading to equations 1b and 2b:

ax + b = d (Eq. 1b)

• The teacher asks for a volunteer to read aloud the first problem.
• The teacher asks for a volunteer that gives a hint on how to approach the word problem.
• The teacher solves the problem, step by step, with the help of the students.
  • The teacher will give the students more independence as they progress in solving the problems during the five days of the lesson.
• The teacher asks for a volunteer to reread the problem and explain the solution.
• On the last day of the lesson, the teacher will reveal how all the problems can be solved with the general equation 2.

The second lesson will last another five days, where the students work for 20 minutes each day, and it is organized in the following way.

• The students copy two-word problems, from the second set involving rational numbers, into their notebooks and will start solving them individually. These problems will be from the second set involving rational numbers, where I used the simplified version for equations 3 and 4, with v = 0, leading to equations 3b and 4b:

• The teacher asks for a volunteer to read aloud the first problem.
• The teacher asks for a volunteer that gives a hint on how to approach the word problem.
• The teacher solves the problem, step by step, with the help of the students, reaching the general equation that involves the division of fractions, which will be considered the final answer for now.
  • The teacher will give the students more independence as they progress in solving the problems during the five days of the lesson.
• At this point, the teacher asks for a volunteer to reread the problem and explain the solution.
• On the last day of the lesson, the teacher will reveal how all the problems can be solved with a general equation, similar to what was done for the first set of problems.

The third lesson will last another five days, where the students work for 20 minutes daily, and it is organized in the following way.

• The students copy two-word problems of the second set involving only rational numbers and the solution at which they arrived the previous week, which is written in terms of the division of fractions.
• The teacher will review and illustrate using the rectangular model and the number line to finalize solving the problem.
• The teacher will also show how to use the symbolic model, invert and multiply, compare the three ways to solve the problem and ask for students’ feedback on their preferred approach.
  • The teacher will give the students more independence as they progress in solving the problems during the five days of the lesson.
• At this point, the teacher asks for a volunteer to reread the problem and explain the solution.

The fourth lesson will last another five days, where the students work for 20 minutes daily, and it is organized in the following way.

• The students copy two-word problems of the third set involving only rational numbers, which can be represented by Eq. 3 and whose solution is given by Equation 4.

• The teacher will review and illustrate using the rectangular model, the number line, and the symbolic model to finalize solving the problem.
• The teacher will compare the three ways to solve the problem and ask for students’ feedback on their preferred approach.
  • The teacher will give the students more independence as they progress in solving the problems during the five days of the lesson.
• At this point, the teacher asks for a volunteer to reread the problem and explain the solution.

Classroom Activities

Problem Set I: Problems that only involve whole numbers in the given data and are represented by:

ax + b = d (Eq. 1b)

1. Remy went to the convenience store to get ice cream. She selected four small containers and paid a $20 bill for them. She got $10 in change. What was the price of a container of ice cream that Remy bought?
2. Rosa stopped at a fruit stand to buy some pears. She got Asian pears at $3 per pound. She paid with a $10 bill and got $1 in change. How many pounds of pears did she buy?
3. At the office store, Roger bought some notebooks for $3 each and a package of pencils, which cost $2. The total cost of the buy was $20. How many notebooks did Roger buy?
4. Jeff was window shopping. In one window, he saw a display of neckties arranged in rows of 5 neckties each. Additionally, there were two exceptional neckties on the right-hand side. Suppose there were 32 ties in the window. How many rows of neckties were there?
5. Jeff was window shopping. He saw a display of neckties arranged in 8 rows in one window. Additionally, there were 4 unique neckties on the left-hand side. Suppose there were 60 ties in the window. How many neckties were in each row?
6. A school arranged a picnic on the field day. Every student got a plastic fork, a plastic spoon, and a plastic cup. After giving all students their utensils, there were 30 plastic items left saved for another event. The students were very neat and put all the used utensils in a large trash can. At the end of the picnic, the trash had 300 single-use plastic items. How many students were at the picnic?
7. Jose put some stickers in a sticker book of superheroes. He put five stickers on each page, except for the last one, which took seven, and he used 62 stickers in all. How many pages were in the sticker book?
8. Jose put some stickers in a sticker book of superheroes. It had 13 pages in all. Every page took the same number of stickers, except for the first page, which took two 2 more stickers than the other pages. In all, Jose used 80 stickers. How many stickers were on the typical page?
9. Paula bought five dozen flower bulbs to plant in the garden patch in front of her house. She planted four bulbs along the walkway to the front door. The rest, she arranged in rows parallel to the front of the house. She put eight bulbs in each row. How many rows was she able to make?
10. Clark bought five dozen flower bulbs to plant in the garden patch before her house. She planted four bulbs along the walkway to the front door. The rest, she arranged in seven rows parallel to the front of the house. How many bulbs were in each row?

Problem Set II: Problems that only rational numbers in the given data and are represented by

1. Sara prepares a cake for his mother’s birthday. The recipe requires 2/3 cup of flour for every person. Her little brother is helping her, measuring the flour using a 1/4 cup. He discovers they have 25 measuring cups of flour (or 25/4 cups). After preparing the cake, they have ¼ of a cup of flour left. The cake was made for how many people?
2. Paul buys some pounds of apples at ½ $ per pound. He pays with 5 dollars and receives 2 dollars in change. How many pounds of apples did he buy?
3. Karla buys ¾ pounds of grapes. She pays with 2 dollars and receives 50 cents (1/2 dollar) in change. What is the cost per pound of the grapes?
4. Jill bought 4/5 lb. of grapes at x $ per lb. She paid with a 10-dollar bill and received 2 dollars in change. What is the price of the grapes per pound?
5. Every morning, Mary walks at a pace of 20/7 miles per hour. On Monday, she was planning to walk 4 miles. However, she had to stop when she still had one mile left after she realized she had an early meeting at work. How many hours did she walk on Monday?
6. Peter swims at a pace of 4/3 mph. His trainer programs three hrs. sessions; however, Paul had to stop swimming 30 minutes before completing the session because the summer camp needed a lifeguard. How many miles did Peter swim?
7. Every morning, Elisa serves fruits for breakfast in her school cafeteria. On Tuesday, she noted that students only eat ¾ of each fruit. After collecting all the remainder, she made 12 whole apples. How many fruits did she serve?
8. Carlos sets tables, each with four chairs, for a school dance. He noticed that only 2/3 of the tables were occupied during the party, although these were full. If 20 students did not attend the party out of the 60 invited, how many tables did Carlos prepare?
9. John prepares a jelly for his class. The recipe requires 2/3 cups of the mix for every person, and he has 23 cups of it. After preparing the jelly, he had only 1/3 cup of the mix left. The jelly was made for how many people?
10. Laura bought 8/3 lbs. of avocado at x $ per lb. She paid with a 5-dollar bill and received 1-dollar in change. What is the price of avocados per pound?

Problem Set III: Problems that only rational numbers in the given data and are represented by

1. Maria and John are planting flowers in their respective gardens. Each has chosen a different type of flower, and they plant at different rates.

Maria and John have small gardens in the yard of their apartment building. They both grow flowers, although different kinds. Today, they are planting their gardens. John works more slowly than Maria, but he starts sooner. At the moment, John has planted 2/3 of his garden, but Maria has only planted 1/3. John can plant 1/8 of his garden each hour, and Maria can plant 3/8 of hers each hour. They agree that they will take a break and go for coffee when they have the same portion of their gardens left to plant. How long from now will that be? And how much will each have left to plant? 

2. Alice and Bob drive west on the Mass Turnpike (I90). They are both on their way to a concert at Tanglewood. Alice is driving one (=4/4) mile a minute and has 40 miles to go. Bob drives at 5/4 miles per minute and has 50 miles to go. How long will it take Bob to catch up to Alice? And how far from Tanglewood will they be?
3. Alice and Bob are filling a swimming pool with water from two sources. They each have a different flow rate and want to determine when the water levels from both sources will be the same so they can go together for lunch. Alice's source fills the pool at a rate of 2/5 of the pool's capacity per hour, and she has already filled 1/10 of the pool. Bob's source fills the pool at a rate of 1/5 of the pool's capacity per hour and has already filled 3/10 of the pool.
4. Samantha is selling handcrafted necklaces. Each necklace is priced at 3/4 of a dollar. She has already earned 4/2 dollars today from other sales. Lucas, on the other hand, is selling bracelets. Each bracelet is priced at 2/4 of a dollar. He has already earned 8/2 dollars today from other sales. They are curious to know after how many items sold they will both have the same earnings for the day.
5. Emily is conducting a chemistry experiment in her lab. She wants to have two beakers with the same amount of a certain chemical in both. The chemical is a solute – it is dissolved in water. One beaker already has 5/9 grams of the chemical, and another has 1/9 of a gram. She also has some bottles with the chemical dissolved in different concentrations. Bottle A has 3/7 of a gram of solute per milliliter of solution, and bottle B has 5/7 of a gram of solute per milliliter of solution. She wants to add the same volume of solution from each bottle to each beaker (the bottle with higher concentration to the beaker with less solute), to equalize the amount of solute in the two beakers. How many milliliters should she add?
6. Samantha and Emily are both running on a circular track. Samantha starts at a point of 2/5 on the track and runs at a rate of 5/12 of the track per minute. Emily starts at a point 1/5 on the track and runs faster, at a rate of 7/12 of the track per minute. How long (how many minutes) will it take for Emily to catch up to Samantha?
7. Jamie went to a candy store where all the candies were sold at a fixed price per pound. Jamie bought some hard candies weighing 4/5 pounds and some gummy bears weighing 1/5 = 3/15 pounds. At the same time, Alex bought hard candies that weighed a total of 3/5 pounds and then added a larger type of gummy bear to his purchase. A big gummy bear weighs 4/15 pounds. If Jamie and Alex bought the same total candy weight, how many gummy bears did each one buy?

Solutions to selected problems from Problem Set III.

(1) Let x be the number of hours at which they will have planted the same portion of their gardens; then,

1/8 x + 2/3 = 3/8 x + 1/3

x = (2/3) – (1-3) / (3/8 – 1/8)

x = (1/3) / (2/8)

x = (1/3) * (8/2) = 8/6 = 4 /3 hrs.

(2) Let x be the number of minutes it takes for Bob to catch up to Alice; then,

(4/4) x + 10 = (5/4) x

10 = ((5 /4) – (4/4)) x

10 = (1/4) x

x = (10 / 1) / (1 /4) = (10 /1) *(4 /1) = 40 minutes

The total distance is (4/4) *40 + 10 = 50 miles. Thus, they will be right at Tanglewood!

(4) Let x be the number of items, then,

¾ x + 4/2 = 2/4 x + 8/2

x = (8/2) – (4/2) / (3/4) – (2/4)

x = (4 / 2) / (1 /4) = (4 / 2) * (4 /1) = 16/2 = 8 items.

(5) Let x be the number of milliliters, then,

5/9 +  3/7 x  = 1/9 +  5/7 x 

x = (5/9) – (1/9) / (5/7) – (3/7)

x = (4/9) / (2/7) = (4/9) *(7/2) = 28/18 = 14 /7 ml

Resources

Interactive online number line generator https://helpingwithmath.com/generators/numberlinegenerator01/

Solutions to selected problems from Problem Set I.

(1) Let x be the price of a container of ice cream in dollars; then,

4x + 10 = 20

4x = 20 - 10

x = (20 – 10) / 4 = 10 / 4 = 2.5 $

(3) Let x be the number of notebooks that Roger bought, then,

3x + 2 = 20

3x = 20 -2

x = (20 - 2) / 3 = 18 / 3 = 6 notebooks.

(7) Let x be the number of pages in the sticker book.

5x + 2 = 62

5x = 62 – 2

x = (62 – 2) / 5

x = 60 / 5 = 12 pages

(10) Let x be the number of bulbs in each row, then,

7x + 4 = 5(12)

7x + 4 = 60

7x = 60 – 4

x = (60 – 4) / 7

x = 56 / 7 = 8 bulbs in each row. 

Solutions to selected problems from Problem Set II.

(1) Let x be the number of persons who will get some cake, then,

2/3 x + ¼ = 25 /4

2/3 x = (25 /4) – (1/4)

2/3 x = 24 /4

x = (24 /4) * (3/2) = 72 / 8 = 9 people.

(4) Let x be the price of one pound of grapes.

4/5 x + 2 = 10

4/5 x = 10 – 2

4/5 x = 8

x = 8 / (4/5) = (8 /1) / (4/5) 

x = (8 /1) * (5/4) = 40 /4 = 10 $ / b

(6) Let x be the number of miles Peter swam.

And, time = speed * distance, then,

4/3 x + ½ = 3

4/3 x = 3 – ½ = 6 /2 – 1 /2

4/3 x = 5/2

x = (5/2) / (4/3) 

x = (5/2) * (3/4) = 15/8 miles

(8) Let x be the number of tables Carlos set up, then,

(2/3) 4x + 20 = 60

8/3 x = 60 - 20

8/3 x = 40

x = (40/1) / (8/3)

x = (40/1) * (3/8) = 120 / 8 = 15 tables

Appendix

The Rules of Arithmetic

• The associative rule states that grouping numbers does not affect the result when performing a sequence of additions or multiplications. In other words, you can change the grouping of numbers using parentheses without changing the outcome.

The associative property for addition can be stated as follows:

For any three numbers a, b, and c:

(a + b) + c = a + (b + c)

It is significant that the Associative Rule only involves the simplest possible case of parenthesization but implies equality of all possible parenthesizations. However, establishing this is true involves a substantial amount of logical argument. Similar remarks apply to the Associative Rule for Multiplication.

Similarly, the associative property for multiplication can be stated as follows:

For any three numbers a, b, and c:

(a b) c = a (b c)

• The commutative rules state that the order of numbers does not affect the result when performing a sequence of additions or multiplications. In other words, you can change the order of the numbers being added or multiplied without changing the final outcome, and it can be stated as follows:

For any two numbers a and b:

a + b = b + a

Similarly, the commutative property for multiplication can be stated as follows:

For any two numbers a and b:

a b = b a

• The inverse rule for multiplication states that multiplication and division are inverse operations of each other. That is, division by b is the same as multiplying by 1/b and vice versa. The rule asserts that there is a multiplicative inverse for every non-zero number, meaning that multiplication by the inverse undoes multiplication by the original number (so it amounts to division by the number). Then 1/b is a notation for the multiplicative inverse.



• The arithmetic Inverse Rule for Addition, also known as the additive inverse or the opposite, states that for any real number "a," there exists a unique real number called its additive inverse, denoted as "-a," such that:

a + (-a) = 0.

In simpler terms, when you add a number to its additive inverse, the result is always 0. This property is fundamental in arithmetic and algebra and helps define the concept of subtraction.

The Principles of Equality

The "Principles of Equality" refer to the fundamental rules that govern equations and mathematical expressions, which are based on the concept of equality and that state that two expressions or quantities that are the same remain the same after being equally added, subtracted, or multiplied. The three main principles of equality in arithmetic are:

• Addition Principle: The resulting equation remains valid if you add the same number to both sides of an equation. In other words,
• if a = b, then a + c = b + c, where "c" is a constant.
• More generally, Equals added to equals make equals.
• Subtraction Principle: The resulting equation remains valid if you subtract the same number from both sides of an equation. In other words,
• if a = b, then a - c = b - c, where a, b, and c are any three numbers.
• This is the addition principle applied to the additive inverse.
• Multiplication Principle: If you multiply both sides of an equation by the same non-zero number, the resulting equation remains true. In other words, if a = b, then a * c = b * c, where a, b, and c are any three numbers. It is unnecessary to require that c be non-zero, although if c = 0, the equation becomes 0 = 0, so it is not interesting. When c needs to be non-zero is when you want to divide by it.

Alternatively, equals multiplied by equals make equals.

Implementing District Standards

A.1 The student will

1. represent verbal, quantitative situations algebraically; and
2. evaluate algebraic expressions for given replacement values of the variables.

AII.1 The student will

1. add, subtract, multiply, divide, and simplify rational algebraic expressions;
2. add, subtract, multiply, divide, and simplify radical expressions containing rational numbers and variables and expressions containing rational exponents; and

AII.4 The student will solve systems of linear-quadratic and quadratic-quadratic equations algebraically and graphically.

Works Cited

Chabe, A. M. 1963. Rationalizing “inverting and multiplying.” The Arithmetic Teacher, 10(5), 272–273.

Elashhab, G. A. 1978. A division of fractions-Discovery and verification. School Science and Mathematics. 78(2), 159–162.

Heid, M. K., Blume, G. W., and Clarin, M. V., eds. 2005. Research on Technology and the Teaching and Learning of Mathematics: Research Syntheses. Information Age Publishing.

(This collection of research syntheses may include studies supporting the role of division of fractions in preparing students for advanced mathematical concepts).

Hiebert, J., Carpenter, T. P., Fennema, E., Fuson, K. C., Wearne, D., Murray, H., and Human, P. 1997. Making Sense: Teaching and Learning Mathematics with Understanding. Portsmouth, NH: Heinemann.

(This book delves into the importance of understanding mathematical concepts, including division of fractions, to support later learning in advanced mathematics).

Koichu, Boris, Guershon Harel, and Alfred Manaster. "Ways of thinking associated with mathematics teachers’ problem posing in the context of division of fractions." Instructional Science 41 (2013): 681–698.

Li, Yeping. "What do students need to learn about the division of fractions?" Mathematics teaching in the middle school 13, no. 9 (2008): 546–552.

Ma, L. 1999. Knowing and teaching elementary mathematics. Mahwah, NJ: Erlbaum.

Mathematics Learning Study Committee, Center for Education, Division of Behavioral and Social Sciences and Education, National Research Council; Jeremy Kilpatrick, Jane Swafford, and Bradford Findell, editors. Adding It Up: Helping Children Learn Mathematics. Washington, DC: National Academy Press, 2001.

Sharp, J.; Adams, B. “Children's constructions of knowledge for fraction division after solving realistic problems” Journal of Educational Research.  95(6): (2002): 333-347.

Silvia, E. M. (1983). A look at division with fractions. The Arithmetic Teacher; 30(5), 3841.

Singapore Ministry of Education. Primary Mathematics 6B. Singapore: Times Media Private Limited, 2003.

Streefland, L. (1991). Fractions in realistic mathematics education. Dordrecht l Boston l London: Kluwer.