Astronomy Key Concepts
Before beginning to teach the curriculum unit, students should be surveyed for what they already know about Astronomy and Space Science. Since the goal is to teach algebra by introducing an elementary level of astronomy and space science, some key concepts in Astronomy and Space Science should be discussed.
Temperature Scales
There are three types of temperature scales. The Fahrenheit scale is commonly used in the United States. The Fahrenheit scale is defined by the fact that water freezes at 32°and boils at the temperature of 212°. The Celsius scale is used internationally. The freezing point of water is 0°C and the boiling point is 100°C. The third temperature scale, Kelvin, is used more by scientists. Kelvin is used by scientists because it truly reflects available energy. The Kelvin temperature scale is the same as the Celsius scale, except for its zero point. The coldest possible temperature on the Kelvin scale is 0 K, which is known as absolute zero. The absolute zero, 0 K, is equivalent to -273.15° C. Basically, the Kelvin temperature value is 273.15 degrees greater than its Celsius value.
Students will use the three temperature scales to understand a basic form of conversion and solving for unknown values.
Tf = 9/5 x Tc + 32
Tk = Tc + 273.15
(Tf is temperature in the Fahrenheit scale, Tc is in the Celsius scale, and Tk in the Kelvin scale).
Distance
The measurement of distance is essential in astronomy and algebra. In astronomy, the measurement of distances is vital, and a lot of attention is focused on distances in space. Since the distances in space include an extremely large range of values, astronomers use several different units to describe distances namely, parsecs, light years astronomical units, etc. Students will learn about the measurement of light years and astronomical units as it relates to their world by determining the distances of cars and other objects.
Parsecs
A parsec is approximately equal to 3.26 light years. It is the distance to an object with a parallax angle of 1 arc second. An arc second is 1/60 of an arc minute, or 1/3,600 of 1°. Astronomers use parsecs because it is more appropriate, but light years are used mostly in popular press.
Light Years
The meaning of a light-year is hard for some to grasp because of the common misconception of the meaning of a light-year. Some people use the word light-year out of context. Light-year is not a unit of time, but rather a unit of distance. A light-year is the distance that light travels in one year. The distance of a light-year is 9.46 trillion kilometers (approximately ten trillion kilometers). If you prefer to refer to light-years in miles, then one light-year is about six trillion miles.
Astronomical Units
In astronomy, not only is a light-year used as a unit of distance but astronomers also use another unit of distance, the astronomical units (AU), especially to refer to distances in the Solar System. The AU is defined as the average distance of the Earth from the Sun. The average distance between the Earth and the Sun is about 149,600,000 kilometers or 93,000,000 miles.
Velocity
The term velocity is often used in astronomy and upper level mathematics. Introducing the term in algebra will help students understand and learn a new word that is often used to recognize speed and direction of motion.
The velocity, v, of an object is defined as the distance it travels per unit time, i.e.
V= d/t
Density
Density will be discussed in this unit because it is a formula that is used greatly in science and is relevant to algebra. The density formula allows students to work with substitution and units of volume. Density is usually referred to as mass density. When the term density is used it describes the mass packed into each unit of volume. The tighter the object is packed, the higher the density. The unit of density commonly used is grams per cubic centimeter. The formula for density is d=m/v. Students will use this formula to calculate the density of packed items that is relevant to them such as cereal in a box.
Ellipse
An ellipse is often represented as an oval shape. This curriculum unit allows students to learn about ellipses at an earlier stage in algebra when discussing astronomy. Students will learn that the shapes of bound orbits of the planets in the Solar System are ellipses rather than circles. Discussing ellipses will permit students to learn that it entails a major axis, a minor axis, a center, and two foci. Examples of real-life tangible ellipses should be brought to the students' attention, such as a slice through the long axis of a football and an egg. (Remember that an ellipse is two-dimensional, whereas an egg or a football is three-dimensional).
Newton's Laws of Motion
Newton's laws of motion are a great teaching "hook". The laws of motion should get the students interested in understanding and engaged in the mathematical insight of his second law F =m•a. Discussing Newton's three laws of motion will spark discussion and interest in learning why and how forces affect motion and how it pertains to algebra.
Newton's First Law of Motion
Newton stated in his book Principia, that "In the absence of a net (overall) force acting upon it, an object moves with constant velocity" (Bennett, 134). Newton wrote this based on what he learned from Galileo's discovery that objects will remain in constant motion until some type of force causes the motion to change. He stated that objects will remain in motion at a constant speed and direction if not acted upon by a force. If an object is not moving, it is considered to be at rest with a velocity of zero.
As a teaching hook for Newton's first law students should discuss his first law as it applies to a parked car on no slope, a car traveling along a straight road with no slope, and the sensation of motion that a person does not feel when traveling in an airplane on a flight with no turbulence or any other net force at a constant speed.
Newton's Second Law of Motion
Newton's second law of motion introduces basic algebra, a formula that contains variables and requires substitution. The second law of motion explains motion of an object when force is present. This law allows us to quantify the relationship of the motions of an object when it is acted upon by a force which causes it to accelerate in the direction of the net force. In order to quantify the relationship of an object's momentum and force, we multiply the mass and the acceleration to determine the force (F =m•a). Remember that acceleration means the rate at which an objects velocity changes, which can be a change in speed, and/or direction.
Newton's Third Law of Motion
Newton's third law of motion states that "For any force applied (action), there always is an equal and opposite force (reaction)" (Bennett, 135). The third law of motion helps us to understand how gravity allows us to stand still on the ground. Our bodies exert a gravitational force on the Earth permitting us to stand at rest on the ground; at the same time, the Earth exerts the same force on us, but in an opposite direction.
Kepler's Laws of Motion
Thanks to Sir Isaac Newton, scientists now understand Kepler's laws of planetary motion. Newton explained Kepler's laws as they are relevant laws of motion and are a consequence of the universal law of gravitation (Bennett, 139). Kepler's laws are great examples of the application of a mathematical solution to a scientific theory. Kepler was not only an astronomer but he was also a mathematician.
Kepler's First Law of Planetary Motion
Kepler's first law states that the planetary orbits are ellipses, and the Sun is located at one focus, which disproves the misconception that they are perfect circles. This law allows students to observe that at some points on the orbit the planet is closer to the Sun, and at other times it is farther away.
Kepler's Second Law of Planetary Motion
The second law of planetary motion that Kepler stated was that a planet moves faster when it is nearer the Sun, and slower when it is further away from it. Newton helped explained this law by understanding conservation of angular momentum. This law is illustrated by the fact that a planet on a circular orbit will continue to orbit with no need for fuel, because the radius from the Sun will remain constant. The orbital velocity must stay constant in order to conserve angular momentum. This law is also explained by understanding a dancer when spinning. If the dancer arms are extended out, she will have a large radius but her velocity of rotation will be small. If her arms are brought inward crossing over her chest, then her radius will decrease and her rotational velocity will increase. The formula m•v•r is used to calculate the conservation of angular momentum. The m represents the mass of the planets or object. The orbital speed of rotational velocity is denoted by the variable v. The radius is signified by the variable r. Conservation of angular momentum works with circles and ellipses because the product of m•v•r will remain constant, as long as the radius decreases when the velocity increases or when the velocity decreases the radius increases.
Kepler's Third Law of Planetary Motion
The third law of planetary motion relates the distance of a planet to the period of revolution around the Sun (that is, the length of the year on that planet) by the formula p 2 = d 3. The planet's orbital period in years is denoted by the variable p. The variable d represents the planet's average distance from the Sun in astronomical units (AU).
Kepler's third law of planetary motion is another great way for students to practice substitution in conjunction with learning exponential functions, perfect squares and perfect cubes.
The Doppler Effect
The Doppler Effect is another concept of astronomy that links algebra to science. This effect explains the shifts of wavelength of light emitted by objects that are moving towards or away from an observing object or person. The Doppler Effect affects wavelengths in sound and the spectrum of light. When dealing with sound, the wavelengths are referred to as high and low pitch sounds. Wavelengths are described with the color blue and red when the shift is based on the spectrum of light, often referred to as blue-shift and red-shift. When a light source is moving towards us, the wavelengths will be shorter creating a high-pitched sound or a blue-shift. If the object or light source is moving away from us, then the light is shifted to longer wavelengths producing a lower pitched sound or a red-shift. A popular example used to understand the Doppler Effect is a moving train. When the train is moving towards us, the whistle that the train blows is a high pitched sound, versus the low pitched whistle sound when the train is moving away.
Once again, a formula is used in astronomy where students can apply substitution and solving for an unknown
variable. The Doppler Shift formula demonstrates how symbols are also used to represent the unknown like variables.
The formula is expressed as, 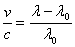 , where v is the object radial velocity, c is the speed of light, Λ
0 is the rest wavelength of a particular spectral line, and Δ Λ, (
Λ ñ Λ 0 ), is the wavelength shift (positive for a red-shift and
negative for a blue-shift). The Doppler Shift formula can also be written as
, where v is the object radial velocity, c is the speed of light, Λ
0 is the rest wavelength of a particular spectral line, and Δ Λ, (
Λ ñ Λ 0 ), is the wavelength shift (positive for a red-shift and
negative for a blue-shift). The Doppler Shift formula can also be written as 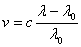 .
.

Comments: