Astronomy and Space Sciences

Lesson Plans

Lesson 1: The 1000-Yard Solar System ¹

Objective: Students will be able to apply proportional reasoning to establish the distances in the Solar System, as well as the sizes of the planets, by converting miles and kilometers to astronomical units.

Purpose:

Materials: Access to a field or parking lot, graphing calculator or scientific calculator, computer with a spreadsheet software

Vocabulary: Miles, Kilometers, Astronomical Units, Yards, Proportional, Convert

Teacher Preparation: Determine where you will conduct the outdoor activity. The outdoor activity can take place on the school's field or the school's parking lot. Once you locate where the outdoor activity will take place, mark off the starting point for measurement for the class.

Have copies of the Mean Distances from the Sun of each planet ready to give to each group.

It is recommended that you complete the activity before giving it to the class, so that you can assist students if they make errors.

Procedure: Have students go outside and measure 100 yards. This is the hook for the lesson. It will get students to think about long distances. Then have students think about distances that are 200 yards long, 500 yards long and 1000 yards long. Next have students work in a group of four and ask them to create a list of the distance they thought of earlier. Once the lists are created, a group representative should share them with the class. Now the students are going to make a model of the Solar System that is based on 1000 yards. The scale will be based on the distance from the Sun to Pluto, which will be 1000 yards.

Using miles and kilometers to convert to an astronomical unit, the ratio will be expressed as 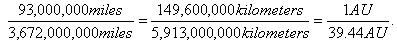. The ratios are all approximately 0.0253.

Since the activity is based on 1000 yards, the students will have to express the same ratio for the scaled distances in the model. Earth distance in yards is not given, so students will represent the distance with the variable x. The distance should be set up as a ratio so it can be calculated. The ratio is represented as 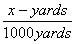. Given that we are converting to astronomical units, have students to set Earth's ratio to equal 0.0253 and solve for x. The steps are listed below:

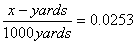
• x = 1000 yards•0.0253
• x = 25.3 yards

Based on the solution above, students now know that Earth is 25.3 yards from the Sun. After finding Earth's distance as a class, have students calculate the distances of the other planets and record the information in a spreadsheet. Give students the mean distances from the Sun in miles and allow them to convert the mean distances in yards and astronomical units.

Mean Distances from the Sun

• Mercury 36 million miles
• Venus 67.2 million miles
• Earth 93 million miles
• Mars 141.5 million miles
• Jupiter 483.3 million miles
• Saturn 886.2 million miles
• Uranus 1782.9 million miles
• Neptune 2792.6 million miles
• Pluto 3672 million miles

Questions: Have students answer the following questions, and submit these answers with their spreadsheets and calculations.

1. If the object representing the Sun were placed at the front of the school, where would the object for Earth be placed?
2. Where would Mercury be placed?
3. Where would Venus be placed?
4. How did you determine where the above planets would be located in the school?

Student Reflection: Ask students to write in their math journals about the mathematics they learned and how it is related to astronomy, our Solar System.

Lesson 2: Finding Our Top Speed ¹

Objective:

1. Students will be able to determine the length of time needed to walk or run a given distance and to plot the data on a graph.
2. Students will be able to determine the distance walked in 8 seconds and to plot the data on a graph and then use the results to develop the concept of slope.

Purpose: This lesson is a hands-on activity that provides a real-world experience, and can be used to start a discussion of travel in the Solar System. By the end of this activity, students will develop an understanding of measuring time and distance.

Materials: Yardsticks or measuring tape, stopwatches, graph paper, index cards, and masking tape.

Vocabulary: Time, Distance

Teacher Preparation:

1. Mark off a hallway or outdoor area distances from 25 feet to 100 feet in increments of 5 feet.
2. Mark the intervals with masking tape.
3. Have an index card for each student with their name to record the number trials and feet they walked in 8 seconds.

Procedure:

1. Start lesson by asking students: "How far they can travel on foot in 8 seconds?"
2. Line up students and begin the trials.
3. The time allowed for walking is held constant at 8 seconds.
4. The distance will vary from student to student.
5. Make sure there is a timer for each student.
6. Each student should record their time on their index card.
7. For multiple trials, use an odd number of trials.
8. Have each student determine their mean distance to record on the class data.
9. As a class make a bar graph of the class data in the frequency table.
10. Be sure to discuss how to label each axis.
11. Discuss where the point will be located on the graph when time is zero and distance is zero.
12. Connect each point on the graph (representing each student distance walked in 8 seconds (0, 0).
13. The steepness of the line shows the rate of speed, or slope.
14. Discuss the concept of slope and give a definition of the slope of a line.

Student Reflection:

Lesson 3: An 8-second Trip ¹

Objective:

1. Students will be able to determine the speed of various toys by conducting experiments.
2. Students will be able to calculate the speed of various means of transportation by using algebra.

Materials: at least one toy car, at least 3 feet of track for a ramp, a board or strong yardstick, tape measure, masking tape, and stopwatches

Vocabulary: Speed, Acceleration

Purpose: The 8-second Trip activity allows students to explore the concept of speed as it relates to travel in space. This is an important activity because it gives students the opportunity to learn about quantify speed and compare rates of speed.

Teacher Preparation:

1. Assemble 3 feet of track.
2. Secure the track to a board in order to keep track straight.
3. Make sure one end of the track is elevated so the cars can roll down.
4. Mark each ramp with a starting point.
5. >Note: The toy cars might not stay in motion for 8 seconds. Have the students to time the cars and calculate the speed of the cars using the formula d=r•t. The average speed can be calculated by using the formula r=d/t. Remember that the elevation of the ramp and other variables can change the speed in the toy car, which affects the time. The stopping time for the car will not be exactly 8 seconds, although the title is "An 8-Second Trip".

Procedure:

1. Start a discussion with students about ways to travel fast and record some possible ways.
2. Before students break into their groups, have them complete a few trials to determine a reasonable time for the car to travel down the ramp. This will determine the interval that all groups will use as a constant in the data, for example 6 seconds.
3. Group students into teams of four for the data collection.
4. Groups should determine one student to be the car starter, recorder, and two timers.
5. Each group should describe its ramp with the ratio of the height of the ramp to the horizontal length of the ramp.
6. Groups should collect three to five sets of data (each group must do the exact same number of trials). Students will be measuring the distance traveled over the agreed constant time.
7. Each group is required to collect data on three ratios of a ramp (1/3, 1/4, and 1/5). Before they begin have them predict which ramp will produce the highest speed and ask them to explain why.
8. Have the students organize the data in a spreadsheet describing the ramp ratio, trail number, distance in feet, time, and average rate of speed.
9. Have groups compare their data with other groups and compare predictions.
10. As a class discuss Newton's Laws of Motion. Make sure students understand that acceleration is the change in speed.
11. At this point if the class is ready, introduce the Pythagorean Theorem.

Student Reflection: Have students to write about how this activity is related to them in the real-world and why Newton's Laws of Motion is important.

Lesson 4: Investigation of a Scientific Quandary ²

Objective:

1. Students will be able to use scientific notation to represent numbers.
2. Students will be able to convert numbers to scientific notation.

Materials: Graphing Calculator

Vocabulary: Scientific Notation

Teacher Preparation:

1. Create two lists of numbers. One list should contain numbers represented as scientific notation. The second list should be numbers not in scientific notation.

Procedure:

1. Give students two lists of numbers. Have students classify the numbers in scientific notation or not.
2. Students should explain how they determine the classification of each number.
3. Students should define what it means for a number to be in scientific notation.
4. Now have students use their graphing calculator's scientific notation mode to help them figure out how to convert standard notation to scientific notation and vice versa.
5. Give students a series of numbers to convert to scientific notation and from scientific notation.
6. Have students answer the following questions:
7. How is the exponent on the 10 related to the number in standard notation?
8. How are the digits before the 10 related to the number in standard notation?
9. If the number in standard notation is negative, how does that show up in scientific notation?
10. Have students write a set of instructions for converting 415,000,000 or a number of your, the teachers, choice from standard notation to scientific notation.
11. Write a set of instructions for converting 6.4 x 10 ⁵ from scientific notation to standard notation.

Student Reflection: Have students write what is the difference between a number in scientific notation and standard notation. Ask students to think about what situations are best for using scientific notation.

Lesson 5: Temperature Scales ³

Objective:

1. Students will be able to use two or more transformations to solve an equation.

Materials: three to five real-world word problems that involve temperature.

Vocabulary: Fahrenheit, Celsius, Kelvin, Temperature

Teacher Preparation:

1. Find at least three real-world word problems that involve temperature.

Procedure:

1. Have students convert each problem to the two temperature scales that the temperature is not given in.
2. Ask students if any of the temperatures indicates freezing temperature.
3. Ask students if any of the temperatures indicates boiling point.
4. Give students the following problem and ask them to convert the Earth's surface and crust to Fahrenheit and the Kelvin scale.
5. The temperature within Earth's crust increases about 30° Celsius for each kilometer of depth beneath the surface. If the temperature at Earth's surface is 24°C, at what depth would you expect the temperature to be 114°C? (Formula: Temperature inside Earth = Temperature at Earth's surface + Rate of temperature increase x Depth below surface)

Student Reflection: Explain how to convert one temperature scale to another temperature scale.

Lesson 6: The Doppler Effect ⁴

Objective:

1. Students will perform an experiment that will demonstrate the Doppler Effect.
2. Students will use substitute given values into the Doppler Effect formula to determine the object radial velocity or the speed of light.

Materials: splash out ball, 9 volt battery, 9 volt battery clip, rope, making tape, electronic noise making mechanism with pure tone (can be purchased from an electronic store)

Vocabulary: Doppler Effect, radial velocity, rest wavelength, spectral line, wavelength shift, red-shift, blue-shift

Teacher Preparation:

1. Prepare the ball before class.
2. Twist the splash out ball open.
3. Thread one end of the rope through the holes of the splash out ball.
4. Tie the end back to the rope.
5. Twist the wires of the electronic noise making mechanism together with the wires of the battery clip.
6. Plug the battery into the battery clip.
7. Tape the assembly to the inside of the splash out ball.

Procedure:

1. Allow one student to twirl the Doppler ball assembly in a circle above his or her head. Make sure the ball is able to gain enough speed.
2. Observers should record and describe what they hear as the Doppler ball move towards them.
3. Have students to record and describe what they hear as the Doppler ball moves away from them.
4. Allow other students to twirl the Doppler ball, and ask them to record and compare what they heard as they twirl the Doppler ball.
5. At the end of the experiment discuss with the class what they heard as the ball approach them and make a class list.
6. Ask students what they heard as the ball passed them and record the information in another class list.
7. Ask the students who twirled the ball did they hear the Doppler shift and ask them to explain why or why not to the class.
8. Relate the experiment to other real-world sounds by asking them if they can tell which way an emergency vehicle is traveling by the pitch of its siren. What about a train? What about a car with the music and base turned up loud?
9. Discuss with the students the phenomenon of The Doppler Effect. You should explain to them the meaning of The Doppler Effect.
10. Explain to the class what is meant by red-shift and blue-shift.
11. Explain the formula for The Doppler Effect and what each variable represents. Make sure that you explain that Λ - Λ ₀can also be written as Δ Λ. By explaining the relationship, it will help prepare students for calculus and physics that Δ is the rate of change.
12. Give the students a series of known values for the formula and ask them to determine the radial velocity or the speed of light value.

1. The rest wavelength of one of the visible lines of the hydrogen is 656.285nm. This line is easily identifiable in the spectrum of the bright star Vega, but is appears at a wavelength of 656.255nm. What is the radial velocity of Vega?

Solution: Remember that a light-year is the distance covered by light, traveling at a speed of 300,000 kilometers per second, in a time of one year. Since the line's wavelength in Vega's spectrum is lightly shorter that its rest wavelength, the line is blue-shifted and Vega's radial motion is moving toward us.

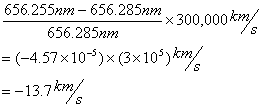
2. In hydrogen, the transition from level 2 to level 1 has a rest wavelength of 121.6nm. Suppose you see this line at a wavelength of 120.5nm in Star A, at 121.2nm in Star B, at 121.9nm in Star C, and as 122.9nm in Star D. Which stars are coming toward us? Which are moving away? Which star is moving fastest relative to us (either toward or away from)? Explain your answers without doing any calculations. Determine the radial velocity for each star.

Student Reflection: Ask students to write in their journals about what they learned today during the experiment. Also, ask them to write about how math is related in astronomy and in a simple real-world activity.