Classroom Activities
Activity One – Translating Expressions
An expression is a recipe for a calculation. Expressions can be represented in a verbal sentence as well as a mathematical sentence. In this lesson, students will practice translating back and forth between the two forms.
Students will begin by playing a number trick. Tell students to choose a number. Multiply the number by 2. Add 14. Multiply by 3. Divide by 6. Subtract the original number. All students should end up with a final answer of 7. Students will work in groups of 4 to discuss why everyone ended up with an answer of 7.
Vocabulary Background: Students will work with their assigned group to define important vocabulary. All members of the group should be able to give an accurate definition, use the word correctly in context, and give an example. The words students will define include: sum, total, increased by, more than, difference, decreased by, less than, product, twice, half of, third of, quotient, ratio, square of, cube of, consecutive, even, odd. Students who finish early will look for synonyms of given vocabulary as well as other relevant terms not mentioned on the list.
Once students have finished defining the vocabulary. I will put up problems to practice the use of the vocabulary. Students will volunteer different math sentences to express the given problem.
Example: 8 + 5 = 13. Possible Responses: The sum of eight and five is 13. Five more than eight is thirteen. Eight increased by 5 is thirteen etc…
Students will set up 2 columns in their notes. At the top of column one they will put Verbal Expression and at the top of column two they will put Mathematical Expression. If the given problem is in the form of a verbal expression, students will write the mathematical expression. If the problem is in the form of a mathematical expression, students will write the verbal expression. Students should not copy the given problem. For homework students will take their notes home and write the missing expressions, which will match the original problem set.
Example:
1. Take a number, multiply by 2, add 3.
2. 5(x + 4)

Next students will work with a partner to write Recipes for Calculations. I will do the first one on the overhead with the students. Take a number and add 7. Multiply by 3. Decrease the number by 4. Multiply by 3 times the number. Students will write both the directions and the expression on their paper. Then with their partner they will write 3 – 5 Recipes for Calculations. Once most students have finished they will then partner up with another group of 2 students. Each group will take turns reading their recipe, while the other group writes the expression.
To close, I will give students two number tricks. Since these tricks are following the activity Recipes for Calculation, I think more students will be able to use the skills to identify why the trick works. Trick: Choose a number. Add 12. Multiply by 2. Subtract 18. Add the opposite of your original number. Subtract 6. This will leave students at their original number.
Trick: Choose a number. Add 7. Multiply by 4. Subtract 14. Divide by 2. Subtract the original number. I will be able to tell students their original number by subtracting 7 from their final answer.
Students will spend the rest of the period working with their assigned group to try to figure out the number trick.
Activity Two – Model Drawings of Arithmetic Rules
All students will be given graph paper for the drawings. The purpose of the activity is to visually show students why these properties work.
Commutative Property Model
Students will fold the graph paper into three sections. The first section will be labeled Commutative Property. Students will begin with the problem 4 + 6. The numbers will be colored so students will use their colored pencils to match the color of the box with the color of the number. They will begin by writing the problem across the top. Then the students will color 4 red boxes and 6 green boxes. Students will then represent the Commutative Property by writing the reverse 6 + 4 and coloring in the corresponding boxes. Students will then be given a blue strip of paper, an unknown amount, which will be represented with the variable x. They will then write the expression x + 7. Students will color in the x boxes blue by lining the strip of paper up on the graph paper to see how many boxes should be colored and then adding an additional 7 orange boxes. Then to show the Commutative Property students will write the expression 7 + x and color in 7 orange boxes and then line the blue construction paper up to color in the x unknown boxes blue.
Associative Property Model
Students will label the second section Associative Property. Again students will color to match both numbers and variables. They will begin with the problem (3 + 2) + 4. They will begin by coloring in the corresponding number of red, blue and green boxes. Then students will take their pencil and shade over the three red boxes and the two blue boxes to show the grouping of 3 and 2 in the parentheses. For the second problem, 3 + (2 + 4) students will color the boxes the same, however this time they will shade over the two blue boxes and the 4 green boxes to show the grouping of 2 and 4. Students will follow this same procedure when given the problem (5 + x) + 3 and 5 + (x + 3). Again they will be given a strip of paper to measure boxes for the unknown, x, amount.
Distributive Property
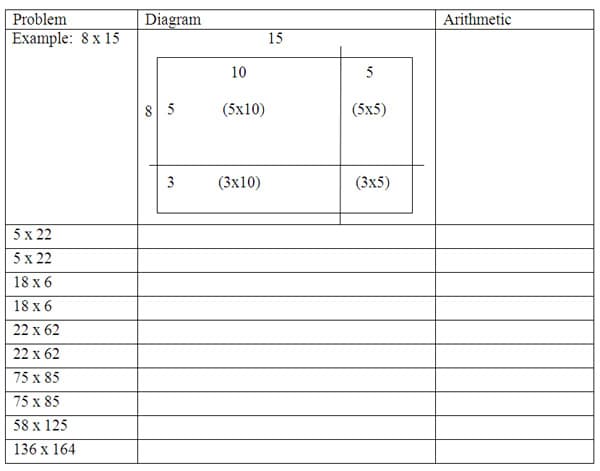
The third section of the paper will be labeled as the Distributive Property. Students will start by sketching a 4 by 6 box on their paper. They will identify the problem as being 4 x 6 and the solution as 24. Then students will draw a line down the center of the box, breaking it up into two 4 by 3 boxes, each with an area of 12. Students will see that the area didn't change. We will write the second problem as 4(3 + 3). Students will then draw a 12 by 8 box and look for different ways to break up the boxes. I will put several charts of the 12 by 8 box on the board. Different students will show how they divided the box and how they calculated the area. While students are working I will walk around and encourage some to try breaking the 12 and 8 up more than once, for example (4 + 5 + 3) (3 + 5). Students who present on the chart paper will explain the drawing as well as show the arithmetic they used.
Then we will move to two-digit multiplication. Students will draw a box that is 25 by 45. They will then break the box into 20 and 5 by 40 and 5, hence creating four different rectangles. They will find the area of each individual rectangle and then add the areas together.
Students will then complete the following problems by drawing a rectangle and breaking it into smaller rectangles. Each problem will need to be solved 2 different ways, both containing a diagram as well as the arithmetic to show the solution.
Activity 3 – Word Problems
This lesson will focus on reading and understanding word problems. Students will be able to label each numerical value, identify the unknown, and write a complete sentence to answer the question.
Students will begin by working in their groups on the following two problems. They may solve them any way they choose. Each member of the group should be prepared to give the explanation.
Problem 1: The cost to rent a sailboat from Ocean's Rental Company is $120 plus $60 per day. If Marco paid a total of $360, for how many days did he rent the sailboat? 7
Problem 2: The local cell phone company charges a monthly fee plus an additional $0.05 per text message. Margo sent 60 text messages this month. If her bill was $33, how much is the monthly fee?
Problem 3: Caper's Carpets charges $100 plus $0.25 per square foot to clean carpets. The carpet in Jackson's house covers 1,000 square feet. If Jackson has saved $200, how much more money does he need to get his carpets cleaned?
Students will then be given the opportunity to share their answers and methods for arriving at such answers. Student answers will not at this time be evaluated as right or wrong.
I will discuss with students the importance of analyzing and understanding a word problem before applying mathematical operations to calculate a solution. So as a class we will work through the information in the problems without calculating solutions. Students will be evaluated on their ability to describe the problem and the information in the problem. During this activity the final solution will not be required. Tomorrow's lesson will focus on building the equations to solve the problem.
As a class we will work through the first problem answering the following questions.
1. What is the question asking?
Response – How many days did Marco rent the sailboat?
2. Write a complete sentence for the solution.
Response – Marco rented the sailboat for ________ days.
2. Identify all numbers and what they represent in the problem.
Response – $120 = Cost to rent the sailboat. $60 = cost per day to rent the sailboat. $360 = total amount Marco paid to rent the sailboat.
3. Explain a method that could be used to solve this problem.
Response – Marco started by paying $120 to rent the sailboat, then he had to pay an additional $60 for everyday he rented the sailboat. So starting at $120, I could keep adding $60 until I got to $360 and see how many times I had to add $60.
Students will answer the same questions for problems 2 and 3. The assessment for this assignment will be identifying key pieces of information, not a numerical answer.

Comments: