Great Ideas of Primary Mathematics

Rationale

Fractions are a lot like fruitcake. A few people like them, but most greet their presence with something between a blasé and a bubonic reaction. Also, akin to a fruitcake, a fraction is made up of multiple parts, and those subparts can be seen as having yet more subparts (which those who do not like fractions find just as unappetizing), yet together they constitute a dense, singular entity. Ultimately the choice of what to do with a fraction, like a fruitcake, varies between consuming it as a whole, nibbling only as little as one must to be polite, or, as many students studying mathematics in our schools are prone to do, throwing it away and looking for something else to eat.

To get beyond metaphor, what I hope you might have a mental image of for a fraction, is some numerator and denominator pair with a line segment in between. If we say "fraction" in general these may be any values, but if we qualify it as a "rational fraction" we signify having integer values for each; possibly with variables standing for integer values, e.g. a/b, as we are often given as a model in algebra texts. ¹ I am hoping you've pictured this because it is "rational fractions" that I want to discuss most in this paper, though I commonly say "fraction" in much of the text below.

Fractions are an important, common form of written rational numbers. When we state that a number is rational we intend to state that it represents a "ratio," between other numbers or quantities, not that it is "reasonable." ² Indeed, for my students, they can seem quite unreasonable to work with them at times.

Over the past five years I have taught mathematics for students from 6 ^th through 12 ^th grade in a variety of secondary curricula. In every course I have taught, students have expressed frustration and confusion with fractions, and their success with mathematics study has been demonstratively hampered by poor skills in managing fractions. In the coming school year I will teach Algebra 1 and Algebra 2 courses at a magnate school for the creative and performing arts. Two of the more pronounced challenges to teaching secondary mathematics in this academic environment have been: 1) students falter with some primary skills to such a degree that it prevents their segue into secondary studies; and 2) many students I teach, who are artists and generally more inclined to humanities, have found secondary math courses to be unengaging and/or inaccessible.

I see fractions as an ideal vehicle to help my students attain more mastery of a ubiquitous topic from their primary skills, while at the same time using this mastery to find engagement with and access to algebra and advanced secondary studies. I will approach this by first considering some difficulties that my students have had with notation, language, and the way in which they have studied fractions in their primary school experience. Then I will state objectives and present strategies, with specific examples of assignments that I will use and other teachers may find helpful.

Notation of Fractions

The mathematical notation of a fraction can be very confusing to students, simply because it uses two value symbols (i.e. numerator and denominator) to represent a single value in a unified symbol (the rational fraction). As with any number and its symbolic representations, when we start to apply its value we discover that it can represent many types of complex relationships in many contexts. What started as a simple little alphanumeric bit of data can become very bewildering, very quickly.

According to an unofficial theorem of mathematician Roger Howe, the power of mathematics lies in its ability to compress large amounts of information into relatively very little notational space. ³ The symbolic form for any particular number has the ability to represent virtually any quantifiable thing. Equations and formulae have the capacity, in brief sets of alphanumeric sequences, to describe, organize, and predict results for vast, vast amounts of data that might otherwise require page upon page of verbal explanation.

The use of fractions allows helpful compressing of information in mathematical notation, but in the power that they bring to compressing, they create new challenges for the mathematics learner by way of the necessary, inverse acts of decompressing that information. Because the fractional notation can serve to represent many possible relationships, students are faced with a paramount task of interpretation and evaluation of multiple, potentially valid meanings when they "unpack" the compressed notation.

In the most basic sense, there are three key ways in which we might consider what the notation of fractions "looks like" to students. The first is illustrated in the following sequence. It has what I believe is an obvious clue to part of the problem students have with fractional notation:

1 + 2 + 7 + 1/5 + 6 + 4 + 4/5 = ?

As we read from left to right, we begin making easy progress until we meet the first fraction. Our "horizontal road" is suddenly obstructed by a "vertical wall." In the midst of what has become an intuitive act of adding numbers, even we who are teachers of mathematics must take a subtle pause, and decide what to do.

We can attempt to keep on flowing and allow the fraction to tag along on our current sum, forming a mixed number in transit. We can use the associative property of addition to regroup the integers in one summation and the fractions in another summation. We can also modify the given notation, either rewriting the integers as improper fractions with the denominator of 5 and the appropriate numerators for equivalent values or rewriting the fractions as the decimals 0.2 and 0.8 respectively.

Going through each of these processes successively is something that could serve as a reasoning exercise for students. Finding the sum of the problem is not meant to be difficult, but if we ignore the fact that it demands choices on the part of our students, even secondary students whom we expect to be competent with such primary tasks, then we may well miss the chance to identify their difficulties with fractions.

The second note that I want to make about the writing of a fraction is really a matter of typography or calligraphy. We might take for granted that the following three forms of fractional notation are interchangeable, but some students infer greater significance around the variations:

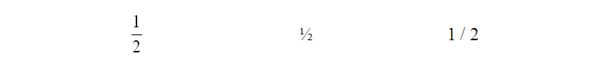
The first, in the most vertical form, typical of the numerator "over" denominator conceptualization does not bear any functional difference from the second, in which the bar separating the "top and bottom" is diagonal and seems to condense the fraction (which could be seen as fixing it as a rational number). The third form can indeed be interpreted as more strictly representing "division of 1 by 2" than the first and second forms, but, for all that, it does not limit those other forms from representing the same division. It is also possible that the third form was necessitated by a word processing issue or the result of a style choice and had the intention of representing a rational number. Ignoring these variations in notation might be another missed chance at helping a student in accurately decompressing the meaning of a fraction.

The third issue that I call attention to in the notation of fractions is the misapplication of the decimal form. Whether it is because students use calculators so frequently and so early in their math classes, as I am inclined to believe, or because they see a unifying quality in the place value notation of decimals, as a continuation of that which they use for units, tens, hundreds, etc., students gravitate in large part toward decimal forms as a means of dealing with fractions.

In cases such as the example above, i.e. when an option was to convert to 0.2 and to 0.8, there were no units or context to refute this interpretation of the abstract and the conversions gave exact values. Confidence in this always being true is dangerous, e.g.:

1/3 of 1002 participants in a poll voted for candidate A. How many voted for A?

The tendency to convert 1/3 to 0.3 can lead to real problems of accuracy, since 0.3 converts far too neatly back to 3/10 and would tell us that 300.06 of the participants voted for candidate A. Converting to 0.33 might seem better, but it converts back to 33/100 and would tell us that 330.66 voted for A. Adding more places of significance, e.g. 333/1000, etc. would close these estimates in on the actual value of 334, which we get by properly applying a reasoning of 1/3 of 1002 participants, but this exhaustive approach would be an inefficient and ironically futile considering that students are trying to avoid such burdens.

If students have a strong enough conceptual understanding they will be able to directly divide 1002 by 3 and be successful in both the mitigation of a fraction and in processing the problem with respect for units and context. The moment when students so much as lay eyes upon the notation of a fraction they run into issues, before any mental processing of values even begins. Resolving this issue requires both visual and verbal understanding.

Language of Fractions

Students often do not feel ownership of the language that is used in mathematics and this is certainly true of their work with fractions. While many are able to phrase ideas in terms of "over" and "under," "out of," or "above" and "below," those students who struggle with proportional reasoning do not usually make effective or accurate use of formal terms descriptive of fractions, e.g. "ratio," "proportion," "quotient," "dividend" and "divisor," or of "reciprocal" and other important terms that arise in our consideration of fractions.

There is, fortunately, some language related to fractions that students are comfortable with and these terms may reveal clues about what we can do to help students find comfort with math jargon that surrounds fractions. Perhaps the most obvious and oft used examples are those of money. A "quarter" of a dollar is of the most accessible fraction for secondary students that we can expect. Another example is a "half" gallon, be it of milk, orange juice, or other product measured by volume. What makes these fractions easy while others are more difficult? The obvious answer might include the fact that these fractions are embodied in our everyday life by tangible objects, but there is more to it.

I suggest two aspects of these fractions that make them more easily understood than others. First, they are verbally managed numbers that can be used without necessitating a numeric representation through which to be interpreted. Second, at the root of this verbal, relative ease with quarter dollars and half-gallons is the fact that their names and their measures have become units unto themselves, such that we do not necessarily think of them as subdivisions or parts of greater whole units.

It would rob these student understandings of value if they were merely a convention of speech and students could not manage their use mathematically. However, there is ready understanding in the majority of students that there are 4 quarters in a dollar and 2 half-gallons in a gallon, so the automaticity that students demonstrate with these fractions is not a mere naming scheme, but also exemplifies that they are fluent enough to apply the appropriate multiplicative inverses. I believe we can use these verbal and 'stand-alone-unit' qualities to build student understanding of all fractions.

Language plays some other obvious, but critical roles in students' fraction management. Students struggle with fraction-word problems because they have not practiced them in significant contexts. ⁴ This is especially detrimental for secondary students developing proportional reasoning because although the application of fractions, usually in the forms of percentages, are presented as statistics in a variety of ways but without a real analysis of their values or what they mean in context.

As a last thought on language, it is important that students simply understand "what" they are studying. In his book Innumeracy, mathematician John Allen Paulos introduces what he considers some of the worst misconceptions about mathematics, the second of which is that mathematics is a completely hierarchical subject in which one topic or skill set follows another without commingling. ⁵ Students' general notion that they are learning "normal math" for years, and then suddenly are doing things like "algebra," works against their comprehension of the grand scheme in which they are working. Students should learn the terminology to appropriately consider their "math" studies.

According to Howe, "We will do well to regularly point out to students the methods we employ that are part of arithmetic and where and how they transfer to skills we would appropriately term algebra." ⁶ This could be very helpful to students in finding the nuances within the reiterated skills of managing fractions, because students might better understand a step forward is not an abandonment of previous skill sets.

Primary Approaches to Managing Fractions

Liping Ma, an international education researcher, claims that students use among three approaches to developing arithmetic skills: counting, memorization, and, what Ma calls, "extrapolation," by which she means a development of reasoning around properties of numbers (which are actually informal applications of both arithmetic and algebra), which is reliant upon student rigor, but neither upon the exhaustiveness of counting nor the inflexibility of memorized facts.

Students struggling with extrapolation in general are all the more prone to struggles with fractions, thus our efforts to address fractions in the algebra environment need to go beyond yet more attempts at rote learning of algorithms or drill practice for dealing with fractions. Of course, there does need to be forethought for the time that any version of an extrapolation approach requires. Ma points out that it relies not only on students having prior experience in taking this "open-ended" attitude toward learning new skills, but also additional time at each stage of study… implying efforts throughout algebra studies.

When we have difficulty justifying extrapolation, over algorithmic approaches, to administrators or skeptical colleagues, we do have some very supportive statements via the NCTM: "National Council of Teachers of Mathematics asserted in their Curriculum and Evaluation Standards (1989) that proportional reasoning is of such great importance that it merits whatever time and effort must be expanded to assure its careful development." ⁷ In other words, learning how to manage fractions is worth the time. I also hope to show in my strategies below that it can be coordinated in coursework so that it needn't "take time away from" learning algebra skills.

We should also expect lasting rewards for this investment of time. The perspective of solving the known from the unknown, i.e. using an open-ended problem solving approach based on what we know with confidence v. unqualified algorithmic exertions, initiates a lasting attitude toward learning and mathematics. ⁸ If this type of attitude toward the notation and communication of rational numbers can be established through work with fractions, it can only be a positive reinforcement of a similar attitude toward all algebra work that involves them.

The beginnings of primary mathematics education, thus the beginnings of arithmetic, rely on "perceivable quantities," numbers that students have a working sense of (i.e. 1, 2, 3…). ⁹ As students enter algebra studies, we must recognize that for many of them fractions are not perceivable quantities. In order to make fractions perceivable, students must understand them via those integers that constitute their numerators and denominators, and from a proportional sense of the unified symbol.

Susan J. Lamon wrote the book on teaching fractions (well "a book," but an incredible one) in which she says, "Understanding fractions marks only the beginning of the journey toward rational number understanding, and by the end of the middle school years, as a result of maturing, experience, and fractional instruction it is assumed that students are capable of a formal thought process called proportional reasoning." ^{1 0} This assumption, though it would be lovely to be able to hold on to, is clearly invalid in many cases. Rather than taking a reactionary approach toward primary skills that we find lacking in our students, we need to be proactively incorporating them into our pedagogy.