Background
Fermi problems are a class of estimation problems that rely on taking a set of justified assumptions and extrapolating them into estimates in order to answer a “big” question. The classic example asks students to estimate how many piano tuners are in Chicago. This can be answered by making some assumptions about how many households are in Chicago, what fraction of households have pianos, how often they need to be tuned and how much work an individual piano tuner can do. If the assumptions you make are carefully documented, you can arrive at a surprisingly accurate result, even with no explicitly given information. Even if individual estimates aren’t great, the accuracy comes from the hope that some estimates will be high, some estimates will be low and on average, the effects will balance each other.
This style of question is indicative of the types of questions students naturally generate on their own or encounter in higher education and the workforce. There’s a research component, an intuition component and the idea that no one is going to hand you the “given information” and check your result against an answer key. Using Fermi problems, we can develop independent problem solving skills in students that will empower them with the ability to ask and answer questions for themselves. The ideal outcome, then, becomes students who not only revel in the challenge of solving new problems, but also seek to ask new questions of the world around them. These questions can then be posed, pondered and traded with other like-minded problem solvers.
One of my favorite published collections of this type of problem appears in Weinstein and Adams’s book Guesstimation. Their problem selection is interesting and engaging. They address some of the “historic” Fermi problems and they provide a good framework for approaching them. Each question comes with a full solution, as well. The approach they outline, however, is somewhat casual and doesn’t quite hit all of the skills I want my students to gain, so below I’ll break down what I want them to get out of this unit in a more systematic fashion.
Problem Decomposition
Fermi Problems are presented as questions. They ask for a specific answer, but typically don't provide (or even hint at) the path to get there. Students, then, should be able to trace back from a request for information to the necessary pieces that comprise the final quantity. I'll refer to these pieces as constituent quantities for the remainder of this unit. Students then combine these pieces to assemble the final calculation that gives them their answer.
Identifying constituent quantities is the bulk of the battle for my kids. They're making a shift from being provided with information that can be arranged and assembled to form an answer to a world where a request is made and the appropriate information to arrive at the solution is not specified. They are making the decisions about what information is important to their calculation and what information is not, because the importance of a number can't be inferred from the fact that it was or was not provided to them in the problem itself. A task I’ve found helpful is to ask my students make a list of information that might be important. There's no requirement to use all (or any) of the quantities that end up getting listed, but having that list is a good starting place for the steps that follow.
To illustrate this better, let's use an example: If you laid all the French fries you ate in a year end-to-end, how many city blocks would they stretch? There isn't much information. There isn't even a definite solution, but a good approximation can be made. The place to start is by listing out what pieces of information might be important to the problem. The immediate constituent quantities for this calculation might be the length of one French fry, the length of a city block and the number of French fries you eat in a year. The number of fries you eat in a year could be further broken down into the number of fries in a box, the number of boxes consumed per week and the number of weeks in a year.
Once these quantities are identified, they need to be numerically defined. Some of them are quantities that have known values or can be looked up, like the length of a city block or the number of weeks in a year. Other things that fall into this category are physical constants or easily Google'd measured quantities. Quantities that can't be looked up readily are marked for estimation. This is a departure from the method proposed by Weinstein and Adam, where every quantity should be estimated1, but students always have cell phones with them, so it doesn't make practical sense to deprive them of easily accessible information. Plus, the accepted values lend themselves to discussions about how good their estimates would have been.
The next step is to attend to units. What is the unit on each of these quantities? This becomes an ideal time to dig into the meaning of "per," the standard linguistic signifier of a rate or ratio. What is a mile per hour or a meter per second? How is that similar to some of the units that would pop out of our example question, like boxes per year, fries per box, weeks per year, meter per fry and meter per block? Every quantity has a unit and students should develop the habit of always supplying the unit with computations.
In practice, those first three "steps" happen simultaneously. You can identify the constituent quantity, supply the unit and mark it to be looked up or estimated all at once. Once the list of possible constituent quantities is assembled, they need to be formed into a calculation that results in the desired quantity. Chemistry teachers will recognize this as a process that's functionally identical to stoichiometry, but that prior knowledge isn’t required. The idea is to assemble the constituent quantities in such a way that the extraneous units "cancel," leaving only the final unit and thus the final answer. This somewhat formalizes and somewhat diverges from the (admittedly easily accessible) process outlined by Weinstein and Adam2, but was selected to specifically ground this process in other commonly accepted science practices.
Let's apply this to our example. To estimate the total length, in blocks, of all the French fries I eat in a year, I'm going to need to know the following quantities, with their unit in parenthesis: the number of fries I eat in a year (fries/year), the length of one fry (m/fry) and the length of a city block (m/block). I'll further break down the number of fries per year into the number of fries in an order (fries/order), the number of orders I eat in a month (orders/month) and the number of months in a year (months/year). Since I'm looking for a result in blocks/year, the units could be arranged as such, paying attention to the fact that the reciprocal of the length of a block is used:
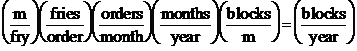
Estimation
Estimation, as a skill, is founded in equal parts on number sense and self confidence. Students need to narrow the order of magnitude, establish a range of reasonable values, pick a central value to represent that range and then be confident enough in the assumptions they've made for their estimation that they feel comfortable leaning on it in a calculation. Making this work for students requires that they develop advanced number sense with special emphasis on orders of magnitude and precision.
Orders of magnitude, or powers of ten, is a term used to describe the dominant place value in a quantity and by how many decimal places two quantities differ. We operationally know that adding a zero to the end of a number makes it ten times bigger, but it's often hard to imagine what that might look like. Learning and developing estimation techniques can help bring us closer to a more intuitive understanding of orders of magnitude, because they are the fastest way to pinpoint quantities on a spectrum of values.
To apply to our previous example, let's try to find the order of magnitude for each of the quantities we'll have to estimate and see how that begins to shape our answer. These extremely rough estimates will be refined later, but just trying to pin the result down within an order of magnitude is a strong way to begin estimating. A French fry is probably a single digit number of centimeters, so we have a number on the order of 0.01 m, or 10-2 m/fry. An order of fries doesn't have hundreds of fries in it. And a box doesn't have a single digit number of fries; it has tens of fries. So we're looking at 101 fries/order. I don't eat fries more than ten times a month, so we have 100 orders/month. Months per year is tricky. We know there are 12 months in a year, but we’re not looking to be that precise yet. Twelve is on the order of 101 and the unit is months/year. In Philadelphia, a city block is a little longer than a football field, so there are on the order of 102 m/block, which translates to 10-2 blocks/m. Let's put that together and narrow down our answer.

Once students are comfortable with making these order of magnitude estimates for individual quantities, they need to be reflected upon and refined. The initial result of 10-2 blocks per year seems small. Does it make sense? When I look back, one French fry is probably much closer to ten centimeters than one. There are definitely more than ten fries in a box, but not 100. I eat fries more than once a month. There's 20% more than ten months in a year, but there are slightly less than 10-2 blocks/meter. All combined, this reinforces the initial notion that the order of magnitude estimate was too small. Now that we have an understanding of our computation, we’re in a position to refine it.
Before that happens, now is the time to address matters of precision. Science classes push the use of significant figures, and rightfully so. The stumbling block is that students view them as a set of rules as opposed to the natural extension of the relationship between measurement and estimation that they are. Digits are significant when you're sure of their quality and typically you're entitled to estimate one digit. Let's say I need to measure a piece of wood. I can use a meter stick, that has mm markings or I can use my thumb, which is about 2 cm wide. Both methods should give me the same order of magnitude, say tens of centimeters or hundreds of centimeters, and probably even the same leading digit. After that, they'll likely diverge, because the level of allowed precision is intrinsic to the measuring device used – this is the purpose of the scientific practice of using significant figures. The meter stick allows me to be sure of millimeters. My thumb requires me to estimate the number of centimeters. Looking at significant figures then becomes a way to quickly evaluate the quality of a measurement or calculation, but also a way to keep computation honest. A calculation is only as good as the worst measurement, so if one value could be off by up to 50% in either direction, your result could be off by up to 50% in either direction. Better measurements yield higher precision and that precision is manifested in more significant figures.
How is an estimate made? A good technique to use is to start by setting reasonable boundaries and then pick a number in between. Students will gravitate toward taking the average, or mean, but that's a construct more suited to situations involving addition and subtraction, rather than for the order of magnitude estimates and multiplicative constructions inherent to this type of problem. A more appropriate tool is the geometric mean, which we can think of as a multiplicative average. First let’s look at the formula for arithmetic mean (AM) between two numbers, a and b:

The geometric mean (GM) between a and b is found by “escalating” that calculation. Instead of adding a and b, they are multiplied. Instead of multiplying by one half, their product is raised to the one half power, which is the square root:
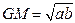
For an arithmetic mean, if you add or subtract the same value from the central point, you get to the bounds; it represents the additive midpoint between the two numbers. For the geometric mean, if you multiply or divide the central point by the same value, you arrive at the bounds. This gives you a multiplicative midpoint, analogous to the function of the arithmetic mean. Another way to look at this is if you add the two original numbers, you get the same answer as when you add the arithmetic means to itself; and when you multiply the two original numbers, you get the same answer as when you multiply the geometric mean by itself.
It’s also interesting to note that in all cases, except for where a=b, the arithmetic mean is always larger than the geometric mean. In the case where a=b, the arithmetic mean and the geometric mean are equal, and AM = GM = a = b.
Let's compare the arithmetic and geometric means between 1 and 100. From above, the arithmetic mean is computed by adding the bounds and dividing by two:
(1+100)/2 = 50.5
If 49.5 is subtracted from or added to the arithmetic mean of 50.5, the bounds of 1 and 100 are recovered. Thus, 50.5 represents the number midway between 1 and 100.
Contrast this with the geometric mean. From above, the geometric mean is computed by multiplying the two bounds (instead of adding) and then taking the square root (instead of dividing by two). Therefore:
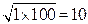
If the geometric mean is divided by ten, you recover the lower bound. If it is multiplied by ten, the upper bound is recovered. Similar to above, 10 is “midway” between 1 and 100, but in a multiplicative, not additive, sense.
When performing estimates, feel entitled to one digit and an order of magnitude. Anything more precise than that is a lie. Getting my students to internalize this idea and not report results with much higher precision will be a struggle, because they view every digit that pops up in a calculator as equally important, a misconception that we debunked in the rationale for this unit.
One example in the trap of false precision comes in estimating the radius of the Earth in miles and then converting that to kilometers. The average radius of the Earth is around 4000 miles, a number that has to come with a fair amount of qualification, seeing as the Earth is bulgy around the equator, not a sphere. The Earth also has tall mountains and vast undersea trenches, and therefore can’t be considered a smooth object. The conversion factor between miles and kilometers is known to very high precision: there are 1.609344 kilometers in one mile. So let’s find the average radius of the Earth in km.
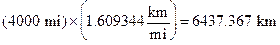
Wait, what just happened? Just because we converted the units doesn’t mean we made a better measurement! Even though the conversion factor is extremely precise, we’re still only entitled to the significant digits we started with. 4000 mi is good to two significant figures (maybe even better, despite the roundness of the number), so we can round our conversion to a more reasonable 6400 km. Students have a natural inclination to view unit conversions as perfect operations, but still remind them to attend to allowable precision.
When students are unsatisfied with their single significant digit and an order of magnitude, we need to remind them that precision isn't the point of every calculation. They're going to be setting themselves up to verify a more complex future calculation, ballpark a new number to put an idea into perspective or judge whether or not a figure someone's quoted seems reasonable. For these purposes, a single significant digit is perfect. Stress to your students that they're trying to understand the world better, not build a bridge. No one is in danger of dying if they're off by a factor of two, but they can learn a great deal if they're within a factor of ten.
The other desired effect of getting students away from reporting meaningless digits is an increased understanding of place value and relative accuracy. How often have you run into a situation where you tell students that an answer is “around 2000,” and someone shoots their hand straight up into the air? I can already predict what they’re going to say. Probably, “I got 2031.8, is that okay?” Normally I’d respond with, “Calculate the percent difference and tell me how you feel about that,” but I’d like to illustrate the point with an example.
Think about the square root of two. I'd probably write down 1.4 or 1.41 off the top of my head, depending on the situation and what I was trying to do. Ask a student, however, and you'll probably see them scribble down 1.414213562... until they run out of digits on their calculator display. They don't have a sense of how meaningful each digit is. Not all ones are created equal! Look back at that "student response." The leading 1 represents over 70% of the actual quantity being expressed. That second one, just two decimal places away, represents less than 1%. And that third one, three more decimal places away, is less than 0.001%.
Another good exercise can come from modeling the Earth as a perfect sphere and calculating the surface area. Looking up the mean Earth radius gives a value of 6371 km (which doesn’t even make sense to ±1 km, for the reasoning above), but let's use successively more precise values for the radius and perform the calculation, given that the surface area of a sphere is 4πr2:
4π(6 x 103km)2 = 5 x 108km2
4π(6.4 x 103km)2 = 5.1 x 108km2
4π(6.37 x 103km)2 = 5.10 x 108km2
4π(6.371 x 103km)2 = 5.101 x 108km2
The difference between the least precise result and the second least precise result is 2%. The difference between the two most precise results is 0.02% and the most precise result doesn't impart any additional insight, especially when you consider all of the complicating factors that were brushed over to arrive at these answers in the first place. When students do this process for other calculations and compare the percent difference, they should start to realize almost all of the value in the calculation is in the first digit. The second can modify the answer somewhat but past that, the differences are inconsequential. It’s also worth noting that when you round a number between 10 and 20 to the nearest 10, the percentage error may be much larger than when rounding a number with a leading digit greater than one.
With this understanding of reasonable and relative precision and the tool of geometric mean, let’s refine the estimates we made for our French fry problem. A typical French fry is between 6 and 10 cm. There are somewhere between 30 and 100 French fries in a typical order. I eat French fries somewhere between two and 8 times per month and a city block is between 100 and 200 meters. 12 months in a year is a known quantity, so we’ll use that. Let’s compute the geometric means and keep only one significant digit:
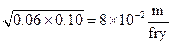
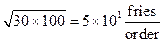
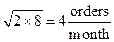
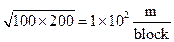
The calculation now becomes:

Two blocks per year is, as suspected, significantly larger than what we had before and much closer to my gut feeling. It’s also somewhat depressing and makes me seriously question my dietary choices. But, the calculation did its job. It provided perspective and insight, both into the problem solving process and the scenario we considered.
Justification
The final piece of the puzzle is being able to justify and explain what’s been done. If you’ll notice, during the estimation phase I made some assertions that you may or may not have agreed with. The most controversial is probably about the size of city blocks. The justification I’d use for my estimate is that since I’m from Philadelphia, I’m talking about Philadelphia city blocks, which are different than New York or Chicago city blocks. I also eat French fries probably once per week. By clarifying the assumptions that led me to the estimates that I made, I’ve showed two things: First, that my end result should be reasonable if you agree with the assumptions I made in the estimations. Second, that I’ve considered the numbers that I’m writing down instead of just pulling them out of thin air.
Under the Common Core, the justification skills that go into backing up an estimate are easily assessed under the Argumentative Writing rubric. Students should be providing evidence for what they do and considering alternate positions. Obviously there won’t be a sustained narrative surrounding the solution to a Fermi problem, but students should be able to explain their rationale and calculations to other students in either a paragraph or short presentation. Requiring students to explain their work with more depth than just listing the steps they followed will force them to be more meticulous about how they consider their work at all steps of the process. It also helps me assess their work and provide specific feedback by making clear the logic and rationale behind each step.

Comments: