Teaching Strategies
Using an example problem has allowed me to break the process down for clarity of exposition, but this is not the way I will present it to my students. Some suggestions are provided for illustration, but they are not exhaustive. The classroom activities are presented as skill building activities first. The skills will first be developed in isolation and then built into multi step problem solving through a process of careful scaffolding. Here I’ll assemble some strategies that guide my selection of classroom activities to build order of magnitude sense, justified estimation, dimensional analysis and problem decomposition. In the next section, I’ll outline specific activities I’ll use with each of these strategies. Refer to the appendix for additional problems that are aligned with each topic.
Orders of Magnitude and Estimation
I plan on teaching estimation by teaching two different techniques. Students will start doing one-step estimations, or working with quantities they can estimate directly. The first, order of magnitude estimation, requires pinning down a result within a factor of ten. I will be sure to be clear with my students about what they’re trying to do, which is pick a power of ten that is closest to the true value of the quantity they’re trying to estimate. Think about a bag of Swedish Fish (my favorite candy!). What order of magnitude goes with the number of fish in a small personal-sized bag? There are tens of fish in there, but not 100, so the estimate would be on the order of 101 fish. How about the thickness of a penny in meters? It seems to be around a millimeter or two, so it would be on the order of 10-3 meters. I will stress to them that they’re just trying to find the power of ten that would go with the real amount.
After some practice with nailing down orders of magnitude, tougher estimates can get much better through a technique known as bounding. The idea is to specify reasonable upper and lower bounds for the quantity you want to estimate and then pick a number somewhere in between. To present the idea to my students, I’ll have them pick a number that they know is too small (lower bound) and a number they know is too big (upper bound). Then, looking at these boundaries, I want to ask them to try and “squeeze” them down. As an example, let’s consider the circumference of the Earth in miles. You could be extremely conservative and say it’s more than one mile and less than one million miles, and you’d be right, but we can move those bounds in by quite a bit. The distance from New York to Los Angeles is about 3000 mi, so that’ll be our new lower bound. For some reason I always remember that the distance from the Earth to the Moon is around a quarter of a million miles, so that can be our new upper bound. This gives us a range less than one-fourth our original, so we’re making progress! With some clever thinking about time zones, we could narrow that down even more, but let’s say one of my students stalls out there. How might I help them pick a number somewhere in between?
Assuming they did an order of magnitude estimate (and know the distance between NYC and LA), they probably guessed that it’s on the order of 104 mi for a whole trip around the Earth. When picking a number “in the middle” of two other numbers, my students will automatically default to taking the average, or arithmetic mean, which yields a number on the order of 105 in this case. I want to make them feel unsettled about this, because it doesn’t fit with what they know, so it must be reevaluated! For estimates like this and situations where they’ll be multiplying a number of estimates together, finding a multiplicative average, or geometric mean, is preferable. They can of this as the multiplicative analog of the arithmetic mean. I don’t want to make this concept more intimidating than it needs to be for my students. They remember that the arithmetic mean between two numbers involves adding the numbers and then dividing by two. For the geometric mean, adding the two numbers becomes multiplication. Division by two is replaced by the square root.
In general, I want them to know that the geometric mean between lower bound a and upper bound b is:
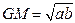
So for our example:
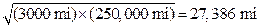
Then, I want to demonstrate to them that multiplying (not adding) the lower bound by a certain number gets us to the geometric mean. Multiplying the mean by that number gets us to the upper bound.
30 x 9.13 ≈ 27,386
27,386 x 9.13 ≈ 250,000
And in general:


In keeping with our earlier talks about precision, our result from using the geometric mean to estimate the circumference of the Earth is far more precise than we have any business being, so let’s round that result to one decimal place. This gives a result of 3 x 104mi, consistent with the order of magnitude estimate and within 20% of the frequently used value of 25,000 mi for Earth’s equatorial circumference.
Learning to be a good estimator comes with practice, because estimates are usually better when you have a known quantity in mind to compare them to. Both of these are reasons why all the warm-ups I’ll do during this unit will be quick estimation tasks. Future estimates can build on past estimates, or students can even perform estimates on the way to the final estimate. I require them to specify the upper and lower bounds and the rationale for their result. When they’re done, they will calculate a percent difference, as this can often put numbers that “feel” far apart into better perspective. I’m very visual with data for my classes, so I’ll make histograms for the class and bin their estimates based on percent difference. That way, the students can chart how much their skills are improving over time. Plus I get to teach them how to use histograms, so it’s a double win.
Dimensional Analysis and Unit Conversion
My class benefits from every student having taken chemistry the year prior, because the unit conversion process that I teach looks an awful lot like stoichiometry. The basic idea of the process is that if we place equivalent quantities in different units in the numerator and denominator of a fraction, the value of the entire fraction is one. Then, when a quantity is multiplied by one, its value doesn’t change. This allows the units of a quantity to change while the total amount expressed remains the same. As a one step unit conversion, I might ask my class to express 450 feet in meters. One meter is close to 3.28 feet, so we set up a conversion factor, in the form of a fraction, and complete the calculation:
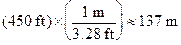
What students should see is that the unit of feet appears in both the numerator and denominator, so it “cancels,” leaving a unit of meters. This is a one step conversion, because it requires one conversion factor. As a two-step conversion, I might ask: Not counting the end zones, how many rods is a football field? Football fields are expressed in yards, one rod is 16.5 feet, so they’ll also need to convert yards to feet so everything lines up:

I want them to see that yards appears in the numerator of the first quantity and the denominator of the first conversion factor. Feet appears in the numerator of the first conversion factor and the denominator of the second. Finally, rods, the remaining unit appears in the numerator of the final conversion factor, making it the unit of the result. I’ll point out to students that units that they don’t want to appear in their answer need to show up in both the numerator and denominator of the original quantity or conversion factors. The power of this technique is that it works just as well with exotic as with mundane units and will serve as the framework for the problem decomposition and solving techniques. Additionally, units never cease to be important. In a physics class, I always think it’s a great idea to have my students perform this process, known as dimensional analysis, on the equations they’re using to make sure they’re getting the answers they want in the units they require.
Another way I want to tie unit conversion back to precision is to have my students evaluate approximate conversions in order to simplify them. Conversion factors are well known and easily looked up, but to my students they feel very carved in stone. I want to ask them what percentage error is involved in saying one foot is equal to 30 cm? Or that one mi/h is equal to 1.5 ft./s? Or that one year is π x 107 s? Then, in what sorts of situations is the approximate conversion good enough? These sorts of questions will fit well into an introductory homework assignment or as a few warm-ups when they first come into my class. The end goal is to help my students get a better feel for how different units relate to each other on an intuitive level, so they can get develop an increased fluency in approximately equating different quantities and expressing their estimates.
Problem Decomposition
When addressing problem decomposition, I steadily keep in mind that I am building students toward the end goal of performing multistep estimates on their own. I have students identify what they’re looking for and the unit. Then, I like to have them make a list of any constituent quantities that might help them solve the problem, along with the appropriate units. At this point, it doesn’t matter if they list quantities they won’t actually need. My students will be started with “one step” decompositions, or questions that split once, cleanly into two parts. As an example, let’s examine a one step question: What is the weight of a bathtub full of water in kilograms?
The question specifies units, so we’re looking for an answer in kilograms per bathtub. We’ll probably need the density of water (kg/L) and the number of liters in a bathtub. (L/bathtub). Students might want other information, like the number of cups in a gallon or the temperature of the water, but when the calculation is arranged, it should become apparent that the units of these other quantities don’t fit. Let’s construct the skeleton of the calculation that gets us to our result:
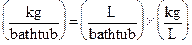
Notice that kg was in the numerator of our answer, so the constituent quantity with kilograms was arranged so that kg was in the numerator. The same attention was paid to “bathtub,” which needed to appear in the denominator. We picked our constituent quantities well, so that liters appeared in both numerator and denominator, but if it didn’t, we could have added more constituent quantities or conversion factors to get the other units to cancel each other out. From here, the computation is trivial, because we can just put in values for the capacity of the bathtub and the density of water. An average bathtub holds around 150 L of water, so the calculation becomes:

That’s over 300 lbs. of just water in a bathtub!
Let’s now apply this to the multi step question of how many miles a person walks in a lifetime. The answer should be in miles per lifetime. The constituent quantities might include how long a person lives (years per lifetime), how much time a person spends walking in a normal day (hours per day) and how fast a person walks (miles per hour). Notice that this doesn’t quite work out:

Lifetime and miles appear where they should and hours appears in both the numerator and the denominator, but years and day are left. What we can use is a conversion factor, with days in the numerator and years in the denominator, to make sure the units agree.
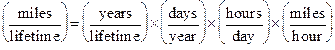
It’s also important to note that this isn’t the only way to get to a valid answer. Someone in my class might argue that it makes more sense to estimate how many miles you walk in a day directly or that a person’s walking speed is nowhere near a steady pace. Beyond that, the results will vary pretty substantially from person to person. The beauty of this type of problem is that different approaches and results are expected, as long as the thought process is justified.
To implement this in my class, I will start with an example or two that we handle together. I’ll ask students what they might need to know in order to answer the question and compile the list on the board, being sure to pause and ask for units. Then I’ll reference the unit conversion procedure with students for guidance on how to arrange the units to set up the calculation skeleton. After each calculation is set up, students will estimate (or look up) the values of each piece and complete the calculation as a group. Starting them with the one-step examples, I’ll work them up to more complex questions that add more quantities. My main focus here is making sure they are attending to all of the skills and necessary justification that they’d developed along the way.

Comments: