Teaching Approach
Number Talks
For this and the preceding unit, the content will all be delivered in some variation of a number talk. This is a routine that will last five to ten minutes at the start of a class period. The strategy follows a basic format of presenting a prompt, allowing time for students to think, soliciting solutions, and finally discussing the rationale behind the offered solutions and coming to conclusions as a class. It should be noted that number talks are more typically done with prompts that cover general computational and mental math strategies. The prompts given in this unit will have the narrower focus of representing and interpreting adding and subtracting rational numbers via the number line. These talks will serve the purpose of eliciting different ways of making sense of number concepts, require students to justify their ideas using sound reasoning, and help each other reach better understanding through student led discourse. These prompts will vary in their delivery in terms of what is given and what is being asked, but will have the aim of making sense of various representations of adding and subtracting rational numbers.
Presentation of Prompts
Throughout the unit, I will show my students a variety of different prompts to elicit discussion around the desired content for that particular day. The majority of prompts will be projected at the front of the room. Students will respond on paper where there will be blank number lines for students to answer the prompt and explain their thinking. For certain number talks I will provide parallel practice prompts below so that students can practice and master a given concept after the whole group discussion. It will be important to provide students standard number lines to make sure the intervals are accurate. When students are familiar with salient structures of the number lines, I will then encourage them to create their own number lines to respond to prompts. Their written work will be stored in student portfolios so that students can keep track of their learning and refer back to notes throughout the unit.
I expect the entire unit to last 5 to 6 weeks depending on how quickly students demonstrate mastery of the concepts. In total, this unit and the prerequisite unit should last 10 to 12 weeks. Upon completion of the two units, we will consider more advanced number concepts on the number line including multiplication, division, and irrational numbers.
Prompts will vary by including or excluding certain information on the number line and by asking students to perform different tasks. For a complete set of prompts and other lesson materials that will be used for this unit see Appendix 2 for the website to visit. Below is a description of the types of prompts that will be given to teach various concepts.

Figure 13
Figure 13 prompts students to “do” something with the vectors in order to represent the sum of two quantities. First students must figure what each vector represents by using the number line to measure while attending to the vector orientation. The question is purposefully vague to allow students the opportunity to discuss different ways of seeing the sum as positive 1.
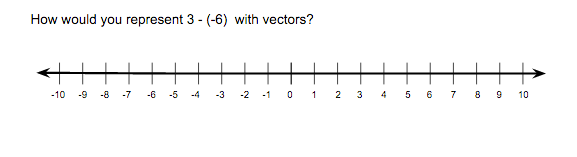
Figure 14
Figure 14 is an extension of the prompt in figure 13. Here students will attempt to draw the vectors on the number line independently. From here students will discuss how they represented each part of the expression. This task requires students take each part of the expression and visualize what is implied, bringing the abstract into the context of the number line.
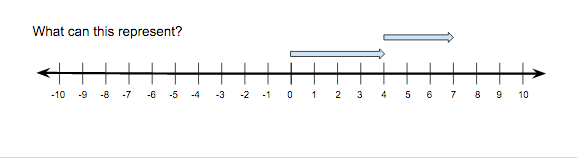
Figure 15
Figure 15 requires students to do the reverse task presented in figure 14. It is important to note that the question encourages more than one answer by asking: What can this represent? Students should see that the representation could either show 4 + 3 or 4 – (-3). This type of prompt should also be used to highlight the connection between adding and subtracting the negative.

Figure 16
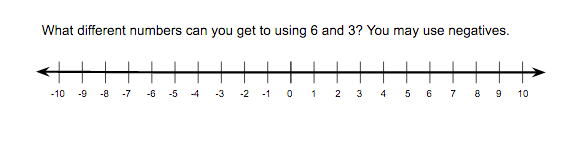
Figure 17
Figures 16 and 17 give students the task of experimenting by using different combinations of numbers to add and subtract. The value of this prompt is that it allows for multiple solutions and provides opportunities for students to see the impact of adding and subtracting negatives or positives. With multiple prompts of these and similar types, I will push students to generalize and find the total number of possibilities for each situation.
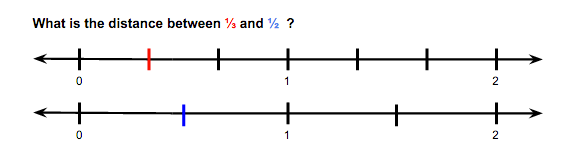
Figure 18
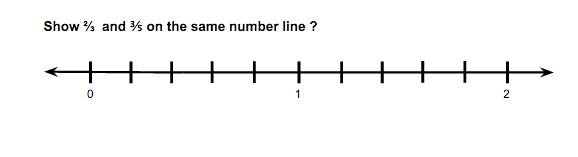
Figure 19
In Figures 18 and 19 students are prompted to grapple with different fraction concepts. In order to answer each question, students will have to manipulate the given number line by adding new interval marks. To answer this prompt they must address the equal subdivision of a unit in order to determine distance.
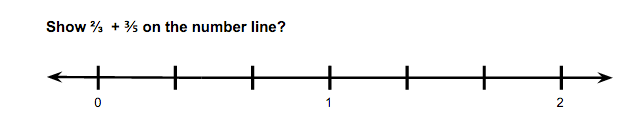
Figure 20
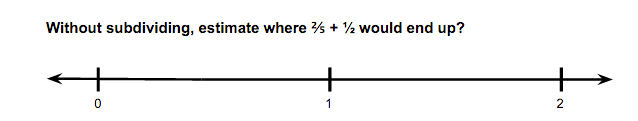
Figure 21
Figures 20 and 21 get students to visualize operating with rational numbers. Figure 20 encourages students to complete the more formal process of renaming fractions in order to find a common denominator before adding. While Figure 21 requires students to estimate and use their knowledge of fractions on the number line to find a sum. In figure 21 it will be important to prompt students to justify why they chose their placement on the number line.

Comments: