Linear Measurement
Students first see numbers as counting numbers and then generally next as linear measurement. The key features of a number line are that it has:
1) order, and
2) distance
A next step to turning a line into a number line, known as coordinatization, you must:
1) choose an origin,
2) choose unit distance a positive direction,
3) label other points with the number that as the ratio of the distance of the point to zero, + if it is in the same direction, - if in the other direction.
Which all explains the Measurement principle: the number labeling a point on the number line tells you the distance of that point from 0, the origin, as a multiple of the unit distance.
Because second grade in many ways continues the first grade mathematics learning, it is important to continue to focus on the Three Pillars listed above. This unit focuses particularly on the third pillar: Making Connections Between Counting Number and Measurement Number, specifically linear measurement. Linear measurement, the measurement of length or distance, would probably be considered the most basic and the simplest types of measurement. A ruler is what we often think of when considering linear measurement. Young students should use a variety of manipulatives to work with and practice this concept, connecting cubes, rods and cubes. This is an important time and step to take with students as they begin to think about length or distance using counting numbers.
Rods and cubes are a basic mathematics materials used by students in early grades. Interlocking cubes can be made into trains to show a number and a length. Unifix cubes are one type but any connecting cubes of that are of the same size and come in different colors would serve the same purpose. Students will readily see that although the composition of a number changes, the total number of cubes remains the same and, important to emphasize, the length also remains the same. Using the bar length of 6 as an example for how students can use this strategy to gain understanding. The use of the length model for addition shows all the ways of decomposing a number into a sum, by showing a bar length of 6 above bars of lengths 1 and 5, above bars of lengths 2 and 4, above bars of lengths 3 and 3, above bars of lengths 4 and 2, above bars of lengths 5 and 1.
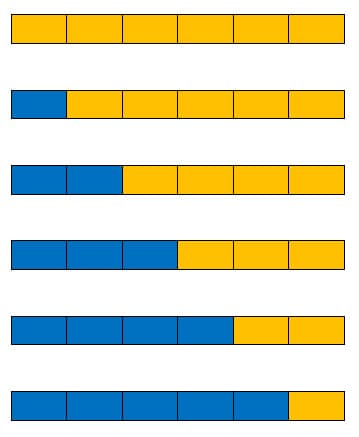
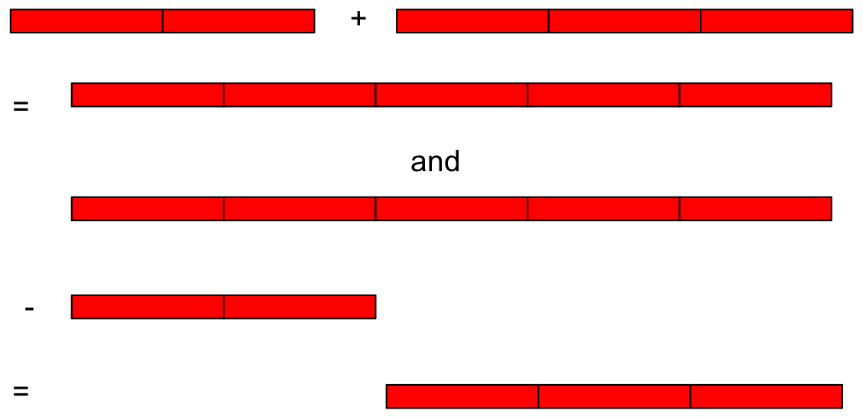
Cuisenaire rods are a set of 10 colored rods ranging in lengths from one unit to ten. They are useful in this unit for students to investigate and practice combining and comparing lengths, pre-numerical addition and subtraction. They will notice that some collection of the rods, when placed end-to-end, can match a length of another set of rods placed end to end. With guidance, students can learn that one of the rods, likely the smallest which is actually a cube, can become the designated unit. This can be used to measure the other rods to determine the number of small rods make up the longer rod. This number is the length of that rod. Students will begin to realize that the length of the rod made by placing two rods end to end is the sum of the lengths of the individual rods. Lengths can also be subtracted by comparing the rods. By putting the rods side by side, only end lined up and then measuring to "extra" length of the longer rod as compared to the shorter rod, students will find the difference.
Example of 2 + 3 = 5, and 5 - 2 = 3
Other ways for students to practice linear measurement could include activities such as using a pencil to see how many it takes to equal the desk top, the chalk board or other choices around the classroom. As they become good at this idea, connecting length and number and practice joining rods end to end, they are taking the step toward having a concrete understanding of how the base ten structure of our base ten system works.
Base ten blocks can be introduced, with each cube representing 1and rods of length 10 representing 10. These pieces can be assembled to represent any two-digit number. To add together two-digit numbers, the 10 rods and cubes can be lined up in trains arranged in the standard arrangement, 10-rods on the left and cubes on the right. Once they are in place, the blocks can be rearranged to show that the numbers are decomposed into their base ten components and added, the recombined.
21 + 34 = (20 + 1) + (30 + 4)
= 20 + (1 + (30 + 4)) = 20 + ((1 + 30) + 4) = 20 + ((30 + 1) + 4) = 20 + (30 + (1 + 4))
= (20 + 30) + (1 + 4) = 50 + 5 = 55
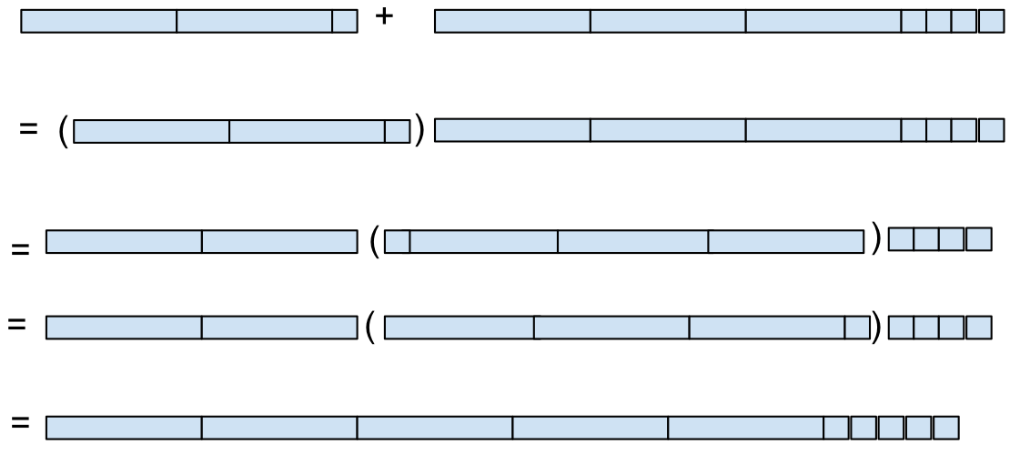
This example shows that first we put the trains together and see the length combined. Then we notice that the one-cube from the first addend and the ten rods from the second addend are in the wrong places or order. Using the Commutative property, reverse the order of the one-cubes and ten-rods. Now the trains are one long length and looked at as a whole.
After this practice, combining two-digit numbers, students can work with three digit numbers to perform the same process. To simplify management, 100 flats are formed as a square which cannot convey the sense of length when three-digit numbers are combined. Showing the length by using rods would demonstrate how much larger 100 is in length to 10, and similarly, although not easily done, a 1000 rod would provide an indication of magnitude that a thousand cube does not. For this more dramatic visual, the use of the school hallway, and likely some borrowed materials, can allow enough room for the 1000 length to be seen. The differences in length when moving from 2-digit numbers to 3-digit and finally to 4-digit numbers will be quite evident!

Comments: