The Number Line
As defined above, the basic principle that determines a number line is:
The number that labels a point tells the distance of that point from the origin (the endpoint), as a multiple of the unit length.
Students in first and second grade will be using what is called the number ray which is the positive half of the number line. It of course is essentially a ruler with the zero point, or origin, at one end and extending in the positive (right) direction.

With the introduction of the number line, bars of various lengths, such as the Cuisenaire rods, can be used to show the connection of counting to length. The unit length of the rods will be equal to the unit length on the number line. This practice will demonstrate visually that the numbers on a number line are describing distances. Numbers on the number line are often referred to as points on the number line. Points do not provide meanings for adding and subtracting. How can you add one point and another point and get a third point? This is only possible if the points are actually end-points of distances from zero created by length.3
Our brains seem to be wired to see things, not lengths. This makes seeing length/distance on the number line difficult. Because of this visual difficulty for students (and others), the National Research Council reports conclude that number line are not appropriate for PK, K or even grade 1. The CCSSM is consistent with these recommendations, first introducing the number lines in grade 2.
As mentioned before, rulers has the same structure as a number line. One strategy to help students see and use the distances is to have them draw one unit length and write a 1 after it, then very close below draw a two length units with a 2 after it, then three length units followed by a 3, and so on. They can think of a ruler as all of these lengths pushed together to make a single line with all of these lengths on it; the number of lengths so far is noted at the end-point of each length.
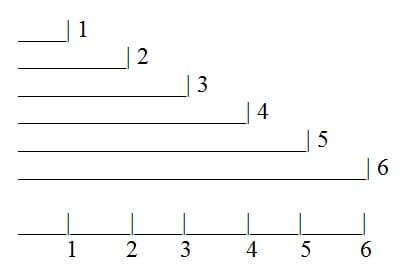
Visual models are one of the central core ideas and practices of the CCSSM. Research shows that simple math drawings that students can make and use in their own way in problem solving and explaining of thinking increases and improves their understanding.4

Comments: